Kaj je Krožni povezani seznam?
The krožno povezan seznam je povezan seznam, kjer so vsa vozlišča povezana v krog. V krožnem povezanem seznamu sta prvo vozlišče in zadnje vozlišče med seboj povezana, kar tvori krog. Na koncu ni NULL.
Krožni povezani seznam
Na splošno obstajata dve vrsti krožnih povezanih seznamov:
- Krožni enojno povezani seznam: V krožnem posamično povezanem seznamu zadnje vozlišče seznama vsebuje kazalec na prvo vozlišče seznama. Prečkamo krožni enojno povezan seznam, dokler ne dosežemo istega vozlišča, kjer smo začeli. Krožni enojno povezani seznam nima začetka ali konca. V naslednjem delu katerega koli od vozlišč ni ničelne vrednosti.
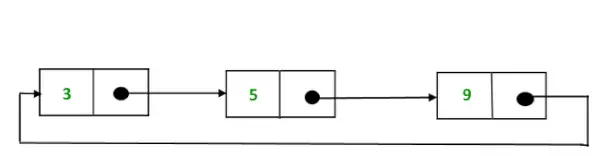
Predstavitev krožnega enojno povezanega seznama
- Krožni dvojno povezani seznam: Krožni dvojno povezani seznam ima lastnosti dvojno povezanega seznama in krožnega povezanega seznama, v katerem sta dva zaporedna elementa povezana ali povezana s prejšnjim in naslednjim kazalcem, zadnje vozlišče pa kaže na prvo vozlišče naslednjega kazalca in tudi prvo vozlišče kaže na zadnje vozlišče s prejšnjim kazalcem.
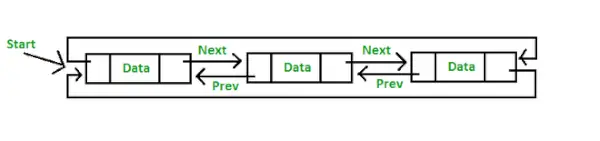
Predstavitev krožnega dvojno povezanega seznama
Opomba: Za predstavitev delovanja krožnega povezanega seznama bomo uporabili posamično krožno povezan seznam.
Predstavitev krožnega povezanega seznama:
Krožni povezani seznami so podobni enojnim povezanim seznamom z izjemo povezovanja zadnjega vozlišča s prvim vozliščem.
Predstavitev vozlišča krožnega povezanega seznama:
C++ // Class Node, similar to the linked list class Node{ int value; // Points to the next node. Node next; }> C struct Node { int data; struct Node *next; };> Java public class Node { int data; Node next; public Node(int data) { this.data = data; this.next = null; } }> C# public class Node { public int data; public Node next; public Node(int data) { this.data = data; this.next = null; } }> Javascript class Node { constructor(data) { this.data = data; this.next = null; } }> PHP class Node { public $data; public $next; function __construct($data) { $this->podatki = $podatki; $this->next = null; } }> Python3 # Class Node, similar to the linked list class Node: def __init__(self,data): self.data = data self.next = None>
Primer krožnega enojno povezanega seznama:

Primer krožnega povezanega seznama
Zgornji krožni enojno povezani seznam je lahko predstavljen kot:
C++ // Initialize the Nodes. Node one = new Node(3); Node two = new Node(5); Node three = new Node(9); // Connect nodes one.next = two; two.next = three; three.next = one;>
C Node* one = createNode(3); Node* two = createNode(5); Node* three = createNode(9); // Connect nodes one->naslednji = dva; dva->naslednji = tri; tri->naslednji = ena;>
Java // Define the Node class class Node { int value; Node next; public Node(int value) { this.value = value; } } // Initialize the Nodes. Node one = new Node(3); Node two = new Node(5); Node three = new Node(9); // Connect nodes one.next = two; two.next = three; three.next = one;> C# Node one = new Node(3); Node two = new Node(5); Node three = new Node(9); // Connect nodes one.next = two; two.next = three; three.next = one;>
Javascript let one = new Node(3); let two = new Node(5); let three = new Node(9); // Connect nodes one.next = two; two.next = three; three.next = one;>
PHP $one = new Node(3); $two = new Node(5); $three = new Node(9); // Connect nodes $one->naslednji = $dva; $dva->naslednji = $tri; $tri->naslednji = $ena;>
Python3 # Initialize the Nodes. one = Node(3) two = Node(5) three = Node(9) # Connect nodes one.next = two two.next = three three.next = one>
Pojasnilo: V zgornjem programu ena, dve in tri so vozlišča z vrednostmi 3, 5 in 9, ki so povezana na krožni način kot:
- Za vozlišče ena: Naslednji kazalec shrani naslov vozlišča dva.
- Za vozlišče dve: Naslednji shrani naslov vozlišča tri
- Za vozlišče tri: The Naslednje točke na vozlišče ena.
Operacije na krožnem povezanem seznamu:
Na krožnem povezanem seznamu lahko izvedemo nekaj operacij, podobnih enojno povezanemu seznamu, ki so:
- Vstavljanje
- Izbris
1. Vpis v krožni vezan seznam:
Vozlišče je mogoče dodati na tri načine:
- Vnos na začetek seznama
- Vnos na koncu seznama
- Vstavljanje med vozlišča
1) Vnos na začetek seznama: Če želite vstaviti vozlišče na začetek seznama, sledite tem korakom:
- Ustvarite vozlišče, recimo T.
- Naredi T -> naslednji = zadnji -> naslednji.
- zadnji -> naslednji = T.
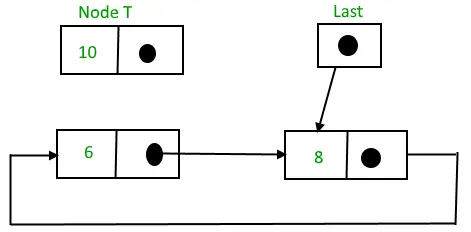
Krožni povezani seznam pred vstavljanjem
In potem,
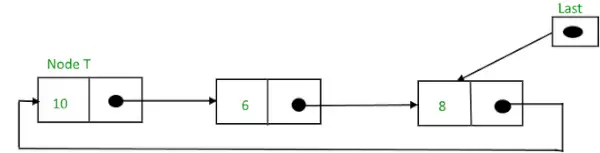
Krožni povezani seznam po vstavitvi
2) Vnos na koncu seznama: Če želite vstaviti vozlišče na konec seznama, sledite tem korakom:
- Ustvarite vozlišče, recimo T.
- Naredi T -> naslednji = zadnji -> naslednji;
- zadnji -> naslednji = T.
- zadnji = T.
Pred vstavitvijo,
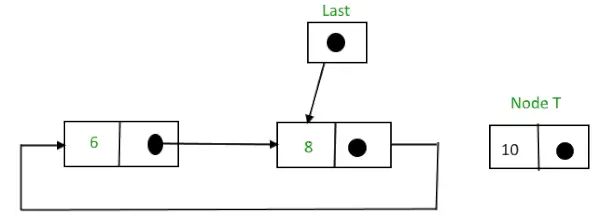
Krožni povezani seznam pred vstavitvijo vozlišča na koncu
Po vstavitvi,
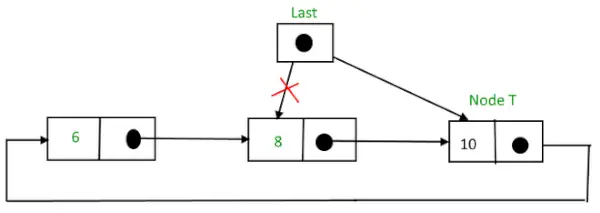
Krožni povezani seznam po vstavitvi vozlišča na koncu
3) Vstavljanje med vozlišča: Če želite vstaviti vozlišče med obe vozlišči, sledite tem korakom:
- Ustvarite vozlišče, recimo T.
- Poiščite vozlišče, za katerim je treba vstaviti T, recimo, da je to vozlišče P.
- Naredi T -> naslednji = P -> naslednji;
- P -> naslednji = T.
Recimo, da je treba 12 vstaviti potem, ko ima vozlišče vrednost 10,
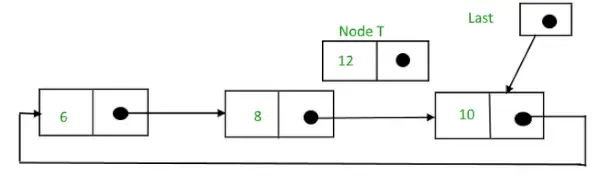
Krožni povezani seznam pred vstavljanjem
Po iskanju in vstavljanju,
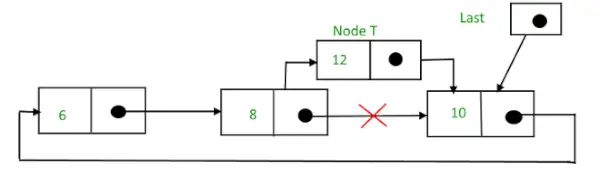
Krožni povezani seznam po vstavitvi
2. Izbris na krožnem povezanem seznamu:
1) Izbrišite vozlišče samo, če je edino vozlišče na krožnem povezanem seznamu:
- Osvobodite pomnilnik vozlišča
- Zadnja vrednost mora biti NULL. Vozlišče vedno kaže na drugo vozlišče, zato dodelitev NULL ni potrebna.
Kot začetno točko lahko nastavite katero koli vozlišče.
Vozlišča se hitro prečkajo od prvega do zadnjega.
2) Izbris zadnjega vozlišča:
- Poiščite vozlišče pred zadnjim vozliščem (naj bo začasno)
- Obdržite naslov vozlišča poleg zadnjega vozlišča v temp
- Izbriši zadnji spomin
- Na koncu dajte temp
3) Izbrišite katero koli vozlišče s krožnega povezanega seznama: Dobili bomo vozlišče in naša naloga je, da to vozlišče izbrišemo s krožnega povezanega seznama.
Algoritem:
Primer 1 : Seznam je prazen.
- Če je seznam prazen, se preprosto vrnemo.
Primer 2 :Seznam ni prazen
- Če seznam ni prazen, definiramo dva kazalca curr in prev in inicializirajte kazalec curr z glavo vozlišče.
- Prečkajte seznam z uporabo curr da poiščete vozlišče, ki ga želite izbrisati, in preden se premaknete na curr na naslednje vozlišče, vsakič nastavite prev = curr.
- Če je vozlišče najdeno, preverite, ali je to edino vozlišče na seznamu. Če da, nastavite head = NULL in free(curr).
- Če ima seznam več kot eno vozlišče, preverite, ali je to prvo vozlišče seznama. Pogoj za preverjanje tega (curr == glava). Če je odgovor pritrdilen, se pomaknite pred, dokler ne doseže zadnjega vozlišča. Ko prev doseže zadnje vozlišče, nastavite head = head -> next in prev -> next = head. Izbriši curr.
- Če curr ni prvo vozlišče, preverimo, ali je zadnje vozlišče na seznamu. Pogoj za preverjanje tega je (curr -> next == head).
- Če je curr zadnje vozlišče. Nastavite prev -> next = head in izbrišite vozlišče curr z free(curr).
- Če vozlišče, ki ga želite izbrisati, ni niti prvo niti zadnje vozlišče, nastavite prev -> next = curr -> next in izbrišite curr.
- Če vozlišča ni na seznamu, vrnite glavo in ne storite ničesar.
Spodaj je izvedba za zgornji pristop:
zbirka javaC++
// C++ program to delete a given key from // linked list. #include using namespace std; // Structure for a node class Node { public: int data; Node* next; }; // Function to insert a node at the // beginning of a Circular linked list void push(Node** head_ref, int data) { // Create a new node and make head // as next of it. Node* ptr1 = new Node(); ptr1->podatki = podatki; ptr1->naslednji = *head_ref; // Če povezani seznam ni NULL, // nastavi naslednje od zadnjega vozlišča if (*head_ref != NULL) { // Poišči vozlišče pred glavo in // posodobi naslednjega. Vozlišče* temp = *head_ref; medtem ko (temp->next != *head_ref) temp = temp->next; temp->naslednji = ptr1; } else // Za prvo vozlišče ptr1->next = ptr1; *head_ref = ptr1; } // Funkcija za tiskanje vozlišč v danem // krožnem povezanem seznamu void printList(Node* head) { Node* temp = head; if (head != NULL) { do { cout<< temp->podatke<< ' '; temp = temp->Naslednji; } medtem ko (temp != glava); } cout<< endl; } // Function to delete a given node // from the list void deleteNode(Node** head, int key) { // If linked list is empty if (*head == NULL) return; // If the list contains only a // single node if ((*head)->podatki == ključ && (*glava)->naslednji == *glava) { brezplačno (*glava); *glava = NULL; vrnitev; } Vozlišče *zadnje = *glava, *d; // Če je treba glavo izbrisati if ((*head)->data == key) { // Najdi zadnje vozlišče seznama while (last->next != *head) last = last->next; // Usmeri zadnje vozlišče na naslednjega // glave, tj. drugega vozlišča // seznama last->next = (*head)->next; brezplačno (*glava); *glava = zadnji->naslednji; vrnitev; } // Bodisi vozlišče, ki ga želite izbrisati, // ni najdeno ali konec seznama // ni dosežen, medtem ko (last->next != *head && last->next->data != key) { last = last ->naprej; } // Če je bilo najdeno vozlišče za brisanje if (last->next->data == key) { d = last->next; zadnji->naslednji = d->naslednji; brezplačno (d); } else cout<< 'Given node is not found in the list!!!
'; } // Driver code int main() { // Initialize lists as empty Node* head = NULL; // Created linked list will be // 2->5->7->8->10 potisk(&glava, 2); potisni(&glava, 5); potisni(&glava, 7); potisni(&glava, 8); potisni(&glava, 10); cout<< 'List Before Deletion: '; printList(head); deleteNode(&head, 7); cout << 'List After Deletion: '; printList(head); return 0; }> C #include #include // Structure for a node struct Node { int data; struct Node* next; }; // Function to insert a node at the // beginning of a Circular linked list void push(struct Node** head_ref, int data) { // Create a new node and make head // as next of it. struct Node* ptr1 = (struct Node*)malloc(sizeof(struct Node)); ptr1->podatki = podatki; ptr1->naslednji = *head_ref; // Če povezani seznam ni NULL, // nastavi naslednje od zadnjega vozlišča if (*head_ref != NULL) { // Poišči vozlišče pred glavo in // posodobi naslednjega. struct Node* temp = *head_ref; medtem ko (temp->next != *head_ref) temp = temp->next; temp->naslednji = ptr1; } else // Za prvo vozlišče ptr1->next = ptr1; *head_ref = ptr1; } // Funkcija za tiskanje vozlišč v danem // krožnem povezanem seznamu void printList(struct Node* head) { struct Node* temp = head; if (head != NULL) { do { printf('%d ', temp->data); temp = temp->naprej; } medtem ko (temp != glava); } printf('
'); } // Funkcija za brisanje danega vozlišča // s seznama void deleteNode(struct Node** head, int key) { // Če je povezan seznam prazen if (*head == NULL) return; // Če seznam vsebuje samo eno // eno vozlišče if ((*head)->data == key && (*head)->next == *head) { free(*head); *glava = NULL; vrnitev; } struct Node *last = *head, *d; // Če je treba glavo izbrisati if ((*head)->data == key) { // Najdi zadnje vozlišče seznama while (last->next != *head) last = last->next; // Usmeri zadnje vozlišče na naslednjega // glave, tj. drugega vozlišča // seznama last->next = (*head)->next; brezplačno (*glava); *glava = zadnji->naslednji; vrnitev; } // Bodisi vozlišče, ki ga želite izbrisati, // ni najdeno ali konec seznama // ni dosežen, medtem ko (last->next != *head && last->next->data != key) { last = last ->naprej; } // Če je bilo najdeno vozlišče za brisanje if (last->next->data == key) { d = last->next; zadnji->naslednji = d->naslednji; brezplačno (d); } else printf('Danega vozlišča ni mogoče najti na seznamu!!!
'); } // Koda gonilnika int main() { // Inicializiraj sezname kot prazne struct Node* head = NULL; // Ustvarjen povezan seznam bo // 2->5->7->8->10 push(&head, 2); potisni(&glava, 5); potisni(&glava, 7); potisni(&glava, 8); potisni(&glava, 10); printf('Seznam pred izbrisom: '); printList(head); deleteNode(&head, 7); printf('Seznam po izbrisu: '); printList(head); vrni 0; }> Java // Java program to delete a given key from // linked list. import java.io.*; import java.util.*; public class GFG { /* structure for a node */ static class Node { int data; Node next; }; /* Function to insert a node at the beginning of a Circular linked list */ static Node push(Node head_ref, int data) { // Create a new node and make head as next // of it. Node ptr1 = new Node(); ptr1.data = data; ptr1.next = head_ref; /* If linked list is not null then set the next of last node */ if (head_ref != null) { // Find the node before head and update // next of it. Node temp = head_ref; while (temp.next != head_ref) temp = temp.next; temp.next = ptr1; } else ptr1.next = ptr1; /*For the first node */ head_ref = ptr1; return head_ref; } /* Function to print nodes in a given circular linked list */ static void printList(Node head) { Node temp = head; if (head != null) { do { System.out.printf('%d ', temp.data); temp = temp.next; } while (temp != head); } System.out.printf('
'); } /* Function to delete a given node from the list */ static Node deleteNode(Node head, int key) { if (head == null) return null; int flag = 0; // Find the required node Node curr = head, prev = new Node(); while (curr.data != key) { if (curr.next == head) { System.out.printf( 'Given node is not found in the list!!!
'); flag = 1; break; } prev = curr; curr = curr.next; } // Check if the element is not present in the list if (flag == 1) return head; // Check if node is only node if (curr == head && curr.next == head) { head = null; return head; } // If more than one node, check if // it is first node if (curr == head) { prev = head; while (prev.next != head) prev = prev.next; head = curr.next; prev.next = head; } // check if node is last node else if (curr.next == head) { prev.next = head; } else { prev.next = curr.next; } return head; } /* Driver code */ public static void main(String args[]) { /* Initialize lists as empty */ Node head = null; /* Created linked list will be 2.5.7.8.10 */ head = push(head, 2); head = push(head, 5); head = push(head, 7); head = push(head, 8); head = push(head, 10); System.out.printf('List Before Deletion: '); printList(head); head = deleteNode(head, 7); System.out.printf('List After Deletion: '); printList(head); } } // This code is contributed by Susobhan Akhuli> C# using System; // Structure for a node public class Node { public int data; public Node next; } // Class for Circular Linked List public class CircularLinkedList { // Function to insert a node at the // beginning of a Circular linked list public static void Push(ref Node head_ref, int data) { // Create a new node and make head // as next of it. Node ptr1 = new Node(); ptr1.data = data; ptr1.next = head_ref; // If linked list is not NULL then // set the next of last node if (head_ref != null) { // Find the node before head and // update next of it. Node temp = head_ref; while (temp.next != head_ref) temp = temp.next; temp.next = ptr1; } else // For the first node ptr1.next = ptr1; head_ref = ptr1; } // Function to print nodes in a given // circular linked list public static void PrintList(Node head) { Node temp = head; if (head != null) { do { Console.Write(temp.data + ' '); temp = temp.next; } while (temp != head); } Console.WriteLine(); } // Function to delete a given node // from the list public static void DeleteNode(ref Node head, int key) { // If linked list is empty if (head == null) return; // If the list contains only a // single node if (head.data == key && head.next == head) { head = null; return; } Node last = head, d; // If head is to be deleted if (head.data == key) { // Find the last node of the list while (last.next != head) last = last.next; // Point last node to the next of // head i.e. the second node // of the list last.next = head.next; head = last.next; return; } // Either the node to be deleted is // not found or the end of list // is not reached while (last.next != head && last.next.data != key) { last = last.next; } // If node to be deleted was found if (last.next.data == key) { d = last.next; last.next = d.next; } else Console.WriteLine( 'Given node is not found in the list!!!'); } // Driver code public static void Main() { // Initialize lists as empty Node head = null; // Created linked list will be // 2->5->7->8->10 Potisni (ref. glava, 2); Push(ref glava, 5); Push(ref glava, 7); Push(ref glava, 8); Push(ref glava, 10); Console.Write('Seznam pred izbrisom: '); PrintList(head); DeleteNode(ref head, 7); Console.Write('Seznam po izbrisu: '); PrintList(head); } }> Javascript // Javascript program to delete a given key from linked list. // Structure for a node class Node { constructor() { this.data; this.next; } } // Function to insert a node at the // beginning of a Circular linked list function push(head, data) { // Create a new node and make head // as next of it. var ptr1 = new Node(); ptr1.data = data; ptr1.next = head; // If linked list is not NULL then // set the next of last node if (head != null) { // Find the node before head and // update next of it. let temp = head; while (temp.next != head) temp = temp.next; temp.next = ptr1; } // For the first node else ptr1.next = ptr1; head = ptr1; return head; } // Function to print nodes in a given // circular linked list function printList(head) { let tempp = head; if (head != null) { do { console.log(tempp.data); tempp = tempp.next; } while (tempp != head); } } // Function to delete a given node // from the list function deleteNode(head, key) { // If linked list is empty if (head == null) return; // If the list contains only a // single node if (head.data == key && head.next == head) { head = null; return; } let last = head; // If head is to be deleted if (head.data == key) { // Find the last node of the list while (last.next != head) last = last.next; // Point last node to the next of // head i.e. the second node // of the list last.next = head.next; head = last.next; return; } // Either the node to be deleted is // not found or the end of list // is not reached while (last.next != head && last.next.data != key) { last = last.next; } // If node to be deleted was found if (last.next.data == key) { d = last.next; last.next = d.next; d = null; } else console.log('Given node is not found in the list!!!'); } // Driver code // Initialize lists as empty head = null; // Created linked list will be // 2->5->7->8->10 glava = potisk(glava, 2); glava = potisni(glava, 5); glava = potisni(glava, 7); glava = potisni(glava, 8); glava = potisni(glava, 10); console.log('Seznam pred izbrisom: '); printList(head); deleteNode(head, 7); console.log('Seznam po izbrisu: '); printList(head);> Python3 # Python program to delete a given key from linked list class Node: def __init__(self, data): self.data = data self.next = None # Function to insert a node at the # beginning of a Circular linked list def push(head, data): # Create a new node and make head as next of it. newP = Node(data) newP.next = head # If linked list is not NULL then # set the next of last node if head != None: # Find the node before head and # update next of it. temp = head while (temp.next != head): temp = temp.next temp.next = newP else: newP.next = newP head = newP return head # Function to print nodes in a given circular linked list def printList(head): if head == None: print('List is Empty') return temp = head.next print(head.data, end=' ') if (head != None): while (temp != head): print(temp.data, end=' ') temp = temp.next print() # Function to delete a given node # from the list def deleteNode(head, key): # If linked list is empty if (head == None): return # If the list contains only a # single node if (head.data == key and head.next == head): head = None return last = head # If head is to be deleted if (head.data == key): # Find the last node of the list while (last.next != head): last = last.next # Point last node to the next of # head i.e. the second node # of the list last.next = head.next head = last.next return # Either the node to be deleted is # not found or the end of list # is not reached while (last.next != head and last.next.data != key): last = last.next # If node to be deleted was found if (last.next.data == key): d = last.next last.next = d.next d = None else: print('Given node is not found in the list!!!') # Driver code # Initialize lists as empty head = None # Created linked list will be # 2->5->7->8->10 glava = potiskaj(glava, 2) glava = potiskaj(glava, 5) glava = potiskaj(glava, 7) glava = potiskaj(glava, 8) glava = potiskaj(glava, 10) print('Seznam pred izbrisom: ') printList(head) deleteNode(head, 7) print('Seznam po izbrisu: ') printList(head)> Izhod
List Before Deletion: 10 8 7 5 2 List After Deletion: 10 8 5 2>
Časovna zapletenost: O(N), Najslabši primer se zgodi, ko je element, ki ga želite izbrisati, zadnji element in se moramo premikati po celotnem seznamu.
Pomožni prostor: O(1), Kot stalen dodatni prostor se uporablja.
Prednosti krožnih povezanih seznamov:
- Vsako vozlišče je lahko izhodišče. Če začnemo s katere koli točke, lahko prečkamo celoten seznam. Samo ustaviti se moramo, ko je prvo obiskano vozlišče ponovno obiskano.
- Uporabno za izvedbo čakalne vrste. Za razliko od to implementacije nam ni treba vzdrževati dveh kazalcev za sprednji in zadnji del, če uporabljamo krožni povezani seznam. Ohranjamo lahko kazalec na zadnje vstavljeno vozlišče in sprednjo stran lahko vedno pridobimo kot zadnjo predzadnjo.
- Krožni seznami so uporabni v aplikacijah za večkratno kroženje po seznamu. Na primer, ko se na osebnem računalniku izvaja več aplikacij, je običajno, da operacijski sistem postavi izvajajoče se aplikacije na seznam in nato kroži med njimi, tako da vsaki od njih da določen čas za izvedbo, nato pa jih pusti, da počakajo, CPE je dodeljen drugi aplikaciji. Primerno je, da operacijski sistem uporablja krožni seznam, tako da se lahko, ko doseže konec seznama, pomakne na začetek seznama.
- Krožni dvojno povezani seznami se uporabljajo za implementacijo naprednih podatkovnih struktur, kot je Fibonaccijeva kopica .
- Implementacija krožnega povezanega seznama je lahko razmeroma enostavna v primerjavi z drugimi kompleksnejšimi podatkovnimi strukturami, kot so drevesa ali grafi.
Slabosti krožnega povezanega seznama:
- V primerjavi z enojno povezanimi seznami so krožni seznami bolj zapleteni.
- Obračanje krožnega seznama je bolj zapleteno kot enojno ali dvojno obračanje krožnega seznama.
- Možno je, da gre koda v neskončno zanko, če z njo ne ravnamo previdno.
- Težje je najti konec seznama in nadzorovati zanko.
- Čeprav so lahko krožni povezani seznami učinkoviti v določenih aplikacijah, je lahko njihovo delovanje v določenih primerih počasnejše od drugih podatkovnih struktur, na primer ko je treba seznam razvrstiti ali preiskati.
- Krožni povezani seznami ne zagotavljajo neposrednega dostopa do posameznih vozlišč
Uporaba krožnih povezanih seznamov:
- Igre za več igralcev uporabljajo to, da lahko vsak igralec igra.
- Krožni povezani seznam se lahko uporablja za organiziranje več delujočih aplikacij v operacijskem sistemu. Te aplikacije ponavlja operacijski sistem.
- Krožne povezane sezname je mogoče uporabiti pri težavah z dodeljevanjem virov.
- Krožni povezani seznami se običajno uporabljajo za implementacijo krožnih medpomnilnikov,
- Krožne povezane sezname je mogoče uporabiti v simulacijah in igrah.
Zakaj krožno povezan seznam?
- Vozlišče vedno kaže na drugo vozlišče, zato dodelitev NULL ni potrebna.
- Kot začetno točko lahko nastavite katero koli vozlišče.
- Vozlišča se hitro prečkajo od prvega do zadnjega.
Naslednje objave: Krožni povezani seznam | 2. sklop (prehod) Krožni enojno povezani seznam | Vstavljanje Prosimo, napišite komentarje, če najdete kakšno napako v zgornji kodi/algoritmu, ali poiščite druge načine za rešitev iste težave
