Kvadrant je definiran kot območje v prostoru, ki je razdeljeno na štiri enake dele z dvema osema, in sicer z osjo X in osjo Y v kartezični ravnini. Ti dve osi se sekata pod kotom 90 stopinj in štiri tako oblikovane regije se imenujejo štirje kvadranti, in sicer I kvadrant, II kvadrant, III kvadrant in IV kvadrant.
pretvorba niza v int v Javi
V tem članku bomo raziskali bistvene koncepte kvadranta, vključno s tem, kaj je kvadrant, njegovo ploščino, graf kvadranta, kartezično ravnino, pravila znakov znotraj kvadranta, absciso in koordinato, kot tudi izris točk na kvadrantu.
Kazalo
- Kaj so kvadranti grafa?
- Konvencija znakov v kvadrantih
- Risanje točk na kvadrantih
- Trigonometrične vrednosti v različnih kvadrantih
Kaj so kvadranti grafa?
Kvadrant je določeno območje na a kartezična ravnina , ki nastane s presečiščem osi X in Y. V tej ravnini so oblikovani štirje kvadranti, vsak s svojimi edinstvenimi lastnostmi. Prvi kvadrant v zgornjem desnem kotu ima pozitivni koordinati x in y. Drugi kvadrant v zgornjem levem kotu ima negativne x in pozitivne koordinate y itd. Razumevanje teh kvadrantov je bistvenega pomena za lociranje in razlago točk na grafu, kar zagotavlja sistematičen način za navigacijo in analizo kartezičnih koordinat.
4 kvadranti na koordinatni ravnini
Kartezična ravnina, ki jo tvorita osi X in Y, je razdeljena na štiri kvadrante, od katerih ima vsak svoje značilnosti:
- Prvi kvadrant: Koordinate x in y, ki se nahajajo zgoraj desno, so pozitivne. Ta kvadrant predstavlja točke v zgornjem desnem delu ravnine.
- Drugi kvadrant: V zgornjem levem kotu je x-koordinata negativna, y-koordinata pa pozitivna. Ta kvadrant pokriva točke v zgornjem levem delu ravnine.
- Tretji kvadrant: Koordinate x in y, postavljene spodaj levo, so negativne. Točke v spodnjem levem območju ravnine spadajo v ta kvadrant.
- Četrti kvadrant: V spodnjem desnem kotu je x-koordinata pozitivna, y-koordinata pa negativna. Ta kvadrant vključuje točke v spodnjem desnem delu ravnine.
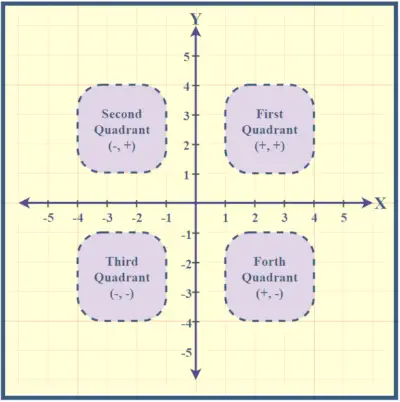
Kvadranti so oštevilčeni v nasprotni smeri urinega kazalca, začenši od zgornje desne strani. Točka, kjer se sekata osi X in Y, se imenuje izhodišče, s koordinatami (0,0), ki označujejo ničelne vrednosti za x in y. Razumevanje teh kvadrantov pomaga locirati točke znotraj kartezične ravnine.
Kaj je Origin?
Začetna točka na grafu, znana kot izhodišče in prikazana kot (0, 0), je točka, kjer se sekata vodoravna os x in navpična os y. To pomeni, da sta v izvoru vrednosti za x in y enaki nič. Služi kot referenčna točka za lociranje drugih točk na grafu. Na zgoraj dodani sliki točka O prikazuje izhodišče.
Abscisa in ordinata v kvadrantih
V štirih kvadrantih so števila predstavljena kot pari (a, b), kjer 'a' pomeni x-koordinato, 'b' pa y-koordinato. Če želite brez izrisa ugotoviti, kje je točka, bodite pozorni na predznaka koordinate x (abscisa) in koordinate y (ordinata). Na primer, če imate točko, kot je Q (3, -5), znaki (+ve, -ve) označujejo, da je v kvadrantu IV.
Abscisa prikazuje vodoravno razdaljo od osi Y. Pozitivna abscisa pomeni desno, v našem primeru pa abscisa = 3 pomeni iti desno od izhodišča vzdolž osi x za 3 enote.
Ordinata označuje navpično razdaljo od izhodišča. Negativna ordinata pomeni spuščanje od izhodišča vzdolž osi y. V primeru ordinata = -5 pomeni zmanjšanje za 5 enot.
Konvencija znakov v kvadrantih
Dogovore o znakih v kvadrantih je mogoče enostavno razumeti z uporabo spodnje slike,

V ravnini XY, ko se premikamo od leve proti desni vzdolž osi x, se koordinata x povečuje. Podobno vzdolž osi y premik od spodaj navzgor povzroči povečanje koordinate y. Ravnina XY je razdeljena na štiri kvadrante, od katerih ima vsak poseben predznak za koordinate x in y:
| Kvadrant | x-koordinata | y-koordinata |
|---|---|---|
| 1. kvadrant | pozitivno (+) | pozitivno (+) |
| 2. kvadrant | Negativno (-) | pozitivno (+) |
| 3. kvadrant | Negativno (-) | Negativno (-) |
| 4. kvadrant | pozitivno (+) | Negativno (-) |
Zato imajo točke v 1. kvadrantu pozitivne vrednosti za x in y, točke v 2. kvadrantu imajo negativen x in pozitiven y, 3. kvadrant ima obe negativni vrednosti x in y, četrti kvadrant pa ima pozitiven x in negativen y.
Risanje točk na kvadrantih
V kartezični ravnini so točke označene z osjo x in osjo y. Te točke so označene kot (a, b), kjer je 'a' x-koordinata (abscisa), 'b' pa y-koordinata (ordinata). Za postavitev točke v kvadrantu upoštevamo predznake teh koordinat. Vrednosti x in y predstavljata, kako daleč je točka od osi x oziroma y.
Na primer, narišite točko (2, -5) na kartezični ravnini. Analiza predznaka koordinat razkrije, da je točka v 4. kvadrantu. Od osi x (desno) bo oddaljen 2 enoti in od osi y (navzdol) 5 enot, pri čemer bo kot referenčna točka uporabljen izvor.
zemljevid proti nizu
Trigonometrične vrednosti v različnih kvadrantih
Vrednote različnih trigonometrične funkcije v različnih kvadrantih se lahko naučite s preučevanjem spodnje tabele kot,
| Kvadrant | brez | Cos | torej | Kosekans | Sekant | Kotangens |
|---|---|---|---|---|---|---|
| 1. kvadrant | + | + | + | + | + | + |
| 2. kvadrant | + | – | + | + | – | – |
| 3. kvadrant | – | – | – | – | – | + |
| 4. kvadrant | – | – | – | – | + | – diagram modela e-r |
V 1. kvadrantu so vsa trigonometrična razmerja pozitivna. V 2. kvadrantu sta sinus in kosekans pozitivna (+), medtem ko sta kosinus in sekans negativna (-). V 3. kvadrantu sta tangens in kotangens pozitivna (+), kosinus in sekans pa negativna (-). V 4. kvadrantu sta sinus in kosekans negativna (-), medtem ko sta kosinus in sekans pozitivna (+).
Preberi več,
- Koordinatna geometrija
- Vzporedne črte
- Formula razdalje
Rešeni primeri na kvadrantu
Primer 1: Narišite točko A (3, -4) in določite njen kvadrant.
rešitev:
Točka A se nahaja na koordinatah (3, -4). Ker je x-koordinata pozitivna (3) in y-koordinata negativna (-4), leži točka A v kvadrantu IV.
Primer 2: Narišite točko P (-5, 2) in določite njen kvadrant
rešitev:
Koordinate točke P so (-5, 2). Za določitev kvadranta preučimo predznake koordinat x in y.
X-koordinata je -5, kar označuje položaj levo od izhodišča.
Y-koordinata je 2 in označuje položaj nad izhodiščem.
Ker je torej x-koordinata negativna in y-koordinata pozitivna, se točka P nahaja v kvadrantu II.
Točka P (-5, 2) se nahaja v kvadrantu II kartezične ravnine.
Vadbene naloge na kvadrantih
Problem 1: Narišite točko (1, -1) in določite njen kvadrant.
Problem 2: Poiščite tri točke na osi x in določite njihove kvadrante.
Problem 3: Če točka leži na osi y s koordinatami (0, -3), v katerem kvadrantu je?
Problem 4: Poiščite točke Q (2, 2), R (-2, -2) in S (0, 0) in preverite kolinearnost.
Problem 5: Narišite točko (-4, -3) in razložite, v katerem kvadrantu se nahaja.
Pogosta vprašanja o kvadrantih
1. Kaj je kvadrant v matematiki?
V matematiki je kvadrant eden od štirih odsekov, ki nastanejo s presečiščem dveh pravokotnih črt ali osi. Te osi so običajno označene kot os x in os y v kartezičnem koordinatnem sistemu.
2. Kako se imenuje presečišče dveh osi?
Sečišče dveh osi v kartezičnem koordinatnem sistemu imenujemo izhodišče. Predstavljena je s točko, kjer se stikata osi x in osi y, običajno označeno kot (0,0).
3. Kaj so 4 kvadranti?
Štirje kvadranti so odseki, ki nastanejo z razdelitvijo kartezične koordinatne ravnine na štiri enake dele. Označeni so kot prvi kvadrant (Q1), drugi kvadrant (Q2), tretji kvadrant (Q3) in četrti kvadrant (Q4).
4. Kateri kvadrant je pozitiven?
Pozitivni kvadrant v kartezičnem koordinatnem sistemu je prvi kvadrant (Q1). V tem kvadrantu sta koordinati x in y pozitivni.
5. Kakšna je uporaba kvadrantov v grafih?
Kvadranti v grafih zagotavljajo sistematičen način organiziranja in lociranja točk na podlagi njihovih koordinat. Pomagajo pri vizualizaciji odnosov med spremenljivkami in analizi vzorcev v nizih podatkov, kar olajša interpretacijo grafičnih predstavitev.
6. Kateri kvadrant ima obe vrednosti koordinat pozitivne?
Prvi kvadrant (Q1) je kvadrant, kjer sta koordinati točk x in y pozitivni. Je edini kvadrant z obema pozitivnima vrednostma.
7. Kaj so 4 kvadranti kroga?
Koncept kvadrantov ni neposredno uporaben za kroge. Namesto tega so krogi razdeljeni na kote, merjene v stopinjah. Če pa govorimo o krožnih sektorjih, lahko uporabimo izraze, kot so prvi sektor, drugi sektor, tretji sektor in četrti sektor, ki ustrezajo različnim kotnim regijam.
