The Floyd-Warshallov algoritem , poimenovan po svojih ustvarjalcih Robert Floyd in Stephen Warshall , je temeljni algoritem v računalništvu in teoriji grafov. Uporablja se za iskanje najkrajših poti med vsemi pari vozlišč v uteženem grafu. Ta algoritem je zelo učinkovit in lahko obravnava grafe z obema pozitivno in n negativne uteži robov , zaradi česar je vsestransko orodje za reševanje številnih težav z omrežjem in povezljivostjo.
Kazalo
- Floyd Warshallov algoritem
- Ideja za Floyd Warshallov algoritem
- Algoritem Floyd Warshall Algoritem
- Psevdo koda algoritma Floyda Warshalla
- Ilustracija algoritma Floyda Warshalla
- Analiza kompleksnosti algoritma Floyda Warshalla
- Zakaj je Floyd-Warshallov algoritem boljši za goste grafe in ne za redke grafe?
- Pomembna vprašanja za intervju, povezana s Floyd-Warshall
- Uporaba algoritma Floyd-Warshall v resničnem svetu
Algoritem Floyda Warshalla:
The Floyd Warshallov algoritem je algoritem vseh parov najkrajše poti za razliko od Dijkstra in Bellman Ford ki so algoritmi najkrajše poti z enim virom. Ta algoritem deluje tako za usmeril in neusmerjeno uteženo grafi. Vendar ne deluje za grafe z negativnimi cikli (kjer je vsota robov v ciklu negativna). Sledi Dinamično programiranje pristop za preverjanje vsake možne poti, ki poteka skozi vsako možno vozlišče, da se izračuna najkrajša razdalja med vsakim parom vozlišč.
primer odprtokodnega operacijskega sistema je
Ideja za Floyd Warshallov algoritem:
Recimo, da imamo graf G[][] z IN oglišča iz 1 do n . Zdaj moramo oceniti a Matrika najkrajše poti[][] kjer s hortestPathMatrix[i][j] predstavlja najkrajšo pot med vozlišči jaz in j .
Očitno najkrajša pot med jaz do j bo imel nekaj k število vmesnih vozlišč. Ideja algoritma floyd warshall je obravnavati vsako točko iz 1 do n kot vmesno vozlišče enega za drugim.
Naslednja slika prikazuje zgornjo lastnost optimalne podstrukture v algoritmu Floyd Warshall:
Floyd Warshall Algoritem Algoritem:
- Kot prvi korak inicializirajte matriko rešitve enako kot matriko vhodnega grafa.
- Nato posodobite matriko rešitve tako, da vse točke upoštevate kot vmesno točko.
- Ideja je izbrati vsa vozlišča eno za drugim in posodobiti vse najkrajše poti, ki vključujejo izbrano točko kot vmesno točko na najkrajši poti.
- Ko izberemo številko vozlišča k kot vmesno oglišče smo že obravnavali oglišča {0, 1, 2, .. k-1} kot vmesna vozlišča.
- Za vsak par (i, j) izvornih oziroma ciljnih vozlišč sta možna dva primera.
- k ni vmesna točka na najkrajši poti od jaz do j . Ohranjamo vrednost dist[i][j] kot je.
- k je vmesna točka na najkrajši poti od jaz do j . Posodabljamo vrednost dist[i][j] kot dist[i][k] + dist[k][j], če dist[i][j]> dist[i][k] + dist[k][j]
Psevdo-koda algoritma Floyda Warshalla:>
Za k = 0 do n – 1
Za i = 0 do n – 1
Za j = 0 do n – 1
Razdalja [i, j] = min (razdalja [i, j], razdalja [i, k] + razdalja [k, j])kjer je i = izvorno vozlišče, j = ciljno vozlišče, k = vmesno vozlišče
Ilustracija algoritma Floyda Warshalla:
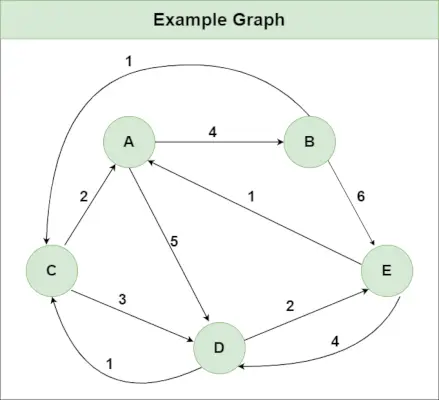
Priporočena praksa Poskusite!Recimo, da imamo graf, kot je prikazan na sliki:
10 ml v ozKorak 1 : Inicializirajte matriko razdalje[][] z uporabo vhodnega grafa, tako da je razdalja[i][j]= teža roba od jaz do j , tudi Razdalja[i][j] = Neskončnost, če ni roba od jaz do j.
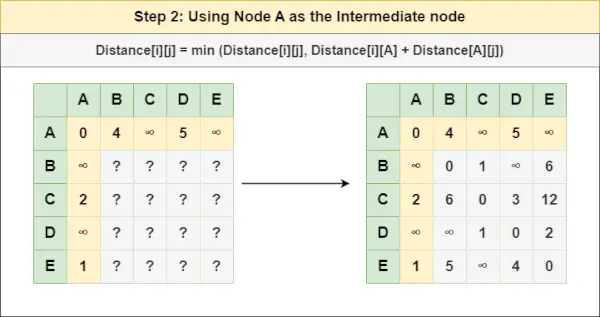
2. korak : Zdravite vozlišče A kot vmesno vozlišče in izračunajte razdaljo [][] za vsak par vozlišč {i,j} z uporabo formule:
= Razdalja[i][j] = najmanjša (Razdalja[i][j], (Razdalja od i do A ) + (Oddaljenost od A za j ))
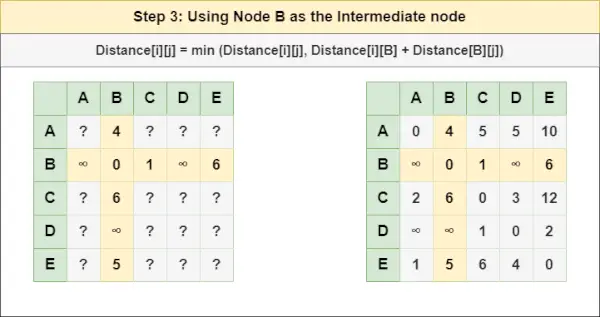
= Razdalja[i][j] = najmanj (Razdalja[i][j], Razdalja[i][ A ] + Razdalja[ A ][j])3. korak : Zdravite vozlišče B kot vmesno vozlišče in izračunajte razdaljo [][] za vsak par vozlišč {i,j} z uporabo formule:
= Razdalja[i][j] = najmanjša (Razdalja[i][j], (Razdalja od i do B ) + (Oddaljenost od B za j ))
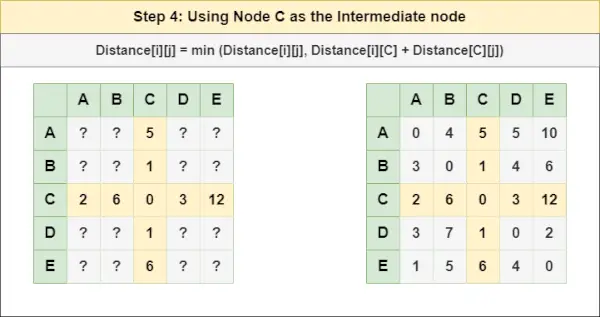
= Razdalja[i][j] = najmanj (Razdalja[i][j], Razdalja[i][ B ] + Razdalja[ B ][j])4. korak : Zdravite vozlišče C kot vmesno vozlišče in izračunajte razdaljo [][] za vsak par vozlišč {i,j} z uporabo formule:
= Razdalja[i][j] = najmanjša (Razdalja[i][j], (Razdalja od i do C ) + (Oddaljenost od C za j ))
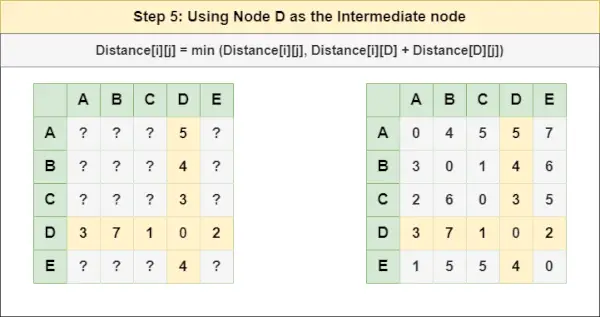
= Razdalja[i][j] = najmanj (Razdalja[i][j], Razdalja[i][ C ] + Razdalja[ C ][j])5. korak : Zdravite vozlišče D kot vmesno vozlišče in izračunajte razdaljo [][] za vsak par vozlišč {i,j} z uporabo formule:
blokiranih stikov= Razdalja[i][j] = najmanjša (Razdalja[i][j], (Razdalja od i do D ) + (Oddaljenost od D za j ))
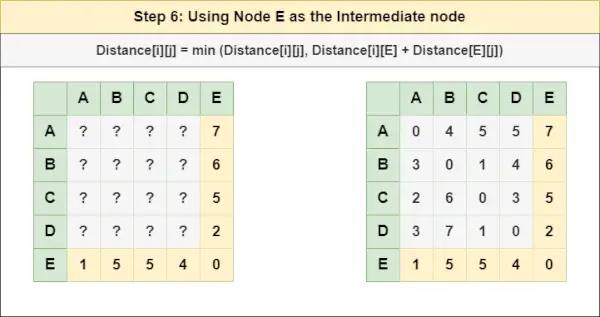
= Razdalja[i][j] = najmanj (Razdalja[i][j], Razdalja[i][ D ] + Razdalja[ D ][j])6. korak : Zdravite vozlišče IN kot vmesno vozlišče in izračunajte razdaljo [][] za vsak par vozlišč {i,j} z uporabo formule:
= Razdalja[i][j] = najmanjša (Razdalja[i][j], (Razdalja od i do IN ) + (Oddaljenost od IN za j ))
= Razdalja[i][j] = najmanj (Razdalja[i][j], Razdalja[i][ IN ] + Razdalja[ IN ][j])korak 7 : Ker so bila vsa vozlišča obravnavana kot vmesna vozlišča, lahko zdaj vrnemo posodobljeno matriko razdalje [][] kot našo matriko odgovorov.
Spodaj je izvedba zgornjega pristopa:
C++ // C++ Program for Floyd Warshall Algorithm #include using namespace std; // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough value.This value will be used for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) { int i, j, k; /* Add all vertices one by one to the set of intermediate vertices. --->Pred začetkom iteracije imamo najkrajše razdalje med vsemi pari tock, tako da najkrajše razdalje upoštevajo samo tocke v nizu {0, 1, 2, .. k-1} kot vmesne tocke. ----> Po koncu iteracije se vozlišče št. k je dodan nizu vmesnih vozlišč in niz postane {0, 1, 2, .. k} */ za (k = 0; k< V; k++) { // Pick all vertices as source one by one for (i = 0; i < V; i++) { // Pick all vertices as destination for the // above picked source for (j = 0; j < V; j++) { // If vertex k is on the shortest path from // i to j, then update the value of // dist[i][j] if (dist[i][j]>(dist[i][k] + dist[k][j]) && (dist[k][j] != INF && dist[i][k] != INF)) dist[i][j] = dist[i][k] + dist[k][j]; } } } // Izpis matrike najkrajše razdalje printSolution(dist); } /* Pomožna funkcija za tiskanje rešitve */ void printSolution(int dist[][V]) { cout<< 'The following matrix shows the shortest ' 'distances' ' between every pair of vertices
'; for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) { if (dist[i][j] == INF) cout << 'INF' << ' '; else cout << dist[i][j] << ' '; } cout << endl; } } // Driver's code int main() { /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int graph[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } }; // Klic funkcije floydWarshall(graph); vrni 0; } // To kodo je prispeval Mythri J L> C // C Program for Floyd Warshall Algorithm #include // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough value. This value will be used for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) { int i, j, k; /* Add all vertices one by one to the set of intermediate vertices. --->Pred začetkom iteracije imamo najkrajše razdalje med vsemi pari tock, tako da najkrajše razdalje upoštevajo samo tocke v nizu {0, 1, 2, .. k-1} kot vmesne tocke. ----> Po koncu iteracije se vozlišče št. k je dodan nizu vmesnih vozlišč in niz postane {0, 1, 2, .. k} */ za (k = 0; k< V; k++) { // Pick all vertices as source one by one for (i = 0; i < V; i++) { // Pick all vertices as destination for the // above picked source for (j = 0; j < V; j++) { // If vertex k is on the shortest path from // i to j, then update the value of // dist[i][j] if (dist[i][k] + dist[k][j] < dist[i][j]) dist[i][j] = dist[i][k] + dist[k][j]; } } } // Print the shortest distance matrix printSolution(dist); } /* A utility function to print solution */ void printSolution(int dist[][V]) { printf( 'The following matrix shows the shortest distances' ' between every pair of vertices
'); for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) { if (dist[i][j] == INF) printf('%7s', 'INF'); else printf('%7d', dist[i][j]); } printf('
'); } } // driver's code int main() { /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int graph[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } }; // Klic funkcije floydWarshall(graph); vrni 0; }> Java // Java program for Floyd Warshall All Pairs Shortest // Path algorithm. import java.io.*; import java.lang.*; import java.util.*; class AllPairShortestPath { final static int INF = 99999, V = 4; void floydWarshall(int dist[][]) { int i, j, k; /* Add all vertices one by one to the set of intermediate vertices. --->Pred začetkom iteracije imamo najkrajše razdalje med vsemi pari tock, tako da najkrajše razdalje upoštevajo samo tocke v nizu {0, 1, 2, .. k-1} kot vmesne tocke. ----> Po koncu iteracije se vozlišče št. k je dodan nizu vmesnih vozlišč in niz postane {0, 1, 2, .. k} */ za (k = 0; k< V; k++) { // Pick all vertices as source one by one for (i = 0; i < V; i++) { // Pick all vertices as destination for the // above picked source for (j = 0; j < V; j++) { // If vertex k is on the shortest path // from i to j, then update the value of // dist[i][j] if (dist[i][k] + dist[k][j] < dist[i][j]) dist[i][j] = dist[i][k] + dist[k][j]; } } } // Print the shortest distance matrix printSolution(dist); } void printSolution(int dist[][]) { System.out.println( 'The following matrix shows the shortest ' + 'distances between every pair of vertices'); for (int i = 0; i < V; ++i) { for (int j = 0; j < V; ++j) { if (dist[i][j] == INF) System.out.print('INF '); else System.out.print(dist[i][j] + ' '); } System.out.println(); } } // Driver's code public static void main(String[] args) { /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int graph[][] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1}, {INF, INF, INF, 0}}; AllPairShortestPath a = new AllPairShortestPath(); // Klic funkcije a.floydWarshall(graph); } } // Prispeval Aakash Hasija> Python3 # Python3 Program for Floyd Warshall Algorithm # Number of vertices in the graph V = 4 # Define infinity as the large # enough value. This value will be # used for vertices not connected to each other INF = 99999 # Solves all pair shortest path # via Floyd Warshall Algorithm def floydWarshall(graph): ''' dist[][] will be the output matrix that will finally have the shortest distances between every pair of vertices ''' ''' initializing the solution matrix same as input graph matrix OR we can say that the initial values of shortest distances are based on shortest paths considering no intermediate vertices ''' dist = list(map(lambda i: list(map(lambda j: j, i)), graph)) ''' Add all vertices one by one to the set of intermediate vertices. --->Pred začetkom iteracije imamo najkrajše razdalje med vsemi pari tock, tako da najkrajše razdalje upoštevajo samo tocke v nizu {0, 1, 2, .. k-1} kot vmesne tocke. ----> Po koncu iteracije se vozlišče št. k je dodan naboru vmesnih tock in nabor postane {0, 1, 2, .. k} ''' za k v obsegu (V): # izberi vse tocke kot vir eno za drugo za i v range(V): # Izberi vse točke kot cilj za # zgoraj izbran vir za j v range(V): # Če je točka k na najkrajši poti od # i do j, potem posodobi vrednost dist[i][ j] dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j] ) printSolution(dist) # Pomožna funkcija za tiskanje rešitve def printSolution (dist): print('Naslednja matrika prikazuje najkrajše razdalje med vsakim parom vozlišč') za i v obsegu(V): za j v obsegu(V): if(dist[i][j] == INF): print('%7s' % ('INF'), end=' ') else: print('%7d ' % (dist[i][j]), end=' ') if j == V-1: print() # Koda gonilnika if __name__ == '__main__': ''' 10 (0)------ ->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 ''' graf = [[0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0 , 1], [INF, INF, INF, 0] ] # Klic funkcije floydWarshall(graph) # To kodo je prispeval Mythri J L> C# // C# program for Floyd Warshall All // Pairs Shortest Path algorithm. using System; public class AllPairShortestPath { readonly static int INF = 99999, V = 4; void floydWarshall(int[, ] graph) { int[, ] dist = new int[V, V]; int i, j, k; // Initialize the solution matrix // same as input graph matrix // Or we can say the initial // values of shortest distances // are based on shortest paths // considering no intermediate // vertex for (i = 0; i < V; i++) { for (j = 0; j < V; j++) { dist[i, j] = graph[i, j]; } } /* Add all vertices one by one to the set of intermediate vertices. --->Pred začetkom iteracije imamo najkrajše razdalje med vsemi pari tock, tako da najkrajše razdalje upoštevajo samo tocke v nizu {0, 1, 2, .. k-1} kot vmesne tocke. ---> Po koncu iteracije se vozlišče št. k je dodan nizu vmesnih vozlišč in niz postane {0, 1, 2, .. k} */ za (k = 0; k< V; k++) { // Pick all vertices as source // one by one for (i = 0; i < V; i++) { // Pick all vertices as destination // for the above picked source for (j = 0; j < V; j++) { // If vertex k is on the shortest // path from i to j, then update // the value of dist[i][j] if (dist[i, k] + dist[k, j] < dist[i, j]) { dist[i, j] = dist[i, k] + dist[k, j]; } } } } // Print the shortest distance matrix printSolution(dist); } void printSolution(int[, ] dist) { Console.WriteLine( 'Following matrix shows the shortest ' + 'distances between every pair of vertices'); for (int i = 0; i < V; ++i) { for (int j = 0; j < V; ++j) { if (dist[i, j] == INF) { Console.Write('INF '); } else { Console.Write(dist[i, j] + ' '); } } Console.WriteLine(); } } // Driver's Code public static void Main(string[] args) { /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int[, ] graph = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0 , 1 }, { INF, INF, INF, 0 } }; AllPairShortestPath a = new AllPairShortestPath(); // Klic funkcije a.floydWarshall(graph); } } // Ta članek je prispeval // Abdul Mateen Mohammed> Javascript // A JavaScript program for Floyd Warshall All // Pairs Shortest Path algorithm. var INF = 99999; class AllPairShortestPath { constructor() { this.V = 4; } floydWarshall(graph) { var dist = Array.from(Array(this.V), () =>nov Array(this.V).fill(0)); var i, j, k; // Inicializiraj matriko rešitve // enako kot matriko vhodnega grafa // Lahko pa rečemo, da začetne // vrednosti najkrajših razdalj // temeljijo na najkrajših poteh // brez upoštevanja vmesne // točke za (i = 0; i< this.V; i++) { for (j = 0; j < this.V; j++) { dist[i][j] = graph[i][j]; } } /* Add all vertices one by one to the set of intermediate vertices. --->Pred začetkom iteracije imamo najkrajše razdalje med vsemi pari tock, tako da najkrajše razdalje upoštevajo samo tocke v nizu {0, 1, 2, .. k-1} kot vmesne tocke. ---> Po koncu iteracije se vozlišče št. k se doda nizu vmesnih vozlišč in niz postane {0, 1, 2, .. k} */ za (k = 0; k< this.V; k++) { // Pick all vertices as source // one by one for (i = 0; i < this.V; i++) { // Pick all vertices as destination // for the above picked source for (j = 0; j < this.V; j++) { // If vertex k is on the shortest // path from i to j, then update // the value of dist[i][j] if (dist[i][k] + dist[k][j] < dist[i][j]) { dist[i][j] = dist[i][k] + dist[k][j]; } } } } // Print the shortest distance matrix this.printSolution(dist); } printSolution(dist) { document.write( 'Following matrix shows the shortest ' + 'distances between every pair of vertices ' ); for (var i = 0; i < this.V; ++i) { for (var j = 0; j < this.V; ++j) { if (dist[i][j] == INF) { document.write(' INF '); } else { document.write(' ' + dist[i][j] + ' '); } } document.write(' '); } } } // Driver Code /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ var graph = [ [0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0, 1] , [INF, INF, INF, 0], ]; var a = new AllPairShortestPath(); // Izpis rešitve a.floydWarshall(graph); // To kodo je prispeval rdtaank.> PHP // PHP Program for Floyd Warshall Algorithm // Solves the all-pairs shortest path problem // using Floyd Warshall algorithm function floydWarshall ($graph, $V, $INF) { /* dist[][] will be the output matrix that will finally have the shortest distances between every pair of vertices */ $dist = array(array(0,0,0,0), array(0,0,0,0), array(0,0,0,0), array(0,0,0,0)); /* Initialize the solution matrix same as input graph matrix. Or we can say the initial values of shortest distances are based on shortest paths considering no intermediate vertex. */ for ($i = 0; $i < $V; $i++) for ($j = 0; $j < $V; $j++) $dist[$i][$j] = $graph[$i][$j]; /* Add all vertices one by one to the set of intermediate vertices. --->Pred začetkom iteracije imamo najkrajše razdalje med vsemi pari tock, tako da najkrajše razdalje upoštevajo samo tocke v nizu {0, 1, 2, .. k-1} kot vmesne tocke. ----> Po koncu iteracije se vozlišče št. k se doda nizu vmesnih vozlišč in niz postane {0, 1, 2, .. k} */ za ($k = 0; $k< $V; $k++) { // Pick all vertices as source one by one for ($i = 0; $i < $V; $i++) { // Pick all vertices as destination // for the above picked source for ($j = 0; $j < $V; $j++) { // If vertex k is on the shortest path from // i to j, then update the value of dist[i][j] if ($dist[$i][$k] + $dist[$k][$j] < $dist[$i][$j]) $dist[$i][$j] = $dist[$i][$k] + $dist[$k][$j]; } } } // Print the shortest distance matrix printSolution($dist, $V, $INF); } /* A utility function to print solution */ function printSolution($dist, $V, $INF) { echo 'The following matrix shows the ' . 'shortest distances between ' . 'every pair of vertices
'; for ($i = 0; $i < $V; $i++) { for ($j = 0; $j < $V; $j++) { if ($dist[$i][$j] == $INF) echo 'INF ' ; else echo $dist[$i][$j], ' '; } echo '
'; } } // Drivers' Code // Number of vertices in the graph $V = 4 ; /* Define Infinite as a large enough value. This value will be used for vertices not connected to each other */ $INF = 99999 ; /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ $graf = matrika(matrika(0, 5, $INF, 10), matrika($INF, 0, 3, $INF), matrika($ INF, $INF, 0, 1), niz ($INF, $INF, $INF, 0)); // Klic funkcije floydWarshall($graph, $V, $INF); // To kodo je prispeval Ryuga ?>> Izhod
The following matrix shows the shortest distances between every pair of vertices 0 5 8 9 INF 0 3 4 INF INF 0 1 INF INF INF 0>
Analiza kompleksnosti algoritma Floyd Warshall:
- Časovna zapletenost: O(V3), kjer je V število vozlišč v grafu in izvajamo tri ugnezdene zanke velikosti V
- Pomožni prostor: O(V2), da ustvarite 2-D matriko za shranjevanje najkrajše razdalje za vsak par vozlišč.
Opomba : Zgornji program natisne samo najkrajše razdalje. Rešitev lahko spremenimo za tiskanje najkrajših poti tudi s shranjevanjem informacij o predhodniku v ločeni 2D matriki.
čas večerje proti večerji
Zakaj je Floyd-Warshallov algoritem boljši za goste grafe in ne za redke grafe?
Gost graf : Graf, v katerem je število robov znatno veliko večje od števila vozlišč.
Redki graf : Graf, v katerem je število robov zelo nizko.Ne glede na to, koliko robov je v grafu Floyd Warshallov algoritem teče za O(V3) krat, zato je najprimernejši za Gosti grafi . V primeru redkih grafov, Johnsonov algoritem je bolj primeren.
Pomembna vprašanja za intervju v zvezi s Floyd-Warshall:
- Kako zaznati negativni cikel v grafu z algoritmom Floyd Warshall?
- V čem se Floyd-Warshallov algoritem razlikuje od Dijkstrinega algoritma?
- Kako se algoritem Floyd-Warshall razlikuje od algoritma Bellman-Ford?
Uporaba algoritma Floyd-Warshall v resničnem svetu:
- V računalniškem omrežju lahko algoritem uporabimo za iskanje najkrajše poti med vsemi pari vozlišč v omrežju. To se imenuje kot omrežno usmerjanje .
- Povezljivost letov V letalski industriji iskanje najkrajše poti med letališči.
- GIS ( Geografski informacijski sistemi ) aplikacije pogosto vključujejo analizo prostorskih podatkov, kot so cestna omrežja, za iskanje najkrajših poti med lokacijami.
- Kleenejev algoritem ki je posplošitev besede floyd warshall, se lahko uporabi za iskanje regularnega izraza za običajni jezik.