Evklidski algoritem je način za iskanje največjega skupnega delitelja dveh pozitivnih celih števil. GCD dveh števil je največje število, ki obe deli. Preprost način za iskanje GCD je faktorizacija obeh števil in množenje skupnih prafaktorjev.
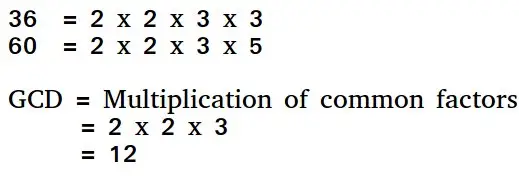
Osnovni evklidski algoritem za GCD:
Algoritem temelji na spodnjih dejstvih.
- Če od večjega odštejemo manjše število (zmanjšamo večje število), se GCD ne spremeni. Torej, če vedno znova odštevamo večje od dveh, dobimo GCD.
- Zdaj namesto odštevanja, če delimo manjše število, se algoritem ustavi, ko najdemo ostanek 0.
Spodaj je rekurzivna funkcija za vrednotenje gcd z uporabo Evklidovega algoritma:
C
// C program to demonstrate Basic Euclidean Algorithm> #include> // Function to return gcd of a and b> int> gcd(>int> a,>int> b)> {> >if> (a == 0)> >return> b;> >return> gcd(b % a, a);> }> // Driver code> int> main()> {> >int> a = 10, b = 15;> > >// Function call> >printf>(>'GCD(%d, %d) = %d
'>, a, b, gcd(a, b));> >a = 35, b = 10;> >printf>(>'GCD(%d, %d) = %d
'>, a, b, gcd(a, b));> >a = 31, b = 2;> >printf>(>'GCD(%d, %d) = %d
'>, a, b, gcd(a, b));> >return> 0;> }> |
>
>
CPP
// C++ program to demonstrate> // Basic Euclidean Algorithm> #include> using> namespace> std;> // Function to return> // gcd of a and b> int> gcd(>int> a,>int> b)> {> >if> (a == 0)> >return> b;> >return> gcd(b % a, a);> }> // Driver Code> int> main()> {> >int> a = 10, b = 15;> > >// Function call> >cout <<>'GCD('> << a <<>', '> << b <<>') = '> << gcd(a, b)> ><< endl;> >a = 35, b = 10;> >cout <<>'GCD('> << a <<>', '> << b <<>') = '> << gcd(a, b)> ><< endl;> >a = 31, b = 2;> >cout <<>'GCD('> << a <<>', '> << b <<>') = '> << gcd(a, b)> ><< endl;> >return> 0;> }> |
>
oblikovalnik nizov
>
Java
// Java program to demonstrate Basic Euclidean Algorithm> import> java.lang.*;> import> java.util.*;> class> GFG {> >// extended Euclidean Algorithm> >public> static> int> gcd(>int> a,>int> b)> >{> >if> (a ==>0>)> >return> b;> >return> gcd(b % a, a);> >}> >// Driver code> >public> static> void> main(String[] args)> >{> >int> a =>10>, b =>15>, g;> > >// Function call> >g = gcd(a, b);> >System.out.println(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a =>35>;> >b =>10>;> >g = gcd(a, b);> >System.out.println(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a =>31>;> >b =>2>;> >g = gcd(a, b);> >System.out.println(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >}> }> // Code Contributed by Mohit Gupta_OMG> |
>
>
Python3
# Python3 program to demonstrate Basic Euclidean Algorithm> # Function to return gcd of a and b> def> gcd(a, b):> >if> a>=>=> 0>:> >return> b> >return> gcd(b>%> a, a)> # Driver code> if> __name__>=>=> '__main__'>:> >a>=> 10> >b>=> 15> >print>(>'gcd('>, a,>','>, b,>') = '>, gcd(a, b))> >a>=> 35> >b>=> 10> >print>(>'gcd('>, a,>','>, b,>') = '>, gcd(a, b))> >a>=> 31> >b>=> 2> >print>(>'gcd('>, a,>','>, b,>') = '>, gcd(a, b))> # Code Contributed By Mohit Gupta_OMG> |
>
>
C#
// C# program to demonstrate Basic Euclidean Algorithm> using> System;> class> GFG {> >public> static> int> gcd(>int> a,>int> b)> >{> >if> (a == 0)> >return> b;> >return> gcd(b % a, a);> >}> >// Driver Code> >static> public> void> Main()> >{> >int> a = 10, b = 15, g;> >g = gcd(a, b);> >Console.WriteLine(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a = 35;> >b = 10;> >g = gcd(a, b);> >Console.WriteLine(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >a = 31;> >b = 2;> >g = gcd(a, b);> >Console.WriteLine(>'GCD('> + a +>' , '> + b> >+>') = '> + g);> >}> }> // This code is contributed by ajit> |
>
>
PHP
// php program to demonstrate Basic Euclidean Algorithm> // PHP program to demonstrate // Basic Euclidean Algorithm // Function to return // gcd of a and b function gcd($a, $b) { if ($a == 0) return $b; return gcd($b % $a, $a); } // Driver Code $a = 10; $b = 15; // Function call echo 'GCD(',$a,',' , $b,') = ', gcd($a, $b); echo '
'; $a = 35; $b = 10; echo 'GCD(',$a ,',',$b,') = ', gcd($a, $b); echo '
'; $a = 31; $b = 2; echo 'GCD(',$a ,',', $b,') = ', gcd($a, $b); // This code is contributed by m_kit ?>> |
>
>
Javascript
// JavaScript program to demonstrate> // Basic Euclidean Algorithm> // Function to return> // gcd of a and b> function> gcd( a, b)> {> >if> (a == 0)> >return> b;> >return> gcd(b % a, a);> }> // Driver Code> >let a = 10, b = 15;> >document.write(>'GCD('> + a +>', '> >+ b +>') = '> + gcd(a, b) +>' '>);> > >a = 35, b = 10;> >document.write(>'GCD('> + a +>', '> >+ b +>') = '> + gcd(a, b) +>' '>);> > >a = 31, b = 2;> >document.write(>'GCD('> + a +>', '> >+ b +>') = '> + gcd(a, b) +>' '>);> // This code contributed by aashish1995> |
>
>Izhod
GCD(10, 15) = 5 GCD(35, 10) = 5 GCD(31, 2) = 1>
Časovna zapletenost: O(Log min(a, b))
Pomožni prostor: O(Dnevnik (min(a,b))
Razširjeni evklidski algoritem:
Razširjeni evklidski algoritem najde tudi cela koeficienta x in y, tako da: ax + by = gcd(a, b)
Primeri:
Vnos: a = 30, b = 20
Izhod: gcd = 10, x = 1, y = -1
(Upoštevajte, da je 30*1 + 20*(-1) = 10)Vnos: a = 35, b = 15
Izhod: gcd = 5, x = 1, y = -2
(Upoštevajte, da je 35*1 + 15*(-2) = 5)
Razširjeni evklidski algoritem posodobi rezultate gcd(a, b) z uporabo rezultatov, izračunanih z rekurzivnim klicem gcd(b%a, a). Naj sta vrednosti x in y, izračunani z rekurzivnim klicem, x1in y1. x in y se posodobita z uporabo spodnjih izrazov.
Priporočena praksa Razširjeni evklidski algoritem Poskusite!ax + by = gcd(a, b)
gcd(a, b) = gcd(b%a, a)
gcd(b%a, a) = (b%a)x1+ je1
ax + by = (b%a)x1+ je1
ax + by = (b – [b/a] * a)x1+ je1
ax + by = a(y1– [b/a] * x1) + bx1Če primerjamo LHS in RHS,
x = y1– ?b/a? * x1
y = x1
Spodaj je izvedba zgornjega pristopa:
C++
// C++ program to demonstrate working of> // extended Euclidean Algorithm> #include> using> namespace> std;> // Function for extended Euclidean Algorithm> int> gcdExtended(>int> a,>int> b,>int> *x,>int> *y)> {> >// Base Case> >if> (a == 0)> >{> >*x = 0;> >*y = 1;> >return> b;> >}> >int> x1, y1;>// To store results of recursive call> >int> gcd = gcdExtended(b%a, a, &x1, &y1);> >// Update x and y using results of> >// recursive call> >*x = y1 - (b/a) * x1;> >*y = x1;> >return> gcd;> }> // Driver Code> int> main()> {> >int> x, y, a = 35, b = 15;> >int> g = gcdExtended(a, b, &x, &y);> >cout <<>'GCD('> << a <<>', '> << b> ><<>') = '> << g << endl;> >return> 0;> }> |
>
knn
>
C
// C program to demonstrate working of extended> // Euclidean Algorithm> #include> // C function for extended Euclidean Algorithm> int> gcdExtended(>int> a,>int> b,>int> *x,>int> *y)> {> >// Base Case> >if> (a == 0)> >{> >*x = 0;> >*y = 1;> >return> b;> >}> >int> x1, y1;>// To store results of recursive call> >int> gcd = gcdExtended(b%a, a, &x1, &y1);> >// Update x and y using results of recursive> >// call> >*x = y1 - (b/a) * x1;> >*y = x1;> >return> gcd;> }> // Driver Program> int> main()> {> >int> x, y;> >int> a = 35, b = 15;> >int> g = gcdExtended(a, b, &x, &y);> >printf>(>'gcd(%d, %d) = %d'>, a, b, g);> >return> 0;> }> |
>
>
Java
// Java program to demonstrate working of extended> // Euclidean Algorithm> import> java.lang.*;> import> java.util.*;> class> GFG {> >// extended Euclidean Algorithm> >public> static> int> gcdExtended(>int> a,>int> b,>int> x,> >int> y)> >{> >// Base Case> >if> (a ==>0>) {> >x =>0>;> >y =>1>;> >return> b;> >}> >int> x1 =>1>,> >y1 =>1>;>// To store results of recursive call> >int> gcd = gcdExtended(b % a, a, x1, y1);> >// Update x and y using results of recursive> >// call> >x = y1 - (b / a) * x1;> >y = x1;> >return> gcd;> >}> >// Driver Program> >public> static> void> main(String[] args)> >{> >int> x =>1>, y =>1>;> >int> a =>35>, b =>15>;> >int> g = gcdExtended(a, b, x, y);> >System.out.print(>'gcd('> + a +>' , '> + b> >+>') = '> + g);> >}> }> |
>
>
Python3
# Python program to demonstrate working of extended> # Euclidean Algorithm> # function for extended Euclidean Algorithm> def> gcdExtended(a, b):> ># Base Case> >if> a>=>=> 0>:> >return> b,>0>,>1> >gcd, x1, y1>=> gcdExtended(b>%> a, a)> ># Update x and y using results of recursive> ># call> >x>=> y1>-> (b>/>/>a)>*> x1> >y>=> x1> >return> gcd, x, y> # Driver code> a, b>=> 35>,>15> g, x, y>=> gcdExtended(a, b)> print>(>'gcd('>, a,>','>, b,>') = '>, g)> |
imena mest v ZDA
>
>
C#
// C# program to demonstrate working> // of extended Euclidean Algorithm> using> System;> class> GFG> {> > >// extended Euclidean Algorithm> >public> static> int> gcdExtended(>int> a,>int> b,> >int> x,>int> y)> >{> >// Base Case> >if> (a == 0)> >{> >x = 0;> >y = 1;> >return> b;> >}> >// To store results of> >// recursive call> >int> x1 = 1, y1 = 1;> >int> gcd = gcdExtended(b % a, a, x1, y1);> >// Update x and y using> >// results of recursive call> >x = y1 - (b / a) * x1;> >y = x1;> >return> gcd;> >}> > >// Driver Code> >static> public> void> Main ()> >{> >int> x = 1, y = 1;> >int> a = 35, b = 15;> >int> g = gcdExtended(a, b, x, y);> >Console.WriteLine(>'gcd('> + a +>' , '> +> >b +>') = '> + g);> >}> }> |
>
>
PHP
// PHP program to demonstrate // working of extended // Euclidean Algorithm // PHP function for // extended Euclidean // Algorithm function gcdExtended($a, $b, $x, $y) { // Base Case if ($a == 0) { $x = 0; $y = 1; return $b; } // To store results // of recursive call $gcd = gcdExtended($b % $a, $a, $x, $y); // Update x and y using // results of recursive // call $x = $y - floor($b / $a) * $x; $y = $x; return $gcd; } // Driver Code $x = 0; $y = 0; $a = 35; $b = 15; $g = gcdExtended($a, $b, $x, $y); echo 'gcd(',$a; echo ', ' , $b, ')'; echo ' = ' , $g; ?>> |
>
>
Javascript
> // Javascript program to demonstrate> // working of extended> // Euclidean Algorithm> // Javascript function for> // extended Euclidean> // Algorithm> function> gcdExtended(a, b,> >x, y)> {> >// Base Case> >if> (a == 0)> >{> >x = 0;> >y = 1;> >return> b;> >}> >// To store results> >// of recursive call> >let gcd = gcdExtended(b % a,> >a, x, y);> >// Update x and y using> >// results of recursive> >// call> >x = y - (b / a) * x;> >y = x;> >return> gcd;> }> // Driver Code> let x = 0;> let y = 0;> let a = 35;> let b = 15;> let g = gcdExtended(a, b, x, y);> document.write(>'gcd('> + a);> document.write(>', '> + b +>')'>);> document.write(>' = '> + g);> > |
>
>
Izhod:
gcd(35, 15) = 5>
Časovna zapletenost: O(log N)
Pomožni prostor: O(log N)
Kako deluje razširjeni algoritem?
Kot je razvidno zgoraj, sta x in y rezultata za vnosa a in b,
a.x + b.y = gcd —-(1)
In x1in y1so rezultati za vnosa b%a in a
(b%a).x1+ a.y1= gcd
Ko damo b%a = (b – (?b/a?).a) zgoraj,
sledimo. Upoštevajte, da ?b/a? je nadstropje (b/a)(b – (?b/a?).a).x1+ a.y1= gcd
Zgornjo enačbo lahko zapišemo tudi kot spodaj
b.x1+ a.(in1– (?b/a?).x1) = gcd —(2)
Po primerjavi koeficientov 'a' in 'b' v (1) in
(2), dobimo naslednje,
x = y1– ?b/a? * x1
y = x1
Kako je uporaben razširjeni algoritem?
Razširjeni evklidski algoritem je še posebej uporaben, kadar sta a in b enako praštevilna (ali je gcd 1). Ker je x modularni multiplikativni inverz od a po modulu b in je y modularni multiplikativni inverz od b po modulu a. Zlasti izračun modularnega multiplikativnega inverza je bistven korak v metodi šifriranja z javnim ključem RSA.
