logo

TechCodeview

Razlika med razvrščanjem z vstavljanjem in razvrščanjem po izboru

Razvrščanje z vstavljanjem in razvrščanje z izborom sta dva priljubljena algoritma za razvrščanje, njuna glavna razlika pa je v tem, kako izbirata in postavljata elemente v razvrščeno zaporedje.

Izbor Razvrsti:

  1. Pri izbirnem razvrščanju je vhodna matrika razdeljena na dva dela: razvrščeni del in nesortirani del.
  2. Algoritem vedno znova najde najmanjši element v nesortiranem delu in ga zamenja s skrajno levim elementom nesortiranega dela ter tako razširi razvrščeni del za en element.
  3. Razvrščanje izbire ima v vseh primerih časovno zahtevnost O(n^2).

Razvrstitev vstavljanja:

  1. Pri razvrščanju z vstavljanjem je tudi vhodna matrika razdeljena na dva dela: razvrščeni del in nesortirani del.
    Algoritem pobere element iz nerazvrščenega dela in ga postavi na pravilno mesto v razvrščenem delu, pri čemer premakne večje elemente za eno mesto v desno.
    Razvrščanje z vstavljanjem ima v najslabšem primeru časovno zapletenost O(n^2), vendar lahko deluje bolje na delno razvrščenih nizih, pri čemer je najboljša časovna zapletenost O(n).
    Glavne razlike:
  2. Izbirno razvrščanje skenira nerazvrščen del, da najde najmanjši element, medtem ko razvrščanje z vstavljanjem pregleda razvrščeni del, da najde pravilen položaj za postavitev elementa.
    Razvrščanje z izbiro zahteva manj zamenjav kot razvrščanje z vstavljanjem, vendar več primerjav.
    Razvrščanje z vstavljanjem je učinkovitejše od izbirnega razvrščanja, ko je vhodna matrika delno razvrščena ali skoraj razvrščena, medtem ko izbirno razvrščanje deluje bolje, ko je matrika močno nerazvrščena.
    Če povzamemo, imata oba algoritma podobno časovno zahtevnost, vendar se njune metode izbire in umestitve razlikujejo. Izbira med njimi je odvisna od značilnosti vhodnih podatkov in specifičnih zahtev obravnavanega problema.

Prednosti razvrščanja z vstavljanjem:

  1. Preprosto in enostavno za razumevanje in izvajanje.
  2. Učinkovito za majhne nize podatkov ali skoraj razvrščene podatke.
  3. Algoritem za razvrščanje na mestu, kar pomeni, da ne potrebuje dodatnega pomnilnika.
  4. Stabilen algoritem razvrščanja, kar pomeni, da ohranja relativni vrstni red enakih elementov v vhodni matriki.

Slabosti razvrščanja z vstavljanjem:

  1. Neučinkovito za velike nabore podatkov ali obratno urejene podatke, z najslabšim možnim časovnim zapletom O(n^2).
  2. Razvrščanje vstavljanja ima veliko zamenjav, kar lahko upočasni delo na sodobnih računalnikih.

Prednosti Selection Sort:

  1. Preprosto in enostavno za razumevanje in izvajanje.
  2. Učinkovito za majhne nize podatkov ali skoraj razvrščene podatke.
  3. Algoritem za razvrščanje na mestu, kar pomeni, da ne potrebuje dodatnega pomnilnika.

Slabosti Selection Sort:

  1. Neučinkovito za velike nize podatkov, z najslabšo časovno kompleksnostjo O(n^2).
  2. Izbirno razvrščanje ima veliko primerjav, kar lahko upočasni delo na sodobnih računalnikih.
  3. Nestabilen algoritem razvrščanja, kar pomeni, da morda ne vzdržuje relativnega vrstnega reda enakih elementov v vhodni matriki.

V tem članku bomo razpravljali o razliki med razvrščanjem vstavljanja in razvrščanjem izbire:



Razvrstitev vstavljanja je preprost algoritem za razvrščanje, ki deluje podobno kot razvrščanje igralnih kart v vaših rokah. Niz je praktično razdeljen na razvrščeni in nesortirani del. Vrednosti iz nesortiranega dela so izbrane in postavljene na pravilno mesto v razvrščenem delu.

Algoritem:
Če želite razvrstiti matriko velikosti n v naraščajočem vrstnem redu:

  • Iteracija od arr[1] do arr[n] po matriki.
  • Primerjajte trenutni element (ključ) z njegovim predhodnikom.
  • Če je ključni element manjši od svojega predhodnika, ga primerjajte s prejšnjimi elementi. Premaknite večje elemente za en položaj navzgor, da naredite prostor za zamenjani element.

Spodaj je slika za ponazoritev razvrščanja vstavljanja:



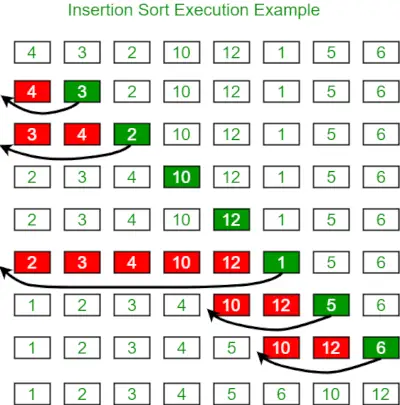
vstavljanje-vrsta

Spodaj je program za isto:

C++






// C++ program for the insertion sort> #include> using> namespace> std;> // Function to sort an array using> // insertion sort> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i = 1; i key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> ključ) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = ključ; } } // Funkcija za tiskanje matrike velikosti N void printArray(int arr[], int n) { int i; // Natisni matriko za (i = 0; i cout<< arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 12, 11, 13, 5, 6 }; int N = sizeof(arr) / sizeof(arr[0]); // Function Call insertionSort(arr, N); printArray(arr, N); return 0; }> 

>

>

Java




// Java program for the above approach> import> java.util.*;> class> GFG> {> > // Function to sort an array using> // insertion sort> static> void> insertionSort(>int> arr[],>int> n)> {> >int> i, key, j;> >for> (i =>1>; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> ključ) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = ključ; } } // Funkcija za tiskanje matrike velikosti N static void printArray(int arr[], int n) { int i; // Natisni matriko za (i = 0; i System.out.print(arr[i] + ' '); } System.out.println(); } // Koda gonilnika public static void main(String[ ] arrs) { int arr[] = { 12, 11, 13, 5, 6 }; // Funkcija InsertionSort(arr, N); To kodo je prispeval code_hunt> 

>

>

Python3




# Python 3 program for the insertion sort> # Function to sort an array using> # insertion sort> def> insertionSort(arr, n):> >i>=> 0> >key>=> 0> >j>=> 0> >for> i>in> range>(>1>,n,>1>):> >key>=> arr[i]> >j>=> i>-> 1> ># Move elements of arr[0..i-1],> ># that are greater than key to> ># one position ahead of their> ># current position> >while> (j>>=> 0> and> arr[j]>ključ):> >arr[j>+> 1>]>=> arr[j]> >j>=> j>-> 1> >arr[j>+> 1>]>=> key> # Function to print an array of size N> def> printArray(arr, n):> >i>=> 0> ># Print the array> >for> i>in> range>(n):> >print>(arr[i],end>=> ' '>)> >print>(>' '>,end>=> '')> # Driver Code> if> __name__>=>=> '__main__'>:> >arr>=> [>12>,>11>,>13>,>5>,>6>]> >N>=> len>(arr)> ># Function Call> >insertionSort(arr, N)> >printArray(arr, N)> > ># This code is contributed by bgangwar59.> 

>

>

C#




// C# program for the above approach> using> System;> class> GFG> {> >// Function to sort an array using> >// insertion sort> >static> void> insertionSort(>int>[] arr,>int> n)> >{> >int> i, key, j;> >for> (i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> ključ) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = ključ; } } // Funkcija za tiskanje matrike velikosti N static void printArray(int[] arr, int n) { int i; // Natisni matriko za (i = 0; i { Console.Write(arr[i] + ' '); } Console.WriteLine(); } // Koda gonilnika static public void Main() { int[] arr = new int[] { 12, 11, 13, 5, 6 }; int N = arr.Length; // Funkcija InsertionSort(arr, N); printArray(arr, N); // Ta koda je prispeval Dharanendra L V> 

>

>

Javascript




> // JavaScript program for the above approach> // Function to sort an array using> // insertion sort> function> insertionSort(arr,n)> {> >let i, key, j;> >for> (i = 1; i { key = arr[i]; j = i - 1; // Move elements of arr[0..i-1], // that are greater than key to // one position ahead of their // current position while (j>= 0 && arr[j]> ključ) { arr[j + 1] = arr[j]; j = j - 1; } arr[j + 1] = ključ; } } // Funkcija za tiskanje matrike velikosti N function printArray(arr,n) { let i; // Natisni matriko za (i = 0; i document.write(arr[i] + ' '); } document.write(' '); } // Koda gonilnika let arr=[12, 11 , 13, 5, 6]; let N = arr.length; // Pokliči funkcijo insertionSort(arr, N); // To kodo prispeva avanitrachhadiya2155> 

>

>

Izhod: 

5 6 11 12 13>

The izbirna vrsta algoritem razvrsti matriko tako, da večkrat poišče najmanjši element (glede na naraščajoči vrstni red) iz nerazvrščenega dela in ga postavi na začetek. Algoritem vzdržuje dve podnitri v dani matriki.

  • Podmatrika je že razvrščena.
  • Preostala podmatrika je nerazvrščena.

V vsaki ponovitvi izbirnega razvrščanja se najmanjši element (glede na naraščajoči vrstni red) iz nerazvrščene podmatrike izbere in premakne v razvrščeno podmatrico.

Spodaj je primer, ki pojasnjuje zgornje korake:

arr[] = 64 25 12 22 11 // Find the minimum element in arr[0...4] // and place it at beginning 11  25 12 22 64 // Find the minimum element in arr[1...4] // and place it at beginning of arr[1...4] 11 12  25 22 64 // Find the minimum element in arr[2...4] // and place it at beginning of arr[2...4] 11 12 22  25 64 // Find the minimum element in arr[3...4] // and place it at beginning of arr[3...4] 11 12 22 25  64>

Spodaj je program za isto:

C++




// C++ program for implementation of> // selection sort> #include> using> namespace> std;> // Function to swap two number> void> swap(>int>* xp,>int>* yp)> {> >int> temp = *xp;> >*xp = *yp;> >*yp = temp;> }> // Function to implement the selection> // sort> void> selectionSort(>int> arr[],>int> n)> {> >int> i, j, min_idx;> >// One by one move boundary of> >// unsorted subarray> >for> (i = 0; i // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element swap(&arr[min_idx], &arr[i]); } } // Function to print an array void printArray(int arr[], int size) { int i; for (i = 0; i cout << arr[i] << ' '; } cout << endl; } // Driver Code int main() { int arr[] = { 64, 25, 12, 22, 11 }; int n = sizeof(arr) / sizeof(arr[0]); // Function Call selectionSort(arr, n); cout << 'Sorted array: '; // Print the array printArray(arr, n); return 0; }> 

>

>

Java




// Java program for implementation of> // selection sort> import> java.util.*;> class> GFG> {> // Function to implement the selection> // sort> static> void> selectionSort(>int> arr[],>int> n)> {> >int> i, j, min_idx;> >// One by one move boundary of> >// unsorted subarray> >for> (i =>0>; i 1; i++) { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int arr[], int size) { int i; for (i = 0; i System.out.print(arr[i]+ ' '); } System.out.println(); } // Driver Code public static void main(String[] args) { int arr[] = { 64, 25, 12, 22, 11 }; int n = arr.length; // Function Call selectionSort(arr, n); System.out.print('Sorted array: '); // Print the array printArray(arr, n); } } // This code is contributed by aashish1995> 

>

>

Python3




# Python3 program for implementation of> # selection sort> # Function to implement the selection> # sort> def> selectionSort(arr, n):> ># One by one move boundary of> ># unsorted subarray> >for> i>in> range>(n>-> 1>):> ># Find the minimum element> ># in unsorted array> >min_idx>=> i> >for> j>in> range>(i>+> 1>, n):> >if> (arr[j] min_idx = j # Swap the found minimum element # with the first element arr[min_idx], arr[i] = arr[i], arr[min_idx] # Function to print an array def printArray(arr, size): for i in range(size): print(arr[i], end = ' ') print() # Driver Code if __name__ == '__main__': arr = [64, 25, 12, 22, 11] n = len(arr) # Function Call selectionSort(arr, n) print('Sorted array: ') # Print the array printArray(arr, n) # This code is contributed by ukasp> 

>

>

C#


foreach java



// C# program for implementation of> // selection sort> using> System;> public> class> GFG> {> // Function to implement the selection> // sort> static> void> selectionSort(>int> []arr,>int> n)> {> >int> i, j, min_idx;> >// One by one move boundary of> >// unsorted subarray> >for> (i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for (j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element int temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array static void printArray(int []arr, int size) { int i; for (i = 0; i Console.Write(arr[i]+ ' '); } Console.WriteLine(); } // Driver Code public static void Main(String[] args) { int []arr = { 64, 25, 12, 22, 11 }; int n = arr.Length; // Function Call selectionSort(arr, n); Console.Write('Sorted array: '); // Print the array printArray(arr, n); } } // This code is contributed by gauravrajput1> 

>

>

Javascript




> // Javascript program for implementation of> // selection sort> // Function to implement the selection> // sort> function> selectionSort(arr, n)> {> >let i, j, min_idx;> > >// One by one move boundary of> >// unsorted subarray> >for>(i = 0; i { // Find the minimum element // in unsorted array min_idx = i; for(j = i + 1; j if (arr[j] min_idx = j; // Swap the found minimum element // with the first element let temp = arr[min_idx]; arr[min_idx]= arr[i]; arr[i] = temp; } } // Function to print an array function printArray(arr, size) { let i; for(i = 0; i { document.write(arr[i] + ' '); } document.write(' '); } // Driver Code let arr = [ 64, 25, 12, 22, 11 ]; let n = arr.length; // Function Call selectionSort(arr, n); document.write('Sorted array: '); // Print the array printArray(arr, n); // This code is contributed by rag2127> 

>

>

Izhod: 

Sorted array: 11 12 22 25 64>

Tabelarična razlika med razvrščanjem vstavljanja in razvrščanjem izbire:

Razvrščanje vstavljanja Izbor Razvrsti
1. Vstavi vrednost v predhodno razvrščeno matriko, da razvrsti niz vrednosti v matriki. Poišče najmanjše/največje število s seznama in ga razvrsti v naraščajočem/padajočem vrstnem redu.
2. Je stabilen algoritem za razvrščanje. Je nestabilen algoritem razvrščanja.
3. Najboljša časovna kompleksnost je Ω(N), ko je niz že v naraščajočem vrstnem redu. Ima Θ(N2) v najslabšem in povprečnem primeru. V najboljšem primeru, najslabšem primeru in povprečnem izboru je kompleksnost Θ(N2).
4. Število primerjalnih operacij, izvedenih v tem algoritmu razvrščanja, je manjše od izvedene zamenjave. Število primerjalnih operacij, izvedenih v tem algoritmu razvrščanja, je večje od izvedenih zamenjav.
5. Je učinkovitejši od izbirnega razvrščanja. Je manj učinkovit kot razvrščanje z vstavljanjem.
6. Tukaj je element vnaprej znan in iščemo pravilno lego, da jih postavimo. Mesto, kamor bomo postavili element, je predhodno znano, iščemo element, ki ga bomo vstavili na to mesto.
7.

Razvrščanje vstavljanja se uporablja, kadar:

  • Matrika ima majhno število elementov
  • Razvrstiti je treba le še nekaj elementov

Izbirno razvrščanje se uporablja, ko

  • Majhen seznam je treba razvrstiti
  • Stroški menjave niso pomembni
  • Preverjanje vseh elementov je obvezno
  • Stroški pisanja v pomnilnik so pomembni kot pri bliskovnem pomnilniku (število zamenjav je O(n) v primerjavi z O(n2) mehurčkov)
8. Razvrščanje vstavljanja je prilagodljivo, tj. učinkovito za nabore podatkov, ki so že v bistvu razvrščeni: časovna kompleksnost je O(kn) ko vsak element v vhodu ne presega k mesta stran od svojega razvrščenega položaja Izbirno razvrščanje je algoritem za razvrščanje s primerjavo na mestu