Verjetnost kart je verjetnost dogodkov, ki vključujejo komplet igralnih kart. Kot vemo, je verjetnost ena izmed pomembnih tem matematike, ki se ukvarja z izračunom možnosti katerega koli dogodka. Preprosto povedano, verjetnost kart je del verjetnosti, v katerem najdemo verjetnost, da potegnemo karto iz kompleta kart. V tem članku bomo spoznali verjetnost kart z vsemi podrobnostmi o grafikonu verjetnosti kart, verjetnosti igralnih kart, kako najti verjetnost kart in rešili primere verjetnosti kart. Začnimo z učenjem na temo verjetnosti kartice.
Kaj je verjetnost?
Verjetnost je veja matematike, ki preučuje možnosti, da se kateri koli dogodek zgodi ali ne. Matematično ni nič drugega kot razmerje med številom ugodnih izidov in skupnim številom izidov (vzorčni prostor) za dogodek.
Nekateri primeri verjetnosti iz resničnega življenja so:
- Igranje iger s kartami, da ugotovite verjetnost zmage ali izgube igre.
- Vremenska napoved, napovedati dež.
- Rezultati volitev, da se ugotovi, ali bo kandidat zmagal ali izgubil.
- Rezultati izpita, da se ugotovi, ali bo kandidat opravil ali ne.
Formula verjetnosti
Če je E dogodek z vzorčnim prostorom S in je število ugodnih izidov n(E), potem je verjetnost dogodka E, tj. P(E), podana z:
P(E) = n(E) / n(S)
Kaj je verjetnost kartice?
Verjetnost, da povlečete karto ali zbirko kart iz kompleta, se imenuje verjetnost karte. Z enostavnimi besedami se verjetnost, povezana z igranjem kart, imenuje verjetnost kart. Ker je to vrsta verjetnosti, je vedno med 0 in 1. Na primer, če moramo poiskati verjetnost, da potegnemo asa iz kompleta kart, je 4/52 = 1/13 [Ker obstajajo 4 asi v kompletu 52 kart].
Špil kart v verjetnosti
Komplet kart je zbirka 52 kart, za katere se zdi, da obstajajo že tisoče let. Za špil kart ali igralne karte velja, da izvirajo iz Indije ali Kitajske, prvi dokumentirani dokaz o teh kartah je bil najden v 9.thstoletja na Kitajskem v času dinastije Tang. Te karte so bile podobne sodobnim kartam in prav tako razdeljene na štiri barve, vendar sta ime in simbol teh barv drugačna, tj. kovanci, nizi kovancev, miriade in miriade desetic.
V sodobnem času so te karte v različnih oblikah in so razdeljene v štiri barve, in sicer pik (♠), tref (♣), srce (❤) in karo (◆). Za posamezno izbrano karto je vzorčni prostor 52, tj. skupno število izidov za posamezno izbrano karto iz kompleta je 52.
n(S) za komplet kart = 52
Vrste kart v krovu
Vsak komplet kart je mogoče razvrstiti na več načinov, nekateri parametri, po katerih je mogoče razvrstiti karte, so:
- Na podlagi barv
- Na podlagi Suits
Razumejmo to razvrstitev podrobno na naslednji način:
Na podlagi barv
Glede na barve lahko komplet kart razvrstimo v dve kategoriji,
- Rdeči kartoni
- Črne karte
Skupaj 52 kart je enakomerno razdeljenih na rdeče in črne karte, kar pomeni, da je v kompletu 26 rdečih kart in 26 črnih kart.
Na podlagi Suits
V kompletu kart so štiri barve, ki so:
- Srčki (❤)
- Diamanti (◆)
- Klubi (♣)
- pik (♠)
Poleg teh obstaja še ena klasifikacija kart, ki temelji na rangu kart:
- As
- Številčne kartice
- Obrazne kartice
As
As je ena taka karta, ki je glede na igro najpomembnejša ali najmanj pomembna. Na tej karti je napisano A in vsaka barva ima eno takšno karto, tj. štiri karte asov.
Številčne kartice
Od 2 do 10 je 9 kart na barvo, torej je skupaj 36 takih kart.
Obrazne kartice
Obrazne kartice, kot že ime pove, vsebujejo figuro ali obraz figure na kartici. Obstajajo tri karte vsake barve, tj Jack, Queen, King. Tako je skupaj 12 obraznih kart.
Vse te razvrstitve si lahko ogledate v naslednji tabeli.
| Špil kart (52 kart) | ||||
|---|---|---|---|---|
| Barvne karte | Črne karte (26 kart) | Rdeči kartoni (26 kartonov) | ||
| Obleke | Pik (13 kart) | Klub (13 kart) | Srce (13 kart) | Diamant (13 kart) |
| Obrazne kartice (12 kart v kompletu in 3 karte v vsaki barvi) | K (kralj) | K (kralj) | K (kralj) | K (kralj) |
| Q (kraljica) | Q (kraljica) | Q (kraljica) | Q (kraljica) | |
| J (Jack) | J (Jack) | J (Jack) | J (Jack) | |
| Številčne kartice (36 kart v kompletu in 9 kart v barvi) | 10 | 10 | 10 | 10 |
| 9 | 9 | 9 | 9 | |
| 8 | 8 | 8 | 8 | |
| 7 | 7 | 7 | 7 | |
| 6 | 6 | 6 | 6 | |
| 5 | 5 | 5 | 5 | |
| 4 | 4 | 4 | 4 | |
| 3 | 3 | 3 | 3 | |
| 2 | 2 | 2 | 2 | |
| As karte (4 karte v kompletu in 1 karta v barvi) | A (as) | A (as) | A (as) | A (as) |
Tabela kompleta kart
Naslednja tabela predstavlja razvrstitev kompleta igralnih kart:
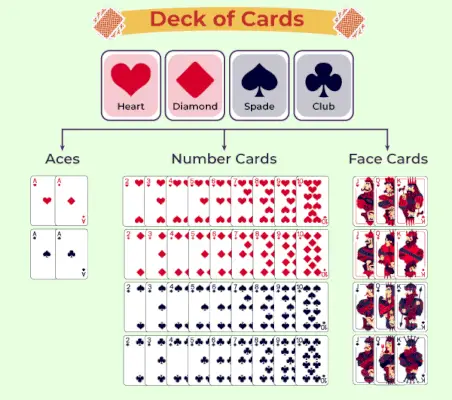
Verjetnost igralne karte
Nekateri pogosti dogodki v verjetnosti kart so obravnavani v naslednji tabeli:
| Dogodek E za vlečenje karte | Verjetnost P(E) |
|---|---|
| As | P(E) = 4/52 = 1/13 |
| Kralj | P(E) = 4/52 = 1/13 |
| Številčna kartica | P(E) = 36/52 = 9/13 |
| Obrazna kartica | P(E) = 12/52 = 3/13 |
| Pikova karta | P(E) = 13/52 = 1/4 |
| Rdeči karton | P(E) = 26/52 = 1/2 |
Kako najti verjetnost kart?
Koraki za iskanje verjetnosti dogodkov, ki vključujejo karte, so enaki kot vse druge verjetnosti, ki so podane na naslednji način:
Korak 1: Najprej poiščite število ugodnih izidov iz danega vprašanja.
2. korak: Nato poiščite skupno število rezultatov.
3. korak: Uporabite formulo verjetnosti, da poiščete verjetnost karte.
Primer: Kakšna je verjetnost, da iz kompleta kart potegnemo asa?
odgovor:
Tu je E dogodek izvlečenja karte asa
Skupno število izidov v kompletu n(S) = 52
Število ugodnih izidov = n(E) = vlečenje karte asov iz kompleta = 4 (v enem kompletu so 4 karte asov)
P(E) = n(E) / n(S) = 4 / 52
P(E) = 1/13
Verjetnost, da izvlečete karto asa = 1/13
Primeri vprašanj o verjetnosti karte
Problem 1: Kakšna je verjetnost, da iz kompleta kart potegnemo naslednje karte?
(i) pik
(ii) črni karton
(iii) številsko kartico
rešitev:
(i) Tukaj je E dogodek vlečenja pikove karte
Skupno število izidov v kompletu n(S) = 52
Število ugodnih izidov = n(E) = vlečenje pikove karte iz kompleta = 13 (v 1 kompletu je 13 kart vsake barve)
P(E) = n(E) / n(S) = 13 / 52
P(E) = 1/4
Verjetnost, da izvlečete pik = 1/4
(ii) Tukaj je E dogodek črne karte
Skupno število izidov v kompletu n(S) = 52
Število ugodnih izidov = n(E) = vlečenje črne karte iz krova = 26 (v enem kompletu je 26 črnih kart)
P(E) = n(E) / n(S) = 26 / 52
P(E) = 1/2
Verjetnost, da izvlečete črno karto = 1/2
(iii) Tukaj je E dogodek žrebanja kartice s številko
Skupno število izidov v kompletu n(S) = 52
Število ugodnih izidov = n(E) = vlečenje številske karte iz kompleta = 36 (v 1 kompletu je 36 številskih kart)
P(E) = n(E) / n(S) = 36 / 52
P(E) = 9/13
Verjetnost, da boste izvlekli karto s številko = 9/13
Problem 2: Kakšna je verjetnost, da iz kompleta kart potegnemo naslednje karte?
(i) Kralj ali črna karta
(ii) Rdeča karta in as
rešitev:
(i) Tukaj je E dogodek izvlečenja kralja ali črne karte
Skupno število izidov v kompletu n(S) = 52
Število ugodnih izidov = n(E) = vlečenje kralja ali črne karte iz krova = 26 + 2 = 28 (v 1 kompletu je 26 črnih kart, od katerih sta 2 kralja in preostala 2 črna kralja)
P(E) = n(E) / n(S) = 28 / 52
P(E) = 7/13
Verjetnost, da izvlečete kralja ali črno karto = 7/13
(ii) Tukaj je E dogodek izvlečenja rdeče karte in asa
Skupno število izidov v kompletu n(S) = 52
Število ugodnih izidov = n(E) = vlečenje rdeče karte in karte asa iz kompleta = 2 (obstaja 26 rdečih kart, od katerih sta 2 karti asa)
Glede na vprašanje mora biti izvlečena karta rdeča in oba asa. Zato je n(E) = 2
P(E) = n(E) / n(S) = 2 / 52
P(E) = 1/26
Verjetnost, da izvlečete rdečo karto in asa = 1 / 26
Problem 3: Kakšna je verjetnost, da iz kompleta kart potegnemo naslednje karte?
(i) Neklubska kartica
(ii) Kartica brez obraza
rešitev:
(i) Tukaj je E dogodek izvlečenja neklubske karte
Skupno število izidov v kompletu n(S) = 52
Število ugodnih izidov = n(E) = vlečenje neklubske karte iz kompleta = 39 (v 1 kompletu je 13 palic, nešpil = 52 – 13 = 39)
P(E) = n(E) / n(S) = 39 / 52
P(E) = 3/4
Verjetnost, da izvlečete neklubsko karto = 3/4
(ii) Tukaj je E dogodek žrebanja kartice brez obraza
Skupno število izidov v kompletu n(S) = 52
Število ugodnih izidov = n(E) = vlečenje karte brez obraza iz kompleta = 40 (v 1 kompletu je 12 kart z obrazom, brez krova = 52 – 12 = 40)
P(E) = n(E) / n(S) = 40/52
P(E) = 10/13
Verjetnost, da izvlečete neklubsko karto = 10/13
Problem 4: Kakšna je verjetnost, da izvlečete karto, ki ni niti rdeča niti obrazna?
rešitev:
Tu je E dogodek izvlečenja niti rdeče niti obrazne karte
Skupno število izidov v kompletu n(S) = 52
Število ugodnih izidov = n(E) = iz kompleta ni potegnjena niti rdeča niti obrazna karta.
Skupaj rdečih kartonov = 26
V kompletu je skupno 12 kart z obrazom, vendar je 6 kart z rdečim obrazom že odstranjenih. Torej preostale obrazne karte = 12 – 6 = 6
n(E) = 26 + 6 = 32
P(E) = n(E) / n(S) = 32/52
P(E) = 8/13
Verjetnost, da izvlečete ne rdečo ne obrazno karto = 8 / 13
Problem 5: Kakšna je verjetnost, da iz kompleta kart z zamenjavo potegnemo dve karti, če je prva karta srce, druga pa karo?
rešitev:
Verjetnost, da izvlečete prvo karto kot srce = 13/52
Po izvleku prve karte se ta odstrani.
Verjetnost, da izvlečete drugo karto kot karo = 13/51
Verjetnost, da izvlečete prvo karto kot srce in drugo kot diamant = (13 / 52) × (13 / 51)
ubežni znak javaVerjetnost, da izvlečete prvo karto kot srce in drugo kot karo = 13/204
Pogosta vprašanja o verjetnosti kartice
1. Kaj je verjetnost karte?
Verjetnost, da potegnemo karto iz kompleta kart, se imenuje verjetnost kart.
2. Naštejte vrste barv v kompletu kart.
V kompletu kart so štiri vrste barv. To so:
- srčki
- Diamanti
- Pik
- Klubi
3. Kakšen je vzorčni prostor za komplet kart, ko se ena karta izvleče iz kompleta?
Vzorčni prostor za komplet kart, ko je izvlečena ena karta, vsebuje 52 rezultatov.
4. Napišite formulo za iskanje verjetnosti.
Formula za iskanje verjetnosti je podana z:
Verjetnost dogodka = število ugodnih dogodkov / skupno število izidov
ALI
P(E) = n(E) / n(S)
5. Koliko obraznih kart je prisotnih v kompletu kart?
V kompletu kart je 12 obraznih kart.
