Pred razumevanjem B drevo in B+ drevo razlike, bi morali poznati drevo B in drevo B+ ločeno.
Kaj je drevo B?
B drevo je samouravnoteženo drevo in je m-smerno drevo, kjer m definira vrstni red drevesa. Btree je posplošitev Binarno iskalno drevo v katerem ima lahko vozlišče več kot en ključ in več kot dva otroka, odvisno od vrednosti m . V drevesu B so podatki podani v razvrščenem vrstnem redu z nižjimi vrednostmi v levem poddrevesu in višjimi vrednostmi v desnem poddrevesu.
java pretvori char v int
Lastnosti drevesa B
Lastnosti drevesa B so naslednje:
- V drevesu B morajo biti vsa listna vozlišča na isti ravni, medtem ko so lahko v primeru binarnega drevesa listna vozlišča na različnih ravneh.
Razumejmo to lastnost na primeru.
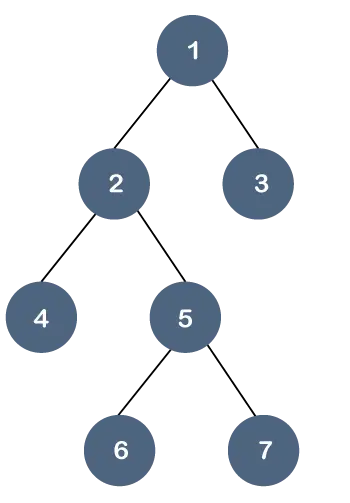
V zgornjem drevesu vsa vozlišča listov niso na isti ravni, vendar imajo največ dva otroka. Zato lahko rečemo, da je zgornje drevo a binarno drevo vendar ne drevo B.
- Če ima Btree vrstni red m, ima lahko vsako vozlišče največ m V primeru najmanjših otrok imajo listna vozlišča nič otrok, korensko vozlišče ima dva otroka, notranja vozlišča pa imajo zgornjo mejo m/2.
- Vsako vozlišče ima lahko največ (m-1) ključev. Na primer, če je vrednost m 5, potem je največja vrednost ključev 4.
- Korensko vozlišče ima najmanj en ključ, medtem ko imajo vsa druga vozlišča razen korenskega (zgornja meja m/2 minus - 1) najmanjše ključe.
- Če izvedemo vstavljanje v drevo B, potem je vozlišče vedno vstavljeno v listno vozlišče.
Recimo, da želimo ustvariti drevo B reda 3 z vstavljanjem vrednosti od 1 do 10.
Korak 1: Najprej ustvarimo vozlišče z 1 vrednostjo, kot je prikazano spodaj:

2. korak: Naslednji element je 2, ki pride za 1, kot je prikazano spodaj:

3. korak: Naslednji element je 3 in je vstavljen za 2, kot je prikazano spodaj:

Ker vemo, da ima lahko vsako vozlišče največ 2 ključa, bomo to vozlišče razdelili skozi srednji element. Srednji element je 2, zato se premakne k svojemu staršu. Vozlišče 2 nima nadrejenega, zato bo postalo korensko vozlišče, kot je prikazano spodaj:

4. korak: Naslednji element je 4. Ker je 4 večje od 2 in 3, bo dodan za 3, kot je prikazano spodaj:

5. korak: Naslednji element je 5. Ker je 5 večje od 2, 3 in 4, bo dodan za 4, kot je prikazano spodaj:

Ker vemo, da ima lahko vsako vozlišče največ 2 ključa, bomo to vozlišče razdelili skozi srednji element. Srednji element je 4, zato se premakne k svojemu staršu. Nadrejeni je vozlišče 2; zato bo 4 dodano za 2, kot je prikazano spodaj:

6. korak: Naslednji element je 6. Ker je 6 večje od 2, 4 in 5, bo 6 prišlo za 5, kot je prikazano spodaj:

7. korak: Naslednji element je 7. Ker je 7 večje od 2, 4, 5 in 6, bo 7 prišlo za 6, kot je prikazano spodaj:

Ker vemo, da ima lahko vsako vozlišče največ 2 ključa, bomo to vozlišče razdelili skozi srednji element. Srednji element je 6, zato se premakne k svojemu nadrejenemu, kot je prikazano spodaj:

Toda 6 ni mogoče dodati po 4, ker ima lahko vozlišče največ 2 ključa, zato bomo to vozlišče razdelili skozi srednji element. Srednji element je 4, zato se premakne k svojemu staršu. Ker vozlišče 4 nima nadrejenega, bo vozlišče 4 postalo korensko vozlišče, kot je prikazano spodaj:

Kaj je drevo B+?
The B+ drevo je znano tudi kot napredno samouravnoteženo drevo, ker ima vsaka pot od korena drevesa do lista drevesa enako dolgo. Tu enaka dolžina pomeni, da se vsa listna vozlišča pojavljajo na isti ravni. Ne bo se zgodilo, da bi se nekateri listni vozli pojavili na tretji ravni, nekateri pa na drugi ravni.
Drevesni indeks B+ velja za večnivojski indeks, vendar drevesna struktura B+ ni podobna zaporednim datotekam večnivojskega indeksa.
Zakaj se uporablja drevo B+?
Drevo B+ se uporablja za zelo učinkovito shranjevanje zapisov s shranjevanjem zapisov na indeksiran način z uporabo drevesne indeksirane strukture B+. Zaradi večnivojskega indeksiranja postane dostop do podatkov hitrejši in lažji.
Struktura vozlišča drevesa B+
Struktura vozlišča drevesa B+ vsebuje kazalce in ključne vrednosti, prikazane na spodnji sliki:

Kot lahko opazimo v zgornji strukturi drevesnega vozlišča B+, vsebuje n-1 ključnih vrednosti (k1do kn-1) in n kazalcev (str1na strn).
Vrednosti iskalnih ključev, ki so postavljene v vozlišče, se hranijo v razvrščenem vrstnem redu. Torej, če i
Omejitev na različne vrste vozlišč
Naj bo 'b' vrstni red drevesa B+.
Nelistno vozlišče
Naj 'm' predstavlja število otrok vozlišča, potem lahko razmerje med vrstnim redom drevesa in številom otrok predstavimo kot:

Naj k predstavlja vrednosti iskalnih ključev. Razmerje med vrstnim redom drevesa in iskalnim ključem lahko predstavimo kot:
Ker vemo, da je število kazalcev enako vrednostim iskalnega ključa plus 1, ga lahko matematično zapišemo kot:
Število kazalcev (ali otrok) = število iskalnih tipk + 1
Zato bi bilo največje število kazalcev 'b', najmanjše število kazalcev pa bi bila zgornja funkcija b/2.
Listni vozel
Listno vozlišče je vozlišče, ki se pojavi na zadnji ravni drevesa B+, in vsako listno vozlišče uporablja samo en kazalec za povezavo med seboj, da zagotovi zaporedni dostop na ravni lista.
V listnem vozlišču je največje število otrok:

Največje število iskalnih ključev je:

Korensko vozlišče
Največje število otrok v primeru korenskega vozlišča je: b
Najmanjše število otrok je: 2
negacijska diskretna matematika
Posebni primeri v drevesu B+
1. primer: Če je korensko vozlišče edino vozlišče v drevesu. V tem primeru korensko vozlišče postane listno vozlišče.
V tem primeru je največje število otrok 1, to je samo korensko vozlišče, medtem ko je najmanjše število otrok b-1, kar je enako kot listno vozlišče.
Predstavitev listnega vozla v drevesu B+

Na zgornji sliki '.' predstavlja kazalec, medtem ko so 10, 20 in 30 ključne vrednosti. Kazalec vsebuje naslov, na katerem je shranjena vrednost ključa, kot je prikazano na zgornji sliki.
Primer B+ drevesa

Na zgornji sliki vozlišče vsebuje tri ključne vrednosti, tj. 9, 16 in 25. Kazalec, ki se pojavi pred 9, vsebuje ključne vrednosti, manjše od 9, ki jih predstavlja kjaz. Kazalec, ki se pojavi pred 16, vsebuje ključne vrednosti, večje ali enake 9, vendar manjše od 16, ki jih predstavlja kj. Kazalec, ki se pojavi pred 25, vsebuje ključne vrednosti, večje ali enake 16, vendar manjše od 25, ki jih predstavlja kn.
Razlike med drevesom B in drevesom B+

Med drevesom B in drevesom B+ so naslednje razlike:
| B drevo | B+ drevo |
|---|---|
| V drevesu B so vsi ključi in zapisi shranjeni v notranjih in listnih vozliščih. | V drevesu B+ so ključi indeksi, shranjeni v notranjih vozliščih, zapisi pa so shranjeni v listnih vozliščih. |
| V drevesu B ključev ni mogoče večkrat shraniti, kar pomeni, da ni podvajanja ključev ali zapisov. | V drevesu B+ lahko pride do redundance pri pojavljanju ključev. V tem primeru so zapisi shranjeni v listnih vozliščih, medtem ko so ključi shranjeni v notranjih vozliščih, tako da so lahko odvečni ključi prisotni v notranjih vozliščih. |
| V drevesu B listna vozlišča med seboj niso povezana. | V drevesu B+ so listna vozlišča povezana med seboj, da zagotovijo zaporedni dostop. |
| V Btreeju iskanje ni zelo učinkovito, ker so zapisi shranjeni v listih ali notranjih vozliščih. | V drevesu B+ je iskanje zelo učinkovito oziroma hitrejše, ker so vsi zapisi shranjeni v vozliščih listov. |
| Brisanje notranjih vozlišč je zelo počasen in dolgotrajen proces, saj moramo upoštevati tudi podrejenega elementa izbrisanega ključa. | Brisanje v drevesu B+ je zelo hitro, ker so vsi zapisi shranjeni v vozliščih listov, tako da nam ni treba upoštevati podrejenega vozlišča. |
| V Btree zaporedni dostop ni mogoč. | V drevesu B+ so vsa vozlišča listov povezana med seboj preko kazalca, tako da je možen zaporedni dostop. |
| V Btree se izvede več operacij cepljenja, zaradi česar se višina poveča v primerjavi s širino, | B+ drevo ima večjo širino v primerjavi z višino. |
| V Btree ima vsako vozlišče vsaj dve veji in vsako vozlišče vsebuje nekaj zapisov, zato nam ni treba iti do listnih vozlišč, da bi dobili podatke. | V drevesu B+ notranja vozlišča vsebujejo samo kazalce, listna vozlišča pa zapise. Vsa listna vozlišča so na isti ravni, zato moramo iti do listnih vozlišč, da dobimo podatke. |
| Korensko vozlišče vsebuje vsaj 2 do m otrok, kjer je m vrstni red drevesa. | Korensko vozlišče vsebuje vsaj 2 do m otrok, kjer je m vrstni red drevesa. |
