Kot med dvema vektorjema je kot med njunima repoma in ta kot je mogoče enostavno najti z navzkrižnim produktom in pikčastim produktom vektorskih formul. Kot med dvema vektorjema je vedno med 0° in 180°.

V tem članku bomo podrobno spoznali kot med dvema vektorjema, definicijo, formule in primere.

Kaj je kot med dvema vektorjema?

Kot med dvema vektorjema je kot, ki nastane v presečišču njunih repov. Kot med dvema vektorjema je lahko oster, pravi ali top, odvisno od smeri vektorjev.

Kot med dvema vektorjema najdemo z dvema formulama:

• Uporaba pikčastega produkta vektorjev
• Uporaba navzkrižnega produkta vektorjev

To je razloženo v spodnji formuli.

Formule kota med dvema vektorjema

Kot med dvema vektorjema enostavno in najpogosteje najdemo s skalarnim produktom vektorjev.

Dva vektorja A in B

Pikasti izdelek od A in B je podan z

vec{A}.vec{B} = |A| |B| cosθ.

Posebni primeri

• Ko je kot med vektorji 0 stopinj.

To je θ = 0°

⇒ |A| |B| cosθ

⇒ |A| |B| cos0°

⇒ |A| |B| [cos0° = 1]

• Ko je kot med vektorji 180 stopinj.

⇒ |A| |B| cosθ

⇒ |A| |B| cos180°

spanje v javascriptu

⇒ – |A| |B| [cos180° = -1]

• Ko je kot med vektorji 90 stopinj.

⇒ |A| |B| cosθ

⇒ |A| |B| cos90°

⇒ |A| |B| × 0 [cos90° = 0]

⇒ 0

Formula za kot med dvema vektorjema

Kosinus kota med dvema vektorjema je enak vsoti zmnožka posameznih sestavin obeh vektorjev, deljeno z zmnožkom velikosti obeh vektorjev.

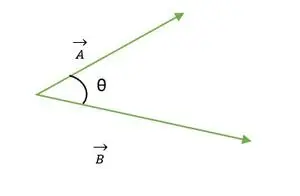
Dva vektorja A in B

vec{A}.vec{B} =| A | | B | cosθ.

cosθ=frac{vec{A}.vec{B}}B

θ= cos^-1 frac{vec{A}.vec{B}}B

V kartezični obliki,

A = A_xi + A_inj + A_zk

B= B_xi + B_inj + B_zk

cos θ =frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Lastnosti produkta Dot

• Pikčasti produkt je komutativen

vec{A}.vec{B}=vec{B}.vec{A}

• Dot izdelek je distribucijski

vec{A}.(vec{B}+vec{C})=(vec{A}.vec{B}+vec{A}.vec{C})

Kot med dvema vektorjema leži med 0 ≤ θ ≤ 180. Ko repa ali glave obeh vektorjev sovpadata, se izračuna kot med vektorjema.

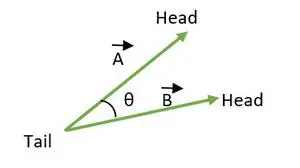
Rep sovpada

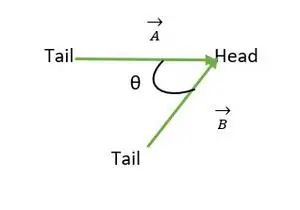
Glava sovpada

Primeri nalog Formula kota med dvema vektorjema

1. naloga: Poiščite kot med vektorjema (če tvorita enakostranični trikotnik)

• vektorja a in b
• b in c vektorja
• vektorja a in c

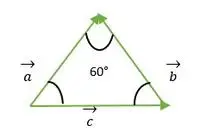
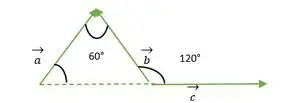
Enakostranični trikotnik, ki ga tvorijo vektorji a, b, c

rešitev:

• vektorja a in b

Pri vektorju a in b glavi obeh vektorjev sovpadata, zato je kot med vektorjem a in b enak kotu med dvema stranicama enakostraničnega trikotnika = 60°.

• vektorja b in c:

Iz zgornje slike vidimo, da glava ali rep vektorja b in c ne sovpadata drug z drugim.

Torej z uporabo lastnosti - Vektor ostane nespremenjen, če se prenaša vzporedno s samim seboj.

Vektor c je premaknjen vzporedno sam s seboj

Sedaj vidimo, da rep vektorjev b in c sovpadata drug z drugim, zato je enak zunanjemu kotu, ki ga sestavlja enakostranični trikotnik = 120°.

• vektorja a in c

Rep a in c sovpadata

Pri vektorjih a in c sovpadata repa obeh vektorjev, zato je kot med vektorjema a in c enak kotu med dvema stranicama enakostraničnega trikotnika = 60°.

2. naloga: Poiščite kote med vektorji, če tvorijo enakokraki pravokotni trikotnik.

• a in b vektorja
• b in c vektorja
• vektorja a in c

rešitev:

• a in b vektorja

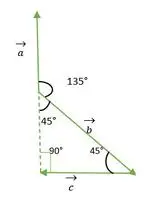
Pravokotni enakokraki trikotnik

celo število v niz v Javi

Iz zgornje slike vidimo, da glava ali rep vektorja a in b ne sovpadata drug z drugim. Torej z uporabo lastnosti - Vektor ostane nespremenjen, če se prenaša vzporedno s samim seboj.

vektor je premaknjen vzporedno sam s seboj

Zdaj repa vektorjev a in b sovpadata drug z drugim in tvorita kot, ki je enak zunanjemu kotu pravokotnega enakokrakega trikotnika = 135°.

• b in c vektorja

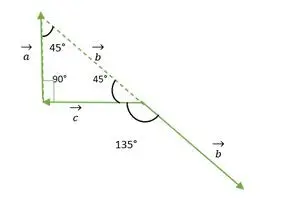
Pravokotni enakokraki trikotnik

Na zgornji sliki b in c vektorska glava ali rep ne sovpadata drug z drugim. Torej z uporabo lastnosti vektor ostane nespremenjen, če se prenaša vzporedno s samim seboj.

b vektor je premaknjen vzporedno sam s seboj

Zdaj repa vektorjev b in c sovpadata drug z drugim in tvorita kot, ki je enak zunanjemu kotu pravokotnega enakokrakega trikotnika = 135°.

css seznami

• vektorja a in c

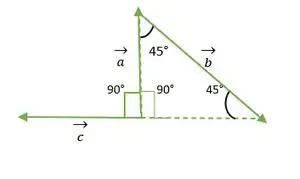
Pravokotni enakokraki trikotnik

Iz zgornje slike se vidi, da glava ali rep vektorja a in c ne sovpadata drug z drugim. Torej z uporabo lastnosti - Vektor ostane nespremenjen, če se prenaša vzporedno s samim seboj.

c vektor premakne vzporedno sam s seboj

Zdaj repa vektorjev a in c sovpadata drug z drugim in tvorita kot, ki je enak pravemu kotu enakokrakega trikotnika = 90°.

Naloga 3: Poiščite kot med vektorjema A = i + j + k in vektorjem B = -2i – 2j – 2k.

rešitev:

Iz formule,

A = A_xi + A_inj + A_zk

B= B_xi + B_inj + B_zk

cosθ=frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Tukaj v danem vprašanju,

A= i + j + k

B= -2i -2j -2k

Zamenjava vrednosti v formuli

⇒ cosθ =frac{(1.(-2)+1.(-2)+1.(-2))}{(sqrt{1^2+1^2+1^2}×sqrt{(-2)^2+(-2)^2+(-2)^2})}

⇒ cosθ =frac{(-2-2-2)}{(sqrt{1+1+1}×sqrt{4+4+4})}

⇒ cosθ =frac{-6}{(sqrt{3}×sqrt{12})}

⇒ cosθ =frac{-6}{(sqrt{36})}

⇒ cosθ = -6/6

⇒ cosθ= -1

⇒ θ = 180°

Naloga 4: Poiščite kot med vektorjem A = 3i + 4j in B = 2i + j

rešitev:

A = A_xi + A_inj + A_zk

B = B_xi + B_inj + B_zk

cosθ =frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Tukaj podano,

A = 3i + 4j + 0k

B= 2i + j + 0k

Zamenjava vrednosti v formuli,

⇒ cosθ =frac{(3.2+4.1+0.0)}{(sqrt{3^2+4^2+0^2}×sqrt{2^2+1^2+0^2})}

⇒ cosθ =frac{(6+4+0)}{(sqrt{9+16+0}×sqrt{4+1+0})}

⇒ cosθ =frac{(10)}{(sqrt{25}×sqrt{5})}

⇒ cosθ =frac{(10)}{(sqrt{125})}

⇒ θ = cos^-1(frac{(10)}{5.(sqrt{5})})

⇒ θ = cos^-1(frac{2}{(sqrt{5})})

Naloga 5: Poiščite kot med vektorjem A = i + j in vektorjem B = j + k.

rešitev:

Iz formule,

algoritem za rsa

A = A_xi + A_inj + A_zk

B = B_xi + B_inj + B_zk

cosθ =frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}

Tukaj v danem vprašanju,

⇒ A = i + j

⇒ B = j + k

⇒ cosθ =frac{(1.0+1.1+0.1)}{(sqrt{1^2+1^2+0^2}×sqrt{0^2+1^2+1^2})}

⇒ cosθ =frac{(1)}{(sqrt{1+1+0}×sqrt{0+1+1})}

⇒ cosθ =frac{1}{(sqrt{2}×sqrt{2})}

⇒ θ = cos^-1(1/2)

⇒ θ = 60°