2D niz lahko definiramo kot niz nizov. 2D niz je organiziran kot matrike, ki jih je mogoče predstaviti kot zbirko vrstic in stolpcev.
Vendar so 2D nizi ustvarjeni za implementacijo podatkovne strukture, ki je podobna relacijski bazi podatkov. Zagotavlja preprosto shranjevanje množice podatkov hkrati, ki jih je mogoče posredovati poljubnemu številu funkcij, kjer koli je to potrebno.
Kako deklarirati 2D Array
Sintaksa deklaracije dvodimenzionalne matrike je zelo podobna sintaksi enodimenzionalne matrike, ki je podana na naslednji način.
mylivecricket
int arr[max_rows][max_columns];
vendar ustvari podatkovno strukturo, ki je videti takole.
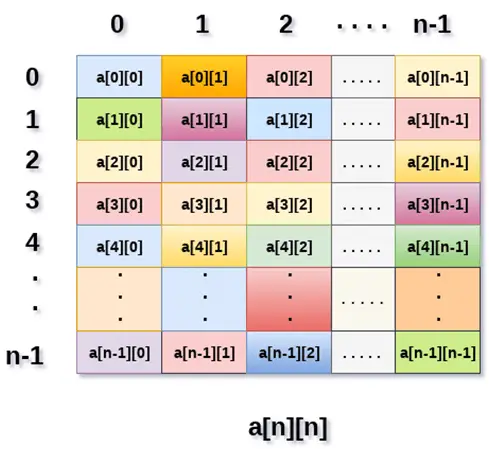
Zgornja slika prikazuje dvodimenzionalni niz, elementi so organizirani v obliki vrstic in stolpcev. Prvi element prve vrstice je predstavljen z [0][0], kjer je številka, prikazana v prvem indeksu, številka te vrstice, medtem ko je številka, prikazana v drugem indeksu, številka stolpca.
Kako dostopamo do podatkov v 2D nizu
Zaradi dejstva, da je do elementov 2D nizov mogoče naključno dostopati. Podobno kot pri enodimenzionalnih nizih lahko dostopamo do posameznih celic v 2D nizu z uporabo indeksov celic. Določeni celici sta pritrjena dva indeksa, eden je številka njene vrstice, drugi pa številka stolpca.
Vendar pa lahko vrednost, shranjeno v kateri koli določeni celici 2D polja, shranimo v neko spremenljivko x z uporabo naslednje sintakse.
int x = a[i][j];
kjer sta i in j številka vrstice oziroma stolpca celice.
ključ kandidata
Vsaki celici 2D polja lahko dodelimo 0 z uporabo naslednje kode:
for ( int i=0; i<n ;i++) { for (int j="0;" j<n; j++) a[i][j]="0;" } < pre> <h2>Initializing 2D Arrays </h2> <p>We know that, when we declare and initialize one dimensional array in C programming simultaneously, we don't need to specify the size of the array. However this will not work with 2D arrays. We will have to define at least the second dimension of the array. </p> <p>The syntax to declare and initialize the 2D array is given as follows. </p> <pre> int arr[2][2] = {0,1,2,3}; </pre> <p>The number of elements that can be present in a 2D array will always be equal to ( <strong>number of rows * number of columns</strong> ). </p> <p> <strong>Example :</strong> Storing User's data into a 2D array and printing it. </p> <p> <strong>C Example : </strong> </p> <pre> #include void main () { int arr[3][3],i,j; for (i=0;i<3;i++) { for (j="0;j<3;j++)" printf('enter a[%d][%d]: ',i,j); scanf('%d',&arr[i][j]); } printf('
printing the elements ....
'); for(i="0;i<3;i++)" printf('
'); printf('%d ',arr[i][j]); < pre> <h3>Java Example</h3> <pre> import java.util.Scanner; publicclass TwoDArray { publicstaticvoid main(String[] args) { int[][] arr = newint[3][3]; Scanner sc = new Scanner(System.in); for (inti =0;i<3;i++) { for(intj="0;j<3;j++)" system.out.print('enter element'); arr[i][j]="sc.nextInt();" system.out.println(); } system.out.println('printing elements...'); for(inti="0;i<3;i++)" system.out.print(arr[i][j]+' '); < pre> <h3>C# Example </h3> <pre> using System; public class Program { public static void Main() { int[,] arr = new int[3,3]; for (int i=0;i<3;i++) { for (int j="0;j<3;j++)" console.writeline('enter element'); arr[i,j]="Convert.ToInt32(Console.ReadLine());" } console.writeline('printing elements...'); i="0;i<3;i++)" console.writeline(); console.write(arr[i,j]+' '); < pre> <h2>Mapping 2D array to 1D array </h2> <p>When it comes to map a 2 dimensional array, most of us might think that why this mapping is required. However, 2 D arrays exists from the user point of view. 2D arrays are created to implement a relational database table lookalike data structure, in computer memory, the storage technique for 2D array is similar to that of an one dimensional array. </p> <p>The size of a two dimensional array is equal to the multiplication of number of rows and the number of columns present in the array. We do need to map two dimensional array to the one dimensional array in order to store them in the memory.</p> <p>A 3 X 3 two dimensional array is shown in the following image. However, this array needs to be mapped to a one dimensional array in order to store it into the memory. </p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-2.webp" alt="DS 2D Array"> <br> <p>There are two main techniques of storing 2D array elements into memory </p> <h3>1. Row Major ordering </h3> <p>In row major ordering, all the rows of the 2D array are stored into the memory contiguously. Considering the array shown in the above image, its memory allocation according to row major order is shown as follows. </p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-3.webp" alt="DS 2D Array"> <br> <p>first, the 1<sup>st</sup> row of the array is stored into the memory completely, then the 2<sup>nd</sup> row of the array is stored into the memory completely and so on till the last row.</p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-4.webp" alt="DS 2D Array"> <br> <h3>2. Column Major ordering </h3> <p>According to the column major ordering, all the columns of the 2D array are stored into the memory contiguously. The memory allocation of the array which is shown in in the above image is given as follows.</p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-5.webp" alt="DS 2D Array"> <br> <p>first, the 1<sup>st</sup> column of the array is stored into the memory completely, then the 2<sup>nd</sup> row of the array is stored into the memory completely and so on till the last column of the array. </p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-6.webp" alt="DS 2D Array"> <br> <h2>Calculating the Address of the random element of a 2D array </h2> <p>Due to the fact that, there are two different techniques of storing the two dimensional array into the memory, there are two different formulas to calculate the address of a random element of the 2D array. </p> <h3>By Row Major Order </h3> <p>If array is declared by a[m][n] where m is the number of rows while n is the number of columns, then address of an element a[i][j] of the array stored in row major order is calculated as, </p> <pre> Address(a[i][j]) = B. A. + (i * n + j) * size </pre> <p>where, B. A. is the base address or the address of the first element of the array a[0][0] . </p> <p> <strong>Example : </strong> </p> <pre> a[10...30, 55...75], base address of the array (BA) = 0, size of an element = 4 bytes . Find the location of a[15][68]. Address(a[15][68]) = 0 + ((15 - 10) x (68 - 55 + 1) + (68 - 55)) x 4 = (5 x 14 + 13) x 4 = 83 x 4 = 332 answer </pre> <h3>By Column major order </h3> <p>If array is declared by a[m][n] where m is the number of rows while n is the number of columns, then address of an element a[i][j] of the array stored in row major order is calculated as, </p> <pre> Address(a[i][j]) = ((j*m)+i)*Size + BA </pre> <p>where BA is the base address of the array. </p> <p> <strong>Example:</strong> </p> <pre> A [-5 ... +20][20 ... 70], BA = 1020, Size of element = 8 bytes. Find the location of a[0][30]. Address [A[0][30]) = ((30-20) x 24 + 5) x 8 + 1020 = 245 x 8 + 1020 = 2980 bytes </pre> <hr></3;i++)></pre></3;i++)></pre></3;i++)></pre></n> Število elementov, ki so lahko prisotni v 2D nizu, bo vedno enako ( število vrstic * število stolpcev ).
primer: Shranjevanje uporabnikovih podatkov v 2D polje in njihovo tiskanje.
C Primer:
#include void main () { int arr[3][3],i,j; for (i=0;i<3;i++) { for (j="0;j<3;j++)" printf(\'enter a[%d][%d]: \',i,j); scanf(\'%d\',&arr[i][j]); } printf(\'
printing the elements ....
\'); for(i="0;i<3;i++)" printf(\'
\'); printf(\'%d \',arr[i][j]); < pre> <h3>Java Example</h3> <pre> import java.util.Scanner; publicclass TwoDArray { publicstaticvoid main(String[] args) { int[][] arr = newint[3][3]; Scanner sc = new Scanner(System.in); for (inti =0;i<3;i++) { for(intj="0;j<3;j++)" system.out.print(\'enter element\'); arr[i][j]="sc.nextInt();" system.out.println(); } system.out.println(\'printing elements...\'); for(inti="0;i<3;i++)" system.out.print(arr[i][j]+\' \'); < pre> <h3>C# Example </h3> <pre> using System; public class Program { public static void Main() { int[,] arr = new int[3,3]; for (int i=0;i<3;i++) { for (int j="0;j<3;j++)" console.writeline(\'enter element\'); arr[i,j]="Convert.ToInt32(Console.ReadLine());" } console.writeline(\'printing elements...\'); i="0;i<3;i++)" console.writeline(); console.write(arr[i,j]+\' \'); < pre> <h2>Mapping 2D array to 1D array </h2> <p>When it comes to map a 2 dimensional array, most of us might think that why this mapping is required. However, 2 D arrays exists from the user point of view. 2D arrays are created to implement a relational database table lookalike data structure, in computer memory, the storage technique for 2D array is similar to that of an one dimensional array. </p> <p>The size of a two dimensional array is equal to the multiplication of number of rows and the number of columns present in the array. We do need to map two dimensional array to the one dimensional array in order to store them in the memory.</p> <p>A 3 X 3 two dimensional array is shown in the following image. However, this array needs to be mapped to a one dimensional array in order to store it into the memory. </p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-2.webp" alt="DS 2D Array"> <br> <p>There are two main techniques of storing 2D array elements into memory </p> <h3>1. Row Major ordering </h3> <p>In row major ordering, all the rows of the 2D array are stored into the memory contiguously. Considering the array shown in the above image, its memory allocation according to row major order is shown as follows. </p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-3.webp" alt="DS 2D Array"> <br> <p>first, the 1<sup>st</sup> row of the array is stored into the memory completely, then the 2<sup>nd</sup> row of the array is stored into the memory completely and so on till the last row.</p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-4.webp" alt="DS 2D Array"> <br> <h3>2. Column Major ordering </h3> <p>According to the column major ordering, all the columns of the 2D array are stored into the memory contiguously. The memory allocation of the array which is shown in in the above image is given as follows.</p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-5.webp" alt="DS 2D Array"> <br> <p>first, the 1<sup>st</sup> column of the array is stored into the memory completely, then the 2<sup>nd</sup> row of the array is stored into the memory completely and so on till the last column of the array. </p> <br> <img src="//techcodeview.com/img/ds-tutorial/80/2d-array-6.webp" alt="DS 2D Array"> <br> <h2>Calculating the Address of the random element of a 2D array </h2> <p>Due to the fact that, there are two different techniques of storing the two dimensional array into the memory, there are two different formulas to calculate the address of a random element of the 2D array. </p> <h3>By Row Major Order </h3> <p>If array is declared by a[m][n] where m is the number of rows while n is the number of columns, then address of an element a[i][j] of the array stored in row major order is calculated as, </p> <pre> Address(a[i][j]) = B. A. + (i * n + j) * size </pre> <p>where, B. A. is the base address or the address of the first element of the array a[0][0] . </p> <p> <strong>Example : </strong> </p> <pre> a[10...30, 55...75], base address of the array (BA) = 0, size of an element = 4 bytes . Find the location of a[15][68]. Address(a[15][68]) = 0 + ((15 - 10) x (68 - 55 + 1) + (68 - 55)) x 4 = (5 x 14 + 13) x 4 = 83 x 4 = 332 answer </pre> <h3>By Column major order </h3> <p>If array is declared by a[m][n] where m is the number of rows while n is the number of columns, then address of an element a[i][j] of the array stored in row major order is calculated as, </p> <pre> Address(a[i][j]) = ((j*m)+i)*Size + BA </pre> <p>where BA is the base address of the array. </p> <p> <strong>Example:</strong> </p> <pre> A [-5 ... +20][20 ... 70], BA = 1020, Size of element = 8 bytes. Find the location of a[0][30]. Address [A[0][30]) = ((30-20) x 24 + 5) x 8 + 1020 = 245 x 8 + 1020 = 2980 bytes </pre> <hr></3;i++)></pre></3;i++)></pre></3;i++)> kjer je B. A. osnovni naslov ali naslov prvega elementa matrike a[0][0] .
primer:
kaj pomeni xdxd
a[10...30, 55...75], base address of the array (BA) = 0, size of an element = 4 bytes . Find the location of a[15][68]. Address(a[15][68]) = 0 + ((15 - 10) x (68 - 55 + 1) + (68 - 55)) x 4 = (5 x 14 + 13) x 4 = 83 x 4 = 332 answer
Po glavnem naročilu v stolpcu
Če je matrika deklarirana z a[m][n], kjer je m število vrstic, medtem ko je n število stolpcev, potem se naslov elementa a[i][j] matrike, shranjene v glavnem vrstnem redu vrstice, izračuna kot ,
Address(a[i][j]) = ((j*m)+i)*Size + BA
kjer je BA osnovni naslov polja.
primer:
A [-5 ... +20][20 ... 70], BA = 1020, Size of element = 8 bytes. Find the location of a[0][30]. Address [A[0][30]) = ((30-20) x 24 + 5) x 8 + 1020 = 245 x 8 + 1020 = 2980 bytes
