Z-REZULTAT V STATISTIKI - PODATKOVNA ZNANOST

Z-rezultat v statistiki je meritev, koliko standardnih odstopanj ima podatkovna točka od povprečja porazdelitve. Poiščimo rezultat z v statistiki. Z-rezultat 0 pomeni, da je rezultat podatkovne točke enak povprečnemu rezultatu. Pozitivna z-rezultat pomeni, da je podatkovna točka nadpovprečna, medtem ko negativna z-rezultat pomeni, da je podatkovna točka podpovprečna.

Formula za izračun z-rezultata je: z = (x – μ)/ str

Kje:

x: je testna vrednost
m: je povprečje
pri: je standardna vrednost

V tem članku bomo razpravljali o naslednjih pojmih:

Kazalo

Kaj je Z-Score?
Kako izračunati Z-rezultat?
Značilnosti Z-Score
Izračunajte odstopanja z uporabo Z-vrednosti
Implementacija Z-Score v Pythonu
Uporaba Z-Score
Z-rezultati v primerjavi s standardnim odklonom
Zakaj se Z-rezultati imenujejo standardni rezultati?

Kaj je Z-Score?

Z-rezultat, znan tudi kot standardni rezultat, nam pove odstopanje podatkovne točke od povprečja, tako da ga izrazimo v smislu standardnih odklonov nad ali pod povprečjem. Da nam predstavo o tem, kako daleč je podatkovna točka od povprečja. Zato se Z-rezultat meri v smislu standardnega odklona od povprečja. Na primer, Z-rezultat 2 pomeni, da je vrednost 2 standardni odkloni oddaljena od povprečja. Za uporabo z-vrednosti moramo poznati populacijsko povprečje (μ) in tudi populacijski standardni odklon (σ).

Formula za Z-rezultat

Z-rezultat je mogoče izračunati z naslednjo formulo.

z = (X – μ) / str

kje,

z = Z-rezultat
X = vrednost elementa
μ = povprečje prebivalstva
σ = standardni odklon populacije

Kako izračunati Z-rezultat?

Podano nam je povprečje populacije (μ), standardno odstopanje populacije (σ) in opazovana vrednost (x) v izjavi o problemu, ki jo zamenjamo v enačbi Z-ocene, nam da vrednost Z-ocene. Odvisno od tega, ali je dani Z-Score pozitiven ali negativen, lahko uporabimo pozitivna Z-tabela oz negativna Z-tabela na voljo na spletu ali na zadnji strani vašega učbenika o statistiki v dodatku.

Primer 1:

Opravite izpit GATE in dosežete 500. Povprečna ocena za GATE je 390, standardna deviacija pa 45. Kako dobro ste dosegli rezultat na testu v primerjavi s povprečnim udeležencem testa?

css krepko

rešitev:

Naslednji podatki so na voljo v zgornjem vprašanju

Neobdelani rezultat/opazovana vrednost = X = 500

Povprečna ocena = μ = 390

Standardni odklon = σ = 45

Z uporabo formule z-score,

z = (X – μ) / str

z = (500 – 390) / 45

z = 110 / 45 = 2,44

To pomeni, da je vaš rezultat z 2.44 .

Ker je Z-rezultat pozitiven 2,44, bomo uporabili pozitivno Z-tabelo.

Zdaj pa si poglejmo Tabela Z (CC-BY), da bi vedeli, kako dober rezultat ste dosegli v primerjavi z drugimi preizkuševalci.

Sledite spodnjim navodilom, da poiščete verjetnost iz tabele.

tukaj, z-rezultat = 2,44, ki jaz označuje, da je podatkovna točka 2,44 standardne deviacije nad povprečjem.

Najprej preslikajte prvi dve števki 2.4 na os Y.
Nato vzdolž osi X zemljevid 0,04
Spojite obe osi. Presečišče obeh vam bo zagotovilo kumulativno verjetnost, povezano z vrednostjo Z-ocene, ki jo iščete

[Ta verjetnost predstavlja območje pod standardno normalno krivuljo levo od Z-vrednosti]

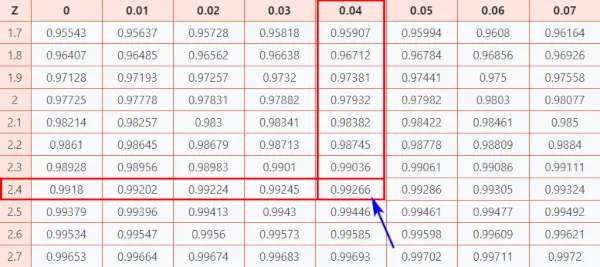
Normalna distribucijska tabela

Kot rezultat boste dobili končno vrednost, ki je 0,99266 .

Zdaj moramo primerjati naš prvotni rezultat 500 na izpitu GATE v primerjavi s povprečnim rezultatom serije. Da bi to naredili, moramo pretvoriti kumulativno verjetnost, povezano z Z-rezultatom, v odstotno vrednost.

0,99266 × 100 = 99,266 %

Končno lahko rečete, da ste se izkazali dobro kot skoraj 99% drugih testirancev.

Primer 2 : Kakšna je verjetnost, da študent doseže rezultate med 350 in 400 (s povprečno oceno μ 390 in standardnim odklonom σ 45)?

rešitev:

Min rezultat = X₁= 350

Največji rezultat = X₂= 400

Z uporabo formule z-score,

z₁= (X1 – m) / str

z₁= (350 – 390) / 45

z₁= -40 / 45 = -0,88
onclick javascript

z₂= (X₂– m) / str

z2 = (400 – 390) / 45

z₂= 10 / 45 = 0,22

Ker je z1 negativen, bomo morali pogledati negativ Z-tabela in ugotovimo, da je kumulativna verjetnost p1, prva verjetnost 0,18943 .

z₂je pozitiven, zato uporabimo pozitivno Z-tabelo, ki daje kumulativno verjetnost p₂od 0,58706 .

Končna verjetnost se izračuna z odštevanjem p1 od p₂:

p = str₂– str₁

p = 0,58706 – 0,18943 = 0,39763

Verjetnost, da študent doseže med 350 in 400, je 39,763 % (0,39763 * 100).
niz in podniz

Značilnosti Z-Score

Velikost Z-rezultata odraža, kako daleč je podatkovna točka od povprečja v smislu standardnih odstopanj.
Element, ki ima z-rezultat manj kot 0, pomeni, da je element nižji od povprečja.
Z-rezultati omogočajo primerjavo podatkovnih točk iz različnih porazdelitev.
Element, ki ima z-rezultat večji od 0, pomeni, da je element večji od povprečja.
Element, ki ima z-rezultat enako 0, pomeni, da je element enak povprečju.
Element, ki ima z-rezultat enak 1, pomeni, da je element za 1 standardni odklon večji od povprečja; z-vrednost, ki je enaka 2, 2 standardnima odklonoma večja od povprečja itd.
Element, ki ima z-rezultat enak -1, pomeni, da je element za 1 standardni odklon manjši od povprečja; z-vrednost, ki je enaka -2, 2 standardni deviaciji manj od povprečja itd.
Če je število elementov v danem nizu veliko, ima približno 68 % elementov z-rezultat med -1 in 1; približno 95 % jih ima z-rezultat med -2 in 2; približno 99 % ima z-rezultat med -3 in 3. To je znano kot empirično pravilo in navaja odstotek podatkov znotraj določenih standardnih odstopanj od povprečja v normalni porazdelitvi, kot je prikazano na spodnji sliki

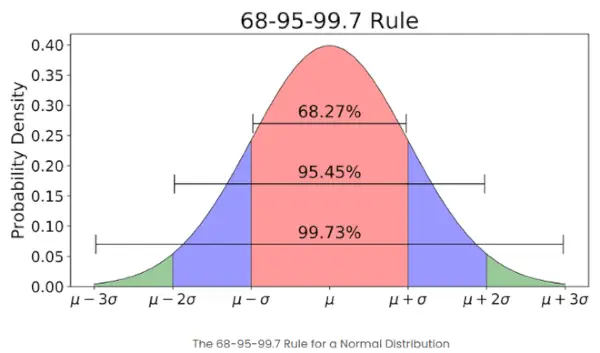
Empirično pravilo v normalni porazdelitvi

Izračunajte odstopanja z uporabo Z-vrednosti

V podatkih lahko izračunamo odstopanja z uporabo vrednosti z-rezultata podatkovnih točk. Koraki za upoštevanje izstopajoče podatkovne točke so naslednji:

Najprej zberemo nabor podatkov, v katerem želimo videti odstopanja
Izračunali bomo povprečje in standardni odklon nabora podatkov. Te vrednosti bodo uporabljene za izračun vrednosti z-rezultata vsake podatkovne točke.
Izračunali bomo vrednost z-rezultata za vsako podatkovno točko. Formula za izračun vrednosti z-score bo enaka kot
Z = frac{{X – mu}}{{sigma}}
kjer bo X podatkovna točka, μ povprečje podatkov in σ standardni odklon nabora podatkov.
Določili bomo mejno vrednost za z-rezultat, po kateri bi podatkovno točko lahko obravnavali kot izstopajočo vrednost. Ta mejna vrednost je hiperparameter, ki ga določimo glede na naš projekt.
Podatkovna točka, katere vrednost z-score je večja od 3, pomeni, da podatkovna točka ne pripada 99,73 % točki nabora podatkov.
Vsaka podatkovna točka, katere z-rezultat je večji od naše izbrane mejne vrednosti, bo obravnavana kot izstopajoča.

Preverite: Rezultat Z za zaznavanje odstopanj

Implementacija Z-Score v Pythonu

Python lahko uporabimo za izračun vrednosti z-score podatkovnih točk v naboru podatkov. Prav tako bomo uporabili knjižnico numpy za izračun povprečja in standardnega odklona nabora podatkov.

Python3

 import numpy as np def calculate_z_score(data): # Mean of the dataset mean = np.mean(data) # Standard Deviation of tha dataset std_dev = np.std(data) # Z-score of tha data points z_scores = (data - mean) / std_dev return z_scores # Example dataset dataset = [3,9, 23, 43,53, 4, 5,30, 35, 50, 70, 150, 6, 7, 8, 9, 10] z_scores = calculate_z_score(dataset) print('Z-Score :',z_scores) # Data points which lies outside 3 standard deviatioms are outliers # i.e outside range of99.73% values outliers = [data_point for data_point,  z_score in zip(dataset, z_scores) if z_score>3] print(f'
Osutniki v naboru podatkov so {outliers}')>

Izhod:

Z-rezultat: [-0,7574907 -0,59097335 -0,20243286 0,35262498 0,6301539 -0,72973781
-0,70198492 -0,00816262 0,13060185 0,54689523 1,10195307 3,32218443
-0,67423202 -0,64647913 -0,61872624 -0,59097335 -0,56322046]
Izstopajoči podatki v naboru podatkov so [150]

Uporaba Z-Score

Z-rezultati se pogosto uporabljajo za skaliranje funkcij, da se različne funkcije združijo v skupno lestvico. Funkcije za normalizacijo zagotavljajo, da imajo ničelno povprečje in varianco enote, kar je lahko koristno za nekatere algoritme strojnega učenja, zlasti tiste, ki se opirajo na mere razdalje.
Z-rezultate je mogoče uporabiti za prepoznavanje izstopajočih vrednosti v naboru podatkov. Podatkovne točke z Z-rezultati nad določenim pragom (običajno 3 standardne deviacije od povprečja) se lahko štejejo za izstopajoče.
Z-rezultate je mogoče uporabiti v algoritmih za odkrivanje nepravilnosti za prepoznavanje primerov, ki znatno odstopajo od pričakovanega vedenja.
Z-rezultate je mogoče uporabiti za pretvorbo poševnih porazdelitev v bolj normalne porazdelitve.
Pri delu z regresijskimi modeli je mogoče analizirati Z-rezultate ostankov, da preverimo homoskedastičnost (konstantno varianco ostankov).
Z-rezultate je mogoče uporabiti pri skaliranju značilnosti tako, da pogledamo njihova standardna odstopanja od povprečja.

Z-rezultati v primerjavi s standardnim odklonom

Z- rezultat	Standardni odklon
Pretvorite neobdelane podatke v standardizirano lestvico.	Meri količino variacije ali disperzije v nizu vrednosti.
Omogoča lažjo primerjavo vrednosti iz različnih naborov podatkov, ker odvzamejo izvirne merske enote.	Standardni odklon ohranja izvirne merske enote, zaradi česar je manj primeren za neposredne primerjave med nizi podatkov z različnimi enotami.
Navedite, kako daleč je podatkovna točka od povprečja v smislu standardnih odstopanj, kar zagotavlja merilo relativnega položaja podatkovne točke znotraj porazdelitve	Izraženo v istih enotah kot izvirni podatki, kar zagotavlja absolutno merilo, kako razpršene so vrednosti okoli povprečja

Preverite: Z-točkovna tabela

Zakaj se Z-rezultati imenujejo standardni rezultati?

Z-rezultati so znani tudi kot standardni rezultati, ker standardizirajo vrednost naključne spremenljivke. To pomeni, da ima seznam standardiziranih rezultatov povprečje 0 in standardno odstopanje 1,0. Z-rezultati omogočajo tudi primerjavo rezultatov različnih vrst spremenljivk. To je zato, ker uporabljajo relativni položaj za enačenje rezultatov različnih spremenljivk ali porazdelitev.

Z-rezultati se pogosto uporabljajo za primerjavo spremenljivke s standardno normalno porazdelitvijo (z μ = 0 in σ = 1).

Z-rezultat v statistiki – pogosta vprašanja

Kakšen je pomen pozitivnih in negativnih Z-rezultatov?

Pozitivni Z-rezultati označujejo vrednosti nad povprečjem, negativni Z-rezultati pa vrednosti pod povprečjem. Predznak odraža smer odstopanja od povprečja.

Kaj pomeni Z-rezultat 0?

Z-rezultat 0 pomeni, da je vrednost podatkovne točke točno na srednji vrednosti nabora podatkov. Nakazuje, da podatkovna točka ni niti nad niti pod povprečjem.

Kaj je pravilo 68-95-99,7 v zvezi z Z-rezultati?

Pravilo 68-95-99.7, znano tudi kot empirično pravilo, pravi, da:

Približno 68 % podatkov spada znotraj 1 standardnega odklona od povprečja.
Približno 95 % je znotraj 2 standardnih odstopanj.
Približno 99,7 % spada v 3 standardne deviacije.

Ali je mogoče Z-rezultate uporabiti za nenormalne porazdelitve?

Z-rezultati temeljijo na predpostavki, da podatki sledijo normalni porazdelitvi. Vendar so v praksi Z-rezultati koristni za podatke, ki sledijo normalni porazdelitvi. Medtem ko je Z-rezultate mogoče izračunati za katero koli distribucijo, njihova interpretacija postane manj zanesljiva in enostavna, če imamo opravka z neobičajno porazdeljenimi podatki.

Kako lahko Z-Scores uporabimo v resničnih situacijah?

Z-Scores imajo različne aplikacije, na primer v financah za analizo portfelja, izobraževanju za standardizirano testiranje, zdravstvu za klinične ocene itd. Zagotavljajo standardizirano merilo za primerjavo in razlago podatkov.