V tem članku bomo obravnavali prečkanje drevesa v podatkovni strukturi. Izraz 'prehod drevesa' pomeni prečkanje ali obisk vsakega vozlišča drevesa. Obstaja en sam način za prečkanje linearne podatkovne strukture, kot so povezani seznam, čakalna vrsta in sklad. Medtem ko obstaja več načinov za prečkanje drevesa, ki so navedeni kot sledi -
- Prehod po prednaročilu
- Prehod po vrstnem redu
- Prehod poštnega naloga
Torej, v tem članku bomo razpravljali o zgoraj naštetih tehnikah prečkanja drevesa. Zdaj pa začnimo razpravljati o načinih prečkanja drevesa.
Prehod po prednaročilu
Ta tehnika sledi politiki 'root left right'. To pomeni, da se obišče prvo korensko vozlišče, nato se rekurzivno prečka levo poddrevo in nazadnje rekurzivno prečka desno poddrevo. Ker je korensko vozlišče prečkano pred (ali pred) levim in desnim poddrevesom, se to imenuje prehod pred naročilom.
Torej je v prehodu pred naročilom vsako vozlišče obiskano pred obema poddrevesoma.
Aplikacije prečkanja prednaročila vključujejo -
- Uporablja se za ustvarjanje kopije drevesa.
- Uporablja se lahko tudi za pridobivanje predponskega izraza izraznega drevesa.
Algoritem
Until all nodes of the tree are not visited Step 1 - Visit the root node Step 2 - Traverse the left subtree recursively. Step 3 - Traverse the right subtree recursively.
Primer
Zdaj pa si oglejmo primer tehnike prečkanja prednaročila.
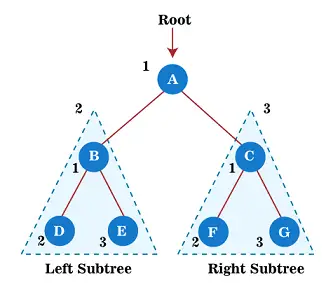
Zdaj začnite uporabljati prečkanje prednaročila na zgornjem drevesu. Najprej prečkamo korensko vozlišče A; nato se premaknite na njegovo levo poddrevo B , ki bo prav tako prehoden v prednaročilu.
Torej, za levo poddrevo B, najprej korensko vozlišče B se prečka sam; za tem levo poddrevo D je prehojeno. Od vozlišča D nima otrok, premakni se v desno poddrevo IN . Ker tudi vozlišče E nima otrok, je prečkanje levega poddrevesa korenskega vozlišča A končano.
kdaj se začne q2
Zdaj se pomaknite proti desnemu poddrevesu korenskega vozlišča A, ki je C. Torej, za desno poddrevo C, najprej korensko vozlišče C je prečkal samega sebe; za tem levo poddrevo F je prehojeno. Od vozlišča F nima otrok, premakni v desno poddrevo G . Ker tudi vozlišče G nima otrok, je prečkanje desnega poddrevesa korenskega vozlišča A zaključeno.
globalna var. v js
Zato so prečkana vsa vozlišča drevesa. Torej je rezultat prečkanja prednaročila zgornjega drevesa -
A → B → D → E → C → F → G
Če želite izvedeti več o prehodu prednaročila v strukturi podatkov, lahko sledite povezavi Prehod po prednaročilu .
Prehod poštnega naloga
Ta tehnika sledi politiki 'levo-desni koren'. To pomeni, da se prečka prvo levo poddrevo korenskega vozlišča, nato rekurzivno prečka desno poddrevo in na koncu prečka korensko vozlišče. Ker je korensko vozlišče prečkano za (ali po) levem in desnem poddrevesu, se to imenuje prehod po naročilu.
Torej je v prehodu po naročilu vsako vozlišče obiskano za obema poddrevesoma.
Aplikacije prečkanja po naročilu vključujejo -
- Uporablja se za brisanje drevesa.
- Uporablja se lahko tudi za pridobivanje postfiksnega izraza izraznega drevesa.
Algoritem
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Traverse the right subtree recursively. Step 3 - Visit the root node.
Primer
Zdaj pa si oglejmo primer tehnike prehoda po naročilu.

Zdaj začnite uporabljati prečkanje po naročilu na zgornjem drevesu. Najprej prečkamo levo poddrevo B, ki ga bomo prečkali po vrstnem redu. Nato bomo prečkali desno poddrevo C po naročilu. In končno, korensko vozlišče zgornjega drevesa, tj. A , se prečka.
Torej, za levo poddrevo B, najprej njegovo levo poddrevo D je prehojeno. Od vozlišča D nima otrok, prečkajte desno poddrevo IN . Ker tudi vozlišče E nima otrok, se pomaknite na korensko vozlišče B. Po prečkanju vozlišča B, prečkanje levega poddrevesa korenskega vozlišča A je končano.
Zdaj se pomaknite proti desnemu poddrevesu korenskega vozlišča A, ki je C. Torej, za desno poddrevo C, najprej njegovo levo poddrevo F je prehojeno. Od vozlišča F nima otrok, prečkajte desno poddrevo G . Ker tudi vozlišče G nima otrok, je končno korensko vozlišče desnega poddrevesa, tj. C, je prehojeno. Prehod desnega poddrevesa korenskega vozlišča A je končan.
Končno prečkajte korensko vozlišče danega drevesa, tj. A . Po prečkanju korenskega vozlišča je prečkanje po naročilu danega drevesa zaključeno.
Zato so prečkana vsa vozlišča drevesa. Torej je rezultat prehoda po naročilu zgornjega drevesa -
D → E → B → F → G → C → A
kako izbrati stolpce iz različnih tabel v sql
Če želite izvedeti več o prehodu po naročilu v podatkovni strukturi, lahko sledite povezavi Prehod poštnega naloga .
Prehod po vrstnem redu
Ta tehnika sledi politiki 'left root right'. To pomeni, da se po prehodu tega korenskega vozlišča obišče prvo levo poddrevo in na koncu še desno poddrevo. Ker je korensko vozlišče prečkano med levim in desnim poddrevesom, se imenuje prečkanje po vrstnem redu.
Torej je pri prehodu po vrstnem redu vsako vozlišče obiskano med njegovimi poddrevesi.
Aplikacije prečkanja Inorderja vključujejo -
- Uporablja se za pridobivanje vozlišč BST v naraščajočem vrstnem redu.
- Uporablja se lahko tudi za pridobivanje predponskega izraza izraznega drevesa.
Algoritem
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Visit the root node. Step 3 - Traverse the right subtree recursively.
Primer
Zdaj pa si oglejmo primer tehnike prečkanja Inorderja.

Zdaj začnite uporabljati prečkanje po vrstnem redu na zgornjem drevesu. Najprej prečkamo levo poddrevo B ki bodo prečkani po vrstnem redu. Po tem bomo prečkali korensko vozlišče A . In končno, desno poddrevo C se prečka v vrstnem redu.
Torej, za levo poddrevo B , najprej njegovo levo poddrevo D je prehoden. Od vozlišča D nima nobenih otrok, zato po njegovem prehodu vozlišče B bo prečkano in na koncu desno poddrevo vozlišča B, tj IN , se prečka. Vozlišče E tudi nima otrok; zato je prečkanje levega poddrevesa korenskega vozlišča A zaključeno.
java razvrščanje seznama
Nato prečkajte korensko vozlišče danega drevesa, tj. A .
Končno se premaknite proti desnemu poddrevesu korenskega vozlišča A, ki je C. Torej, za desno poddrevo C; najprej njegovo levo poddrevo F je prehojeno. Od vozlišča F nima otrok, vozl C bo prečkano in na koncu desno poddrevo vozlišča C, to je G , se prečka. Vozlišče G tudi nima otrok; zato je prečkanje desnega poddrevesa korenskega vozlišča A zaključeno.
Ko so prečkana vsa vozlišča drevesa, je prehod po vrstnem redu danega drevesa končan. Rezultat prečkanja zgornjega drevesa po vrstnem redu je -
D → B → E → A → F → C → G
Če želite izvedeti več o prehodu po vrstnem redu v strukturi podatkov, lahko sledite povezavi Prehod po vrstnem redu .
Kompleksnost tehnik prečkanja dreves
Časovna zapletenost zgoraj obravnavanih tehnik prečkanja dreves je O(n) , kje 'n' je velikost binarnega drevesa.
Medtem ko je zgoraj obravnavana prostorska kompleksnost tehnik prečkanja dreves O(1) če ne upoštevamo velikosti sklada za klice funkcij. Sicer pa je prostorska zahtevnost teh tehnik O(h) , kje 'h' je višina drevesa.
Izvedba prečkanja drevesa
Zdaj pa si oglejmo izvajanje zgoraj obravnavanih tehnik z uporabo različnih programskih jezikov.
Program: Napišite program za izvajanje tehnik prečkanja dreves v C.
spremenljivka globalni javascript
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(36); root->left = createNode(26); root->right = createNode(46); root->left->left = createNode(21); root->left->right = createNode(31); root->left->left->left = createNode(11); root->left->left->right = createNode(24); root->right->left = createNode(41); root->right->right = createNode(56); root->right->right->left = createNode(51); root->right->right->right = createNode(66); printf('
The Preorder traversal of given binary tree is -
'); traversePreorder(root); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); printf('
The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } Izhod

Program: Napišite program za izvajanje tehnik prečkanja drevesa v C#.
using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Preorder traversal of given binary tree is - '); bt.traversePreorder(); Console.WriteLine(); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); Console.WriteLine(); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } Izhod

Program: Napišite program za izvajanje tehnik prečkanja drevesa v C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout<<' '<element<left); traversepreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } *function to traverse the nodes of binary tree in postorder* void traversepostorder(struct node* root) { if (root="=" null) return; traversepostorder(root->left); traversePostorder(root->right); cout<<' '<element<left="createNode(28);" root->right = createNode(48); root->left->left = createNode(23); root->left->right = createNode(33); root->left->left->left = createNode(13); root->left->left->right = createNode(26); root->right->left = createNode(43); root->right->right = createNode(58); root->right->right->left = createNode(53); root->right->right->right = createNode(68); cout<<'
the preorder traversal of given binary tree is -
'; traversepreorder(root); cout<<'
inorder traverseinorder(root); postorder traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-6.webp" alt="Tree Traversal"> <p> <strong>Program:</strong> Write a program to implement tree traversal techniques in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class Tree { Node root; /* root of the tree */ Tree() { root = null; } /*function to print the nodes of given binary in Preorder*/ void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } /*function to print the nodes of given binary in Inorder*/ void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } /*function to print the nodes of given binary in Postorder*/ void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { Tree pt = new Tree(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println('
'); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println('
'); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-7.webp" alt="Tree Traversal"> <h2>Conclusion</h2> <p>In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.</p> <p>So, that's all about the article. Hope it will be helpful and informative to you.</p> <hr></'
></'></'></'> Izhod
Po izvedbi zgornje kode bo rezultat -

Zaključek
V tem članku smo razpravljali o različnih vrstah tehnik prečkanja drevesa: prečkanje pred vrstnim redom, prečkanje po vrstnem redu in prečkanje po vrstnem redu. Videli smo te tehnike skupaj z algoritmi, primeri, kompleksnostjo in implementacijo v C, C++, C# in Javi.
Torej, to je vse o članku. Upam, da vam bo koristno in informativno.
