The Časovna zapletenost of Merge Sort je O(n log n) v obeh povprečje in najhujši primeri . Kompleksnost prostora Spoji razvrsti je O(n) . 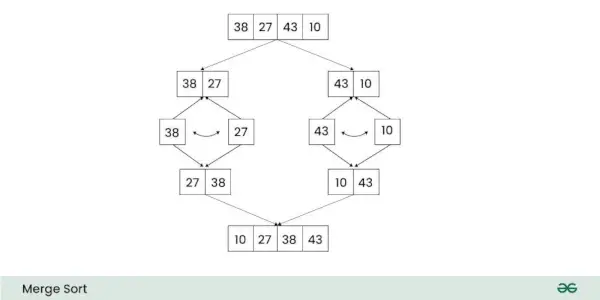
| Vidik | Kompleksnost |
|---|---|
| Časovna zapletenost | O(n log n) |
| Kompleksnost prostora | O(n) |
Analiza časovne zapletenosti razvrščanja z združevanjem:
Upoštevajte naslednjo terminologijo:
T(k) = čas, potreben za razvrščanje k elementov
M(k) = čas, potreben za spajanje k elementov
Torej, lahko se napiše
T(N) = 2 * T(N/2) + M(N)
= 2 * T(N/2) + konstanta * Nrazvrsti arraylist v javi
Ti elementi N/2 so nadalje razdeljeni na dve polovici. Torej,
T(N) = 2 * [2 * T(N/4) + konstanta * N/2] + konstanta * N
= 4 * T(N/4) + 2 * N * konstanta
. . .
= 2k* T(N/2k) + k * N * konstanta
Lahko se deli največ, dokler ne ostane en element. Torej, potem N/2k= 1. k = dnevnik 2 N
T(N) = N * T(1) + N * log2N * konstanta
= N + N * log2N
Zato je časovna kompleksnost O(N * log 2 N) .
Torej je v najboljšem, najslabšem in povprečnem primeru časovna kompleksnost enaka.
Analiza prostorske kompleksnosti razvrščanja z združitvijo:
Razvrščanje z združitvijo ima kompleksnost prostora od O(n) . To je zato, ker uporablja pomožni niz velikosti n da združite razvrščene polovice vhodne matrike. Pomožna matrika se uporablja za shranjevanje združenega rezultata, vhodna matrika pa je prepisana z razvrščenim rezultatom.
