Izmerite lahko tri dimenzije, dolžino, širino in višino, za vsak predmet, ki ga lahko vidite ali se ga dotaknete. Obstajajo določene dimenzije našega doma, v katerem živimo. Pravokotni zaslon/monitor, ki ga gledate, ima širino in širino svoje dolžine. Za vsako tridimenzionalno geometrijsko strukturo se meri površina in prostornina.
Zrak, ki ga pokriva površina predmeta, je površina katerega koli predmeta. Medtem ko je količina prostora, ki je na voljo v objektu, volumen.
Kazalo
- Površina
- Skupna površina
- Ukrivljena površina/stranska površina
- Glasnost
- Primeri površin in volumnov
- Pogosta vprašanja o formulah za površino in prostornino
Površina
Površino in prostornino je mogoče izračunati za katero koli tridimenzionalno (3D)geometrijsko obliko. Površina katerega koli območja je območje, ki ga zaseda površina predmeta. Prostornina je količina prostora, ki je na voljo v objektu. Imamo različne vrste oblik, kot so polobla, krogla, kocka, kvader, valj itd. Vse tridimenzionalne oblike imajo površino in prostornino. Toda dvodimenzionalne oblike, kot so kvadrati, pravokotniki, trikotniki, krogi itd.
Tukaj v dvodimenzionalnem merilu lahko merimo le površino. Območje, ki ga tridimenzionalni predmet zaseda z zunanjo površino, se imenuje površina. Meri se v kvadratnih enotah.
Območje je dveh vrst:
- Skupna površina
- Ukrivljena površina/stranska površina
Skupna površina
Površina, vključno z osnovo(-ami) in ukrivljenim delom, ustreza celotni površini. Je količina površine, ki jo obdaja površina predmeta. Če ima obrazec ukrivljeno osnovo in površino, bi bila vsota obeh regij skupna površina. Skupno površino lahko definiramo kot celotno površino, ki jo pokriva predmet, vključno z njegovo osnovo in ukrivljenim delom. Če ima predmet tako osnovno kot ukrivljeno površino, bo skupna površina enaka vsoti osnovne in ukrivljene površine.
- Skupna površina je skupna površina, ki jo zaseda predmet.
- Za primer vzemimo kvader, ki ima 6 ploskev, 12 robov in 8 oglišč.
Skupna površina = osnovna površina + ukrivljena površina
spomladanski oblak
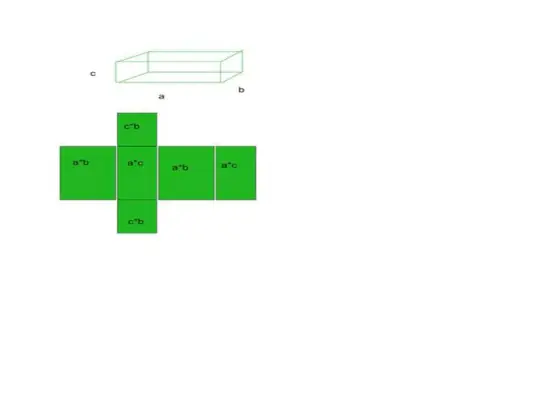
- Vsota vseh teh 6 površin bo naša skupna površina določene oblike
primer:
Spodaj je prikazan kvader, katerega dimenzija je dolžina = 8 cm, širina = 4 cm in višina = 6 cm, poiščite TSA kvadra
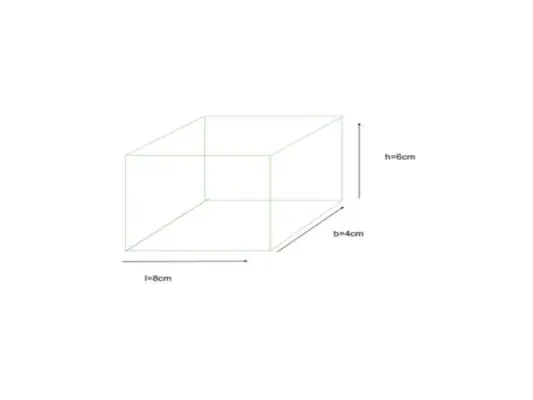
glede na l = 8 cm, b = 4 cm, h = 6 cm
TSA = 2((l * b) + (l * h) + (b * h))
= 2((8 * 4) + (8 * 6) + (4 * 6))
= 2((32) + (48) + (24))
= 2(104)
= 208
TSA kvadra je 208 cm.
Ukrivljena površina/stranska površina
Ukrivljena površina, razen središča, ustreza površini samo ukrivljenega dela oblike (oblik). Za oblike, kot je stožec, se pogosto imenuje stranska površina. Bočno površino lahko definiramo kot območje, ki vključuje le ukrivljeno površino predmeta ali stransko površino predmeta z izključitvijo osnovne površine predmeta. Območje stranske površine je znano tudi kot območje ukrivljene površine.
Večina oblik ali predmetov se nanaša na ukrivljeno površino, oblika ali predmetu podoben valj pa se nanaša na stransko površino. Preprosto povedano, območje, ki nam je vidno, se imenuje bočna površina. Na primer, razmislite o valju, kot je prikazano na spodnji sliki.
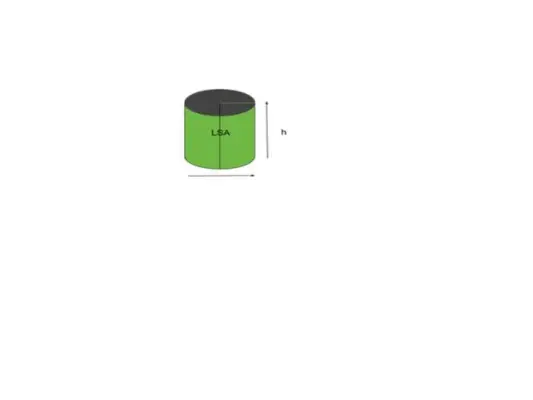
Glasnost
Volumen je količina prostora v določenem 3D objektu. Celotna količina prostora, ki ga predmet ali snov zaseda, se imenuje prostornina. Meri se v kubičnih enotah.
Formule za površino in prostornino
Podana tabela vsebuje skupno površino, ukrivljeno površino/stransko površino in prostornino različnih oblik.
| Ime oblike | Ukrivljena površina | Skupna površina | Glasnost |
|---|---|---|---|
| Kockast | 2h (l + b) | 2 (lb + bh + hl) | l * b * h |
| Kocka | 4a2 | 6a2 | a3 |
| Cilinder | 2πrh | 2π(r + h) | πr2h |
| krogla | 4πr2 moj kriket v živo | 4πr2 | 4/3π r3 |
| Stožec | πrl | πr(r + l) | 1/3π r2h |
| Hemisfera | 2pr2 | 3πr2 | 2/3π r3 |
Preberi več:
- Površina piramide
- Površina cilindra
- Površina hemisfere
- Površina krogle
- Površina kvadra
Primeri površin in volumnov
Primer 1: 2 kocki s prostornino 512 cm 3 so spojeni od konca do konca. Poiščite površino nastalega kvadra?
rešitev:
podano,
Prostornina (V) vsake kocke je = 512 cm3
zdaj lahko impliciramo, da a3= 512 cm3
∴ Stranica kocke, tj. a = 8 cm
Zdaj bosta širina in dolžina nastalega kvadra vsaka 8 cm, njegova višina pa 16 cm.
Torej, površina kvadra (TSA) = 2 (lb + bh + lh)
Zdaj, s postavitvijo vrednosti, dobimo,
= 2(8 × 16 + 8 × 8 + 16 × 8) cm 2
= (2 × 320) = 640 cm 2
Zato je TSA kvadra = 640 cm 2
Primer 2: Imamo valjasto svečo premera 14 cm in dolžine 2 cm. Stopi se tako, da nastane kvadrasta sveča dimenzij 7 cm × 11 cm × 1 cm. Koliko kuboidnih sveč je mogoče dobiti?
rešitev:
Mere cilindrične sveče:
Polmer valjaste sveče = 14/2 cm = 7 cm
Višina/debelina=2 cm
Prostornina ene cilindrične sveče = πr2h = π x 7 x 7 x (2) cm3= 308 cm3.
Prostornina kvadra sveča = 7 x 11 x 1 = 77 cm3
Zato je število kockastih sveč = prostornina kvadraste sveče/prostornina ene cilindrične sveče = 308/77 = 4
Tako lahko dobimo 4 sveče kockaste oblike.
Primer 3: Ženska želi iz gline sestaviti sferično kroglo, katere polmer je enak polmeru zapestnice, ki jo nosi. Glede na to, da je zapestnica okrogle oblike, želi tudi, da je površina zapestnice enaka volumnu krogle. Ugotovite polmer zapestnice, ki jo nosi?
rešitev:
Naj bo r polmer zapestnice in krogle,
Podano nam je, da je prostornina krogle enaka površini zapestnice:
torej
πr2= 4/3 πr3
⇒ r = 3/4
Zato je polmer zapestnice 3/4 enote.
Primer 4: Podano je, da je poševna višina pravilnega krožnega stožca 25 cm, njegova višina pa 24 cm. Poiščite ukrivljeno površino stožca?
rešitev:
Formula za ukrivljeno površino stožca je πrl. Kjer je r polmer stožca in l poševna višina stožca.
Tukaj je stožec desni krožni stožec.
Torej bi bil polmer stožca:
trikratna zimar= sqrt{l^2 – h^2}
=>r = sqrt{25^2 – 24^2}
=> r = 7 cm.
Zdaj izračunamo ukrivljeno površino:
Zahtevana površina = (22/7) * 7 * 25 = 550 cm2
Zato je ukrivljena površina stožca 550 cm 2 .
Primer 5: Poiščite stransko površino valja z osnovnim polmerom 6 palcev in višino 14 palcev.
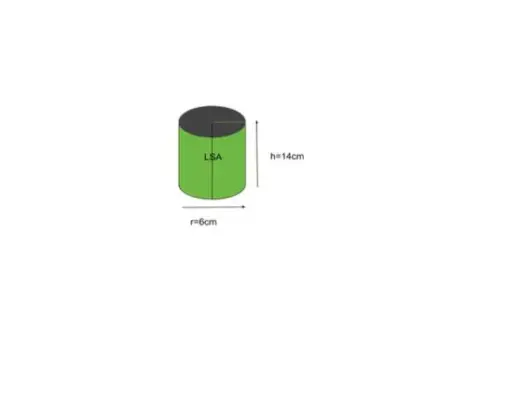
rešitev:
Podan polmer r = 6, višina h = 14
LSA = 2∏rh
= 2 * ∏ * 6 * 14
= 168∏
= 527.787
= 528.
LSA danega valja je 528 cm .
Vprašanje za vajo o površinah in volumnih
Različno Vprašanja za vadbo o površinah in volumnu formule so:
Q1. Poiščite površino kocke s stranico 5 centimetrov.
Q2. Izračunaj prostornino krogle s polmerom 3 metre.
Q3. Določite skupno površino valja s polmerom 4 centimetre in višino 8 centimetrov.
Q4. Poiščite prostornino stožca s polmerom 6 palcev in višino 10 palcev.
V5. Izračunajte površino pravokotne prizme z dolžino 7 metrov, širino 4 metre in višino 6 metrov.
Pogosta vprašanja o formulah za površino in prostornino
Kakšne so formule za površino in prostornino?
V zgornjem članku so dodane različne formule za površino in prostornino.
Kakšna je formula za površinsko prostornino razreda 10?
Formula za površinski in prostorninski razred 10 vsebuje:
| Ime oblike | Ukrivljena površina | Skupna površina | Glasnost |
|---|---|---|---|
| Kockast zakaj je niz nespremenljiv v Javi | 2h (l + b) | 2 (lb + bh + hl) | l × š × v |
| Kocka | 4a2 | 6a2 | a3 |
| Cilinder | 2πrh | 2π(r + h) | πr2h |
| krogla | 4πr2 | 4πr2 | 4/3π r3 |
| Stožec | πrl | πr(r + l) | 1/3π r2h |
| Hemisfera | 2pr2 | 3πr2 | 2/3π r3 |
Kakšna je formula kvadra v površini in prostornini?
- Površina kvadra = 2 (lb + bh + hl)
- Prostornina Cubiod = l × b × h
Kaj je površina in prostornina?
Površina je površina vseh površin trdne snovi, njena prostornina pa je prostor, ki ga zaseda snov.
