Kaj je seznam za preskok?
Preskočni seznam je verjetnostna podatkovna struktura. Preskočni seznam se uporablja za shranjevanje razvrščenega seznama elementov ali podatkov s povezanim seznamom. Omogoča učinkovit ogled procesa elementov ali podatkov. V enem samem koraku preskoči več elementov celotnega seznama, zato je znan kot preskočni seznam.
Preskočni seznam je razširjena različica povezanega seznama. Uporabniku omogoča zelo hitro iskanje, odstranjevanje in vstavljanje elementa. Sestavljen je iz osnovnega seznama, ki vključuje nabor elementov, ki ohranja hierarhijo povezav naslednjih elementov.
Struktura seznama preskokov
Zgrajen je v dveh slojih: najnižjem sloju in zgornjem sloju.
Najnižja plast preskočenega seznama je običajno razvrščen povezan seznam, zgornje plasti preskočenega seznama pa so kot 'hitra linija', kjer se elementi preskočijo.
Tabela kompleksnosti preskočnega seznama
| da ne | Kompleksnost | Povprečen primer | V najslabšem primeru |
|---|---|---|---|
| 1. | Kompleksnost dostopa | O (prijava) | O(n) |
| 2. | Kompleksnost iskanja | O (prijava) | O(n) |
| 3. | Izbriši kompleksnost | O (prijava) | O(n) |
| 4. | Kompleksnost vložka | O (prijava) | O(n) |
| 5. | Kompleksnost prostora | - | O(nlogn) |
Delovanje preskočnega seznama
Vzemimo primer, da bomo razumeli delovanje preskočenega seznama. V tem primeru imamo 14 vozlišč, tako da so ta vozlišča razdeljena na dve plasti, kot je prikazano na diagramu.
Spodnja plast je skupna linija, ki povezuje vsa vozlišča, zgornja plast pa je hitra linija, ki povezuje samo glavna vozlišča, kot lahko vidite na diagramu.
Recimo, da želite najti 47 v tem primeru. Iskanje boste začeli od prvega vozlišča hitre linije in nadaljevali s tekom po hitri liniji, dokler ne najdete vozlišča, ki je enako 47 ali več kot 47.
V primeru lahko vidite, da 47 ne obstaja v hitri liniji, zato iščete vozlišče manjše od 47, kar je 40. Zdaj greste na običajno linijo s pomočjo 40 in poiščete 47, kot je prikazano na diagramu.
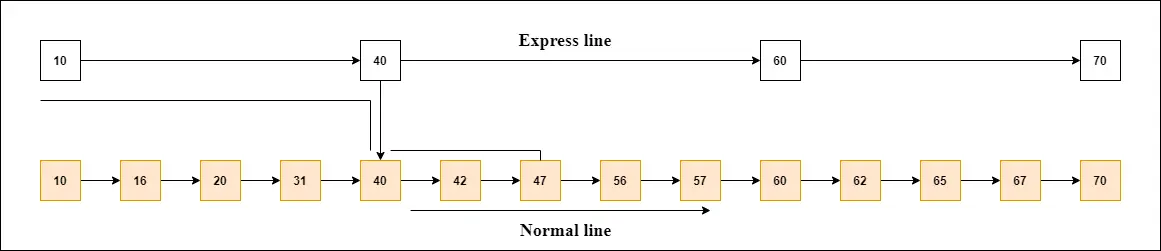
Opomba: Ko najdete takšno vozlišče na 'hitri liniji', greste s tega vozlišča na 'običajni pas' s kazalcem in ko iščete vozlišče v normalni liniji.
Preskoči seznam osnovnih operacij
Na preskočnem seznamu so naslednje vrste operacij.
Algoritem operacije vstavljanja
Insertion (L, Key) local update [0...Max_Level + 1] a = L → header for i = L → level down to 0 do. while a → forward[i] → key forward[i] update[i] = a a = a → forward[0] lvl = random_Level() if lvl > L → level then for i = L → level + 1 to lvl do update[i] = L → header L → level = lvl a = makeNode(lvl, Key, value) for i = 0 to level do a → forward[i] = update[i] → forward[i] update[i] → forward[i] = a
Algoritem operacije brisanja
Deletion (L, Key) local update [0... Max_Level + 1] a = L → header for i = L → level down to 0 do. while a → forward[i] → key forward[i] update[i] = a a = a → forward[0] if a → key = Key then for i = 0 to L → level do if update[i] → forward[i] ? a then break update[i] → forward[i] = a → forward[i] free(a) while L → level > 0 and L → header → forward[L → level] = NIL do L → level = L → level - 1
Algoritem iskalne operacije
Searching (L, SKey) a = L → header loop invariant: a → key level down to 0 do. while a → forward[i] → key forward[i] a = a → forward[0] if a → key = SKey then return a → value else return failure
Primer 1: Ustvarite preskočni seznam, v prazen preskočni seznam želimo vstaviti naslednje ključe.
- 6 s stopnjo 1.
- 29 s stopnjo 1.
- 22 s stopnjo 4.
- 9 s stopnjo 3.
- 17 s stopnjo 1.
- 4 z 2. stopnjo.
leta:
Korak 1: Vstavite 6 s stopnjo 1

2. korak: Vstavite 29 s stopnjo 1

3. korak: Vstavite 22 s stopnjo 4

4. korak: Vstavite 9 s stopnjo 3

5. korak: Vstavite 17 s stopnjo 1

6. korak: Vstavite 4 s stopnjo 2

Primer 2: Razmislite o tem primeru, kjer želimo iskati ključ 17.

leta:

Prednosti seznama Skip
- Če želite na preskočni seznam vstaviti novo vozlišče, bo vozlišče vstavljeno zelo hitro, ker na preskočnem seznamu ni rotacij.
- Preskočni seznam je preprost za implementacijo v primerjavi z zgoščeno tabelo in binarnim iskalnim drevesom.
- Na seznamu je zelo preprosto najti vozlišče, saj vozlišča shranjuje v razvrščeni obliki.
- Algoritem preskočenih seznamov je mogoče zelo enostavno spremeniti v bolj specifično strukturo, kot so indeksirani preskočni seznami, drevesa ali prednostne čakalne vrste.
- Preskočni seznam je robusten in zanesljiv seznam.
Slabosti seznama Skip
- Zahteva več pomnilnika kot uravnoteženo drevo.
- Povratno iskanje ni dovoljeno.
- Preskočni seznam išče vozlišče veliko počasneje kot povezani seznam.
Aplikacije seznama Skip
- Uporablja se v porazdeljenih aplikacijah in predstavlja kazalce in sistem v porazdeljenih aplikacijah.
- Uporablja se za implementacijo dinamične elastične sočasne čakalne vrste z nizko konkurenco pri zaklepanju.
- Uporablja se tudi z razredom predlog QMap.
- Indeksiranje preskočenega seznama se uporablja pri izvajanju težav z mediano.
- Preskočni seznam se uporablja za objavo delta kodiranja v iskanju Lucene.
