Formule Sin Cos v trigonometriji: Trigonometrija, kot pove že njeno ime, je preučevanje trikotnikov. Je pomembna veja matematike, ki preučuje razmerje med dolžinami stranic in koti pravokotnega trikotnika ter pomaga pri določanju manjkajočih dolžin stranic ali kotov trikotnika. Obstaja šest trigonometričnih razmerij ali funkcij: sinus, kosinus, tangens, kosekans, sekans in kotangens, kjer so kosekans, sekans in kotangens recipročne funkcije ostalih treh funkcij, tj. sinusa, kosinusa in tangensa.
Trigonometrično razmerje je definirano kot razmerje dolžin stranic pravokotnega trikotnika. Trigonometrija se v vsakdanjem življenju uporablja na različnih področjih. Pomaga pri določanju višine hribov ali zgradb. Uporablja se tudi na področjih, kot so kriminologija, gradbeništvo, fizika, arheologija, inženiring ladijskih motorjev itd.
V tem članku bomo raziskali vse trigonometrične formule večinoma sin in cos formule z njihovimi primeri ter seznam vseh formul v trigonometriji.
Kazalo
- Formule v trigonometriji
- Nekaj osnovnih formul Sin Cos
- Tabela formul Sin Cos
- Primeri formul Sin Cos
- Vadbene naloge s formulami Sin Cos v trigonometriji s primeri
Formule v trigonometriji
Oglejmo si pravokotni trikotnik XYZ, kjer je ∠Y = 90°. Naj bo kot pri točki Z enak θ. Stran, ki meji na θ, se imenuje sosednja stran, stran, ki je nasprotna θ, pa nasprotna stran. Hipotenuza je stranica, ki je nasprotna pravemu kotu, ali najdaljša stranica pravega kota.
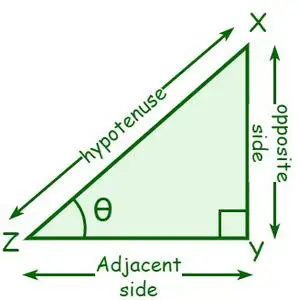
- sin θ = Nasprotna stranica/hipotenuza
- cos θ = sosednja stran/hipotenuza
- tan θ = nasprotna stran/sosednja stran
- cosec θ = 1/sin θ = hipotenuza/nasprotna stran
- sec θ = 1/ cos θ = hipotenuza/sosednja stranica
- posteljica θ = 1/tan θ = sosednja stran/nasprotna stran
Sinusna formula
Sinus kota v pravokotnem trikotniku je razmerje med dolžino nasprotne stranice in dolžino hipotenuze glede na dani kot. Sinusna funkcija je predstavljena kot sin.
sin θ = Nasprotna stranica/hipotenuza
Kosinusna formula
Kosinus kota v pravokotnem trikotniku je razmerje med dolžino sosednje stranice in dolžino hipotenuze glede na dani kot. Kosinusna funkcija je predstavljena kot cos.
seznam razvrščenih javacos θ = sosednja stran/hipotenuza
Nekaj osnovnih formul Sin Cos
Sinusne in kosinusne funkcije v kvadrantih
- Sinusna funkcija je pozitivna v prvem in drugem kvadrantu ter negativna v tretjem in četrtem kvadrantu.
- Kosinusna funkcija je pozitivna v prvem in četrtem kvadrantu ter negativna v drugem in tretjem kvadrantu.
Stopnje
Kvadrant
Znak sinusne funkcije
Predznak kosinusne funkcije
0° do 90°
1. kvadrant
+ (pozitivno)
+ (pozitivno)
90° do 180°
2. kvadrant
+ (pozitivno)
– (negativno)
180° do 270°
3. kvadrant
– (negativno)
– (negativno)
270° do 360°
4. kvadrant
– (negativno)
+ (pozitivno)
Identiteta negativnega kota funkcij sinusa in kosinusa
- Sinus negativnega kota je vedno enak negativnemu sinusu kota.
sin (– θ) = – sin θ
- Kosinus negativnega kota je vedno enak kosinusu kota.
cos (– θ) = cos θ
Razmerje med sinusno in kosinusno funkcijo
sin θ = cos (90° – θ)
Recipročne funkcije sinusne in kosinusne funkcije
- Kosekantna funkcija je recipročna funkcija sinusne funkcije.
cosec θ = 1/sin θ
- Funkcija sekanta je recipročna funkcija kosinusne funkcije.
sec θ = 1/cos θ
Pitagorejska identiteta
brez 2 θ + cos 2 θ = 1
Periodične identitete sinusne in kosinusne funkcije
sin (θ + 2nπ) = sin θ
cos (θ + 2nπ) = cos θ
Formule dvojnega kota za funkcije sinusa in kosinusa
sin 2θ = 2 sin θ cos θ
cos 2θ = cos 2 θ – greh 2 θ = 2 cos 2 θ – 1 = 1 – 2 sin 2 jaz
Identitete polovičnega kota za sinusno in kosinusno funkcijo
sin (θ/2) = ±√[(1 – cos θ)/2]
cos (θ/2) = ±√[(1 + cos θ)/2]
Identitete trojnega kota za sinusno in kosinusno funkcijo
sin 3θ = 3 sin θ – 4 sin 3 jaz
cos 3θ = 4cos 3 θ – 3 cos θ
Formule vsote in razlike
- Sinusna funkcija
sin (A + B) = sin A cos B + cos A sin B
sin (A – B) = sin A cos B – cos A sin B
- Kosinusna funkcija
cos (A + B) = cos A cos B – sin A sin B
cos (A – B) = cos A cos B + sin A sin B
Zakon sinusov ali sinusno pravilo
Pravilo sinusov sinusa je trigonometrični zakon, ki določa razmerje med dolžinami stranic in koti trikotnika.

a/sin A = b/sin B = c/sin C
Pri čemer so a, b in c dolžine treh stranic trikotnika ABC, A, B in C pa koti.
Zakon kosinusov
Pravilo kosinusa kosinusa se uporablja za določanje manjkajočih ali neznanih kotov ali dolžin stranic trikotnika.

a 2 = b 2 + c 2 – 2bc cos A
b 2 = c 2 + a 2 – 2ca cos B
c 2 = a 2 + b 2 – 2ab cos C
Pri čemer so a, b in c dolžine treh stranic trikotnika ABC, A, B in C pa koti.
Tabela formul Sin Cos
Tukaj je tabela/seznam formul Sin in Cos za različne kote v stopinjah in radianih:
Seznam formul Sin Cos
| Kot (v stopinjah) | Kot (v radianih) | greh i | cos θ |
|---|---|---|---|
| 0° | 0 | 0 | 1 |
| 30° | str/6 | 1/2 | _3/2 |
| 45° | str/4 | 1/√2 | 1/√2 |
| 60° | p/3 | √3/2 | 1/2 |
| 90° | p/2 | 1 | 0 |
| 120° | 2p/3 | √3/2 | -1/2 |
| 150° | 5p/6 | 1/2 | -√3/2 |
| 180° | Pi | 0 | -1 |
Primeri formul Sin Cos
Problem 1: Če je cos α = 24/25, potem poiščite vrednost sin α.
rešitev:
podano,
cos α = 24/25
Iz pitagorejskih identitet imamo;
cos2θ + sin2θ = 1
(24/25)2+ brez2α = 1
brez2α = 1 – (24/25)2
brez2α = 1 – (576/625) = (625 – 576)/625
brez2α = (625 – 576)/625 = 49/626
sin α = √49/625 = ±7/25
Zato je sin α = ±7/25.
Problem 2: Dokaži formuli za sin 2A in cos 2A, če je ∠A= 30°.
rešitev:
Podano je ∠A= 30°
Vemo, da
1) sin 2A = 2 sin A cos A
sin 2(30°) = 2 sin 30° cos 30°
sin 60° = 2 × (1/2) × (√3/2) {Ker je sin 30° = 1/2, cos 30° = √3/2 in sin 60° = √3/2}
√3/2 = √3/2
L.H.S = R.H.S
2) cos 2A = 2cos2A – 1
cos 2(30°) = 2cos2(30°) – 1
cos 60° = 2(√3/2)2– 1 = 3/2 – 1 {Ker je cos 60° = 1/2 in cos 30° = √3/2}
1/2 = 1/2
L.H.S = R.H.S
Zato dokazano.
Problem 3: Poiščite vrednost cos x, če je tan x = 3/4.
rešitev:
Podano, tan x = 3/4
Vemo, da
tan x = nasprotna stran/sosednja stran = 3/4
Za iskanje hipotenuze uporabimo Pitagorov izrek:
hipotenuza2= nasprotje2+ sosednji2
H2= 32+ 42
H2= 9 + 16 = 25
H = √25 = 5
Zdaj, cos x = sosednja stranica/hipotenuza
cos x = 4/5
Tako je vrednost cos x 4/5.
4. naloga: Poiščite ∠C (v stopinjah) in ∠A (v stopinjah), če je ∠B = 45°, BC = 15 in AC = 12 in.

rešitev:
Podano: ∠B = 45°, BC = a = 15 in AC = b = 12 in.
Iz zakona sinusov imamo
a/sin A = b/sin B = c/sin C
⇒ a/sin A = b/sin B
⇒ 15/sin A = 12/sin 45°
⇒ 15/sin A = 12/(1/√2)
⇒ 15/sin A = 12√2 = 16,97
⇒ brez A = 15/16,97 = 0,8839
⇒ ∠A = greh-1(0,8839) = 62,11°
Vemo, da je vsota notranjih kotov trikotnika 180°.
Torej, ∠A + ∠B + ∠C = 180°
⇒ 62,11° + 45° + ∠C = 180°
⇒ ∠C = 180° – (62,11° + 45°) = 72,89°
Zato je ∠A = 62,11° in ∠C = 72,89°.
Problem 5: Dokaži identitete polovičnega kota kosinusne funkcije.
rešitev:
Identiteta polovičnega kota kosinusne funkcije je:
cos (θ/2) = ±√[(1 + cos θ)/2]
Iz identitet z dvojnim kotom imamo,
cos 2A = 2 cos2A – 1
Zdaj zamenjajte A z θ/2 na obeh straneh
⇒ cos 2(θ/2) = 2 cos2(i/2) – 1
⇒ cos θ = 2 cos2(i/2) – 1
⇒ 2cos2(θ/2) = cos θ + 1
⇒ cos2(θ/2) = (cos θ + 1)/2
⇒ cos (θ/2) = ±√[(1 + cos θ)/2]
Zato dokazano.
Vadbene naloge s formulami Sin Cos v trigonometriji s primeri
1. Glede na sin θ = 3/5. Poiščite cos θ.
2. Dokažite istovetnost sin(2A) = 2 sinA cosA za A=45∘.
3. Če je cos α = 5/13. Poiščite greh (2a).
niz int
4. Rešite za θ, če je sin θ = cos(90∘−θ).
5. Če je tan β = 2. Poiščite sin β in cos β z uporabo pitagorejske identitete.
Pogosta vprašanja o formulah Sin Cos v trigonometriji s primeri
Katere so osnovne formule sinusa in kosinusa v trigonometriji?
Osnovni formuli za sinus in kosinus sta sin θ = Nasprotje/hipotenuza in cos θ = Sosednji/hipotenuza, kjer je θ kot v pravokotnem trikotniku.
Kako najdete sinus in kosinus posebnih kotov?
Posebni koti, kot so 0∘, 30∘, 45∘, 60∘ in 90∘, imajo specifične sinusne in kosinusne vrednosti, ki si jih je mogoče zapomniti s pomočjo trigonometričnih tabel ali konceptov enotskega kroga.
Kakšno je razmerje med funkcijama sinus in kosinus?
Funkciji sinus in kosinus sta povezani z identiteto sin θ = cos(90∘- θ) in pitagorejsko identiteto brez 2 θ+cos 2 θ = 1.
Kako uporabljate formule dvojnega kota za sinus in kosinus?
Formule dvojnega kota so sin(2θ) = 2sinθcosθ in cos(2θ)=cos 2 θ – greh 2 jaz. Uporabljajo se za izražanje trigonometričnih funkcij dvojnih kotov z enojnimi koti.
Kako najdete vrednosti sinusa in kosinusa za kote v različnih kvadrantih?
Predznaki sinusne in kosinusne funkcije so odvisni od kvadranta, v katerem leži kot:
- Prvi kvadrant: sin θ> 0 in cos θ> 0
- Drugi kvadrant: sin θ> 0 in cos θ <0
- Tretji kvadrant: sinθ <0 in cosθ < 0
- Četrti kvadrant: sinθ 0
