 #practiceLinkDiv { display: none !important; }
#practiceLinkDiv { display: none !important; }Algoritem povratnega brisanja je tesno povezan z Kruskalov algoritem . V Kruskalovem algoritmu naredimo naslednje: Razvrstimo robove po naraščajočem vrstnem redu njihovih uteži. Po sortiranju enega za drugim izbiramo robove v naraščajočem vrstnem redu. Trenutno izbrani rob vključimo, če z vključitvijo tega v vpeto drevo ne tvorimo nobenega cikla, dokler v vpetem drevesu ni robov V-1, kjer je V = število vozlišč.
V algoritmu Reverse Delete razvrstimo vse robove zmanjševanje vrstni red njihovih uteži. Po razvrščanju enega za drugim izbiramo robove v padajočem vrstnem redu. mi vključi trenutno izbrani rob, če izključitev trenutnega roba povzroči prekinitev povezave v trenutnem grafu . Glavna ideja je izbrisati rob, če njegov izbris ne povzroči prekinitve povezave grafa.
java stikalo int
Algoritem:
- Razvrsti vse robove grafa v nenaraščajočem vrstnem redu uteži robov.
- Inicializirajte MST kot izvirni graf in s 3. korakom odstranite dodatne robove.
- Izberite najtežji rob izmed preostalih robov in preverite, ali brisanje roba prekine povezavo grafa ali ne .
Če prekine povezavo, roba ne izbrišemo.
Sicer izbrišemo rob in nadaljujemo.
Ilustracija:
Naj razumemo z naslednjim primerom:
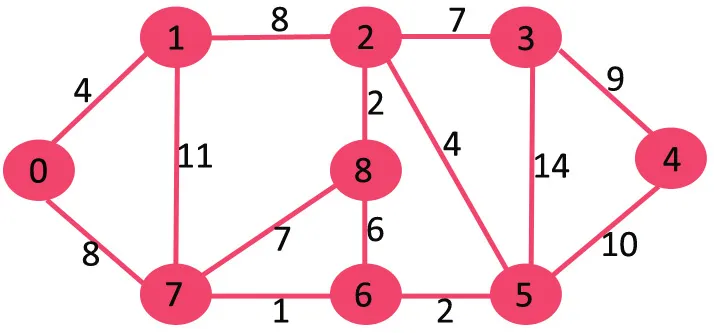
Če izbrišemo najvišji rob teže 14, graf ne postane nepovezan, zato ga odstranimo.
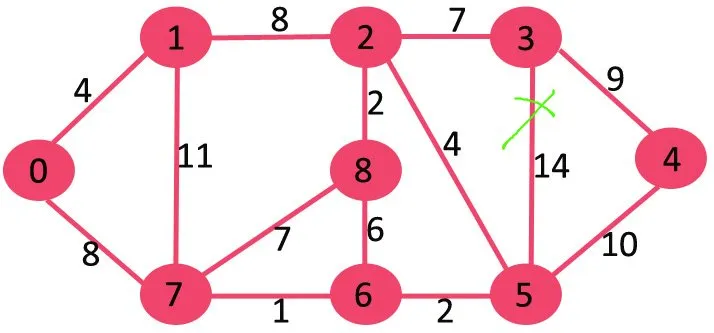
Nato izbrišemo 11, saj brisanje ne prekine povezave z grafom.
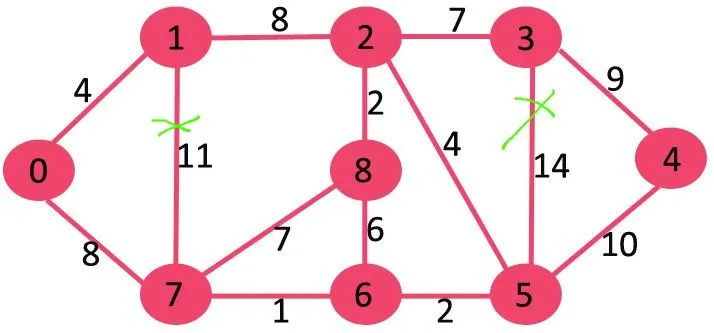
Nato izbrišemo 10, saj brisanje ne prekine povezave z grafom.

Naslednji je 9. Ne moremo izbrisati 9, saj brisanje povzroči prekinitev povezave.

Nadaljujemo po tej poti in naslednji robovi ostanejo v končnem MST.
Edges in MST
(3 4)
(0 7)
(2 3)
(2 5)
(0 1)
(5 6)
(2 8)
(6 7)
Opomba: V primeru enako težkih robov lahko izberemo kateri koli rob enakih težkih robov.
Priporočena praksa Algoritem za obratno brisanje za minimalno vpeto drevo Poskusite!Izvedba:
C++// C++ program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm #include
// Java program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm import java.util.*; // class to represent an edge class Edge implements Comparable<Edge> { int u v w; Edge(int u int v int w) { this.u = u; this.w = w; this.v = v; } public int compareTo(Edge other) { return (this.w - other.w); } } // Class to represent a graph using adjacency list // representation public class GFG { private int V; // No. of vertices private List<Integer>[] adj; private List<Edge> edges; @SuppressWarnings({ 'unchecked' 'deprecated' }) public GFG(int v) // Constructor { V = v; adj = new ArrayList[v]; for (int i = 0; i < v; i++) adj[i] = new ArrayList<Integer>(); edges = new ArrayList<Edge>(); } // function to Add an edge public void AddEdge(int u int v int w) { adj[u].add(v); // Add w to v’s list. adj[v].add(u); // Add w to v’s list. edges.add(new Edge(u v w)); } // function to perform dfs private void DFS(int v boolean[] visited) { // Mark the current node as visited and print it visited[v] = true; // Recur for all the vertices adjacent to // this vertex for (int i : adj[v]) { if (!visited[i]) DFS(i visited); } } // Returns true if given graph is connected else false private boolean IsConnected() { boolean[] visited = new boolean[V]; // Find all reachable vertices from first vertex DFS(0 visited); // If set of reachable vertices includes all // return true. for (int i = 1; i < V; i++) { if (visited[i] == false) return false; } return true; } // This function assumes that edge (u v) // exists in graph or not public void ReverseDeleteMST() { // Sort edges in increasing order on basis of cost Collections.sort(edges); int mst_wt = 0; // Initialize weight of MST System.out.println('Edges in MST'); // Iterate through all sorted edges in // decreasing order of weights for (int i = edges.size() - 1; i >= 0; i--) { int u = edges.get(i).u; int v = edges.get(i).v; // Remove edge from undirected graph adj[u].remove(adj[u].indexOf(v)); adj[v].remove(adj[v].indexOf(u)); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if (IsConnected() == false) { adj[u].add(v); adj[v].add(u); // This edge is part of MST System.out.println('(' + u + ' ' + v + ')'); mst_wt += edges.get(i).w; } } System.out.println('Total weight of MST is ' + mst_wt); } // Driver code public static void main(String[] args) { // create the graph given in above figure int V = 9; GFG g = new GFG(V); // making above shown graph g.AddEdge(0 1 4); g.AddEdge(0 7 8); g.AddEdge(1 2 8); g.AddEdge(1 7 11); g.AddEdge(2 3 7); g.AddEdge(2 8 2); g.AddEdge(2 5 4); g.AddEdge(3 4 9); g.AddEdge(3 5 14); g.AddEdge(4 5 10); g.AddEdge(5 6 2); g.AddEdge(6 7 1); g.AddEdge(6 8 6); g.AddEdge(7 8 7); g.ReverseDeleteMST(); } } // This code is contributed by Prithi_Dey
# Python3 program to find Minimum Spanning Tree # of a graph using Reverse Delete Algorithm # Graph class represents a directed graph # using adjacency list representation class Graph: def __init__(self v): # No. of vertices self.v = v self.adj = [0] * v self.edges = [] for i in range(v): self.adj[i] = [] # function to add an edge to graph def addEdge(self u: int v: int w: int): self.adj[u].append(v) # Add w to v’s list. self.adj[v].append(u) # Add w to v’s list. self.edges.append((w (u v))) def dfs(self v: int visited: list): # Mark the current node as visited and print it visited[v] = True # Recur for all the vertices adjacent to # this vertex for i in self.adj[v]: if not visited[i]: self.dfs(i visited) # Returns true if graph is connected # Returns true if given graph is connected else false def connected(self): visited = [False] * self.v # Find all reachable vertices from first vertex self.dfs(0 visited) # If set of reachable vertices includes all # return true. for i in range(1 self.v): if not visited[i]: return False return True # This function assumes that edge (u v) # exists in graph or not def reverseDeleteMST(self): # Sort edges in increasing order on basis of cost self.edges.sort(key = lambda a: a[0]) mst_wt = 0 # Initialize weight of MST print('Edges in MST') # Iterate through all sorted edges in # decreasing order of weights for i in range(len(self.edges) - 1 -1 -1): u = self.edges[i][1][0] v = self.edges[i][1][1] # Remove edge from undirected graph self.adj[u].remove(v) self.adj[v].remove(u) # Adding the edge back if removing it # causes disconnection. In this case this # edge becomes part of MST. if self.connected() == False: self.adj[u].append(v) self.adj[v].append(u) # This edge is part of MST print('( %d %d )' % (u v)) mst_wt += self.edges[i][0] print('Total weight of MST is' mst_wt) # Driver Code if __name__ == '__main__': # create the graph given in above figure V = 9 g = Graph(V) # making above shown graph g.addEdge(0 1 4) g.addEdge(0 7 8) g.addEdge(1 2 8) g.addEdge(1 7 11) g.addEdge(2 3 7) g.addEdge(2 8 2) g.addEdge(2 5 4) g.addEdge(3 4 9) g.addEdge(3 5 14) g.addEdge(4 5 10) g.addEdge(5 6 2) g.addEdge(6 7 1) g.addEdge(6 8 6) g.addEdge(7 8 7) g.reverseDeleteMST() # This code is contributed by # sanjeev2552
// C# program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm using System; using System.Collections.Generic; // class to represent an edge public class Edge : IComparable<Edge> { public int u v w; public Edge(int u int v int w) { this.u = u; this.v = v; this.w = w; } public int CompareTo(Edge other) { return this.w.CompareTo(other.w); } } // Graph class represents a directed graph // using adjacency list representation public class Graph { private int V; // No. of vertices private List<int>[] adj; private List<Edge> edges; public Graph(int v) // Constructor { V = v; adj = new List<int>[ v ]; for (int i = 0; i < v; i++) adj[i] = new List<int>(); edges = new List<Edge>(); } // function to Add an edge public void AddEdge(int u int v int w) { adj[u].Add(v); // Add w to v’s list. adj[v].Add(u); // Add w to v’s list. edges.Add(new Edge(u v w)); } // function to perform dfs private void DFS(int v bool[] visited) { // Mark the current node as visited and print it visited[v] = true; // Recur for all the vertices adjacent to // this vertex foreach(int i in adj[v]) { if (!visited[i]) DFS(i visited); } } // Returns true if given graph is connected else false private bool IsConnected() { bool[] visited = new bool[V]; // Find all reachable vertices from first vertex DFS(0 visited); // If set of reachable vertices includes all // return true. for (int i = 1; i < V; i++) { if (visited[i] == false) return false; } return true; } // This function assumes that edge (u v) // exists in graph or not public void ReverseDeleteMST() { // Sort edges in increasing order on basis of cost edges.Sort(); int mst_wt = 0; // Initialize weight of MST Console.WriteLine('Edges in MST'); // Iterate through all sorted edges in // decreasing order of weights for (int i = edges.Count - 1; i >= 0; i--) { int u = edges[i].u; int v = edges[i].v; // Remove edge from undirected graph adj[u].Remove(v); adj[v].Remove(u); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if (IsConnected() == false) { adj[u].Add(v); adj[v].Add(u); // This edge is part of MST Console.WriteLine('({0} {1})' u v); mst_wt += edges[i].w; } } Console.WriteLine('Total weight of MST is {0}' mst_wt); } } class GFG { // Driver code static void Main(string[] args) { // create the graph given in above figure int V = 9; Graph g = new Graph(V); // making above shown graph g.AddEdge(0 1 4); g.AddEdge(0 7 8); g.AddEdge(1 2 8); g.AddEdge(1 7 11); g.AddEdge(2 3 7); g.AddEdge(2 8 2); g.AddEdge(2 5 4); g.AddEdge(3 4 9); g.AddEdge(3 5 14); g.AddEdge(4 5 10); g.AddEdge(5 6 2); g.AddEdge(6 7 1); g.AddEdge(6 8 6); g.AddEdge(7 8 7); g.ReverseDeleteMST(); } } // This code is contributed by cavi4762
// Javascript program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm // Graph class represents a directed graph // using adjacency list representation class Graph { // Constructor constructor(V) { this.V = V; this.adj = []; this.edges = []; for (let i = 0; i < V; i++) { this.adj[i] = []; } } // function to add an edge to graph addEdge(u v w) { this.adj[u].push(v);// Add w to v’s list. this.adj[v].push(u);// Add w to v’s list. this.edges.push([w [u v]]); } DFS(v visited) { // Mark the current node as visited and print it visited[v] = true; for (const i of this.adj[v]) { if (!visited[i]) { this.DFS(i visited); } } } // Returns true if given graph is connected else false isConnected() { const visited = []; for (let i = 0; i < this.V; i++) { visited[i] = false; } // Find all reachable vertices from first vertex this.DFS(0 visited); // If set of reachable vertices includes all // return true. for (let i = 1; i < this.V; i++) { if (!visited[i]) { return false; } } return true; } // This function assumes that edge (u v) // exists in graph or not reverseDeleteMST() { // Sort edges in increasing order on basis of cost this.edges.sort((a b) => a[0] - b[0]); let mstWt = 0;// Initialize weight of MST console.log('Edges in MST'); // Iterate through all sorted edges in // decreasing order of weights for (let i = this.edges.length - 1; i >= 0; i--) { const [u v] = this.edges[i][1]; // Remove edge from undirected graph this.adj[u] = this.adj[u].filter(x => x !== v); this.adj[v] = this.adj[v].filter(x => x !== u); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if (!this.isConnected()) { this.adj[u].push(v); this.adj[v].push(u); // This edge is part of MST console.log(`(${u} ${v})`); mstWt += this.edges[i][0]; } } console.log(`Total weight of MST is ${mstWt}`); } } // Driver code function main() { // create the graph given in above figure var V = 9; var g = new Graph(V); // making above shown graph g.addEdge(0 1 4); g.addEdge(0 7 8); g.addEdge(1 2 8); g.addEdge(1 7 11); g.addEdge(2 3 7); g.addEdge(2 8 2); g.addEdge(2 5 4); g.addEdge(3 4 9); g.addEdge(3 5 14); g.addEdge(4 5 10); g.addEdge(5 6 2); g.addEdge(6 7 1); g.addEdge(6 8 6); g.addEdge(7 8 7); g.reverseDeleteMST(); } main();
Izhod
Edges in MST (3 4) (0 7) (2 3) (2 5) (0 1) (5 6) (2 8) (6 7) Total weight of MST is 37
Časovna zahtevnost: O((E*(V+E)) + E log E) kjer je E število robov.
niz dolžine
Zahtevnost prostora: O(V+E) kjer je V število oglišč in E število robov. Za shranjevanje grafa uporabljamo seznam sosednosti, zato potrebujemo prostor, sorazmeren z O(V+E).
Opombe:
- Zgornja izvedba je preprosta/naivna izvedba algoritma Reverse Delete in jo je mogoče optimizirati na O(E log V (log log V)3) [Vir: en teden ]. Toda ta optimizirana časovna kompleksnost je še vedno manjša od Prim in Kruskal Algoritmi za MST.
- Zgornja izvedba spremeni prvotni graf. Ustvarimo lahko kopijo grafa, če je treba obdržati originalni graf.
Ustvari kviz
