• Pushdown avtomati so način za implementacijo CFG na enak način, kot načrtujemo DFA za navadno slovnico. DFA si lahko zapomni končno količino informacij, dlančnik pa si lahko zapomni neskončno količino informacij.
• Pushdown avtomati so preprosto NFA, razširjen z 'zunanjim skladovnim pomnilnikom'. Dodatek sklada se uporablja za zagotavljanje zmožnosti upravljanja pomnilnika »zadnji v, prvi ven« avtomatom Pushdown. Pushdown avtomati lahko shranijo neomejeno količino informacij na sklad. Lahko dostopa do omejene količine informacij v skladu. PDA lahko potisne element na vrh sklada in izskoči element z vrha sklada. Če želite prebrati element v sklad, je treba zgornje elemente odstraniti in izgubiti.
• PDA je močnejši od FA. Vsak jezik, ki je sprejemljiv za FA, je lahko sprejemljiv tudi za PDA. PDA sprejema tudi razred jezika, ki ga ne more sprejeti niti FA. Tako je PDA veliko boljši od FA.

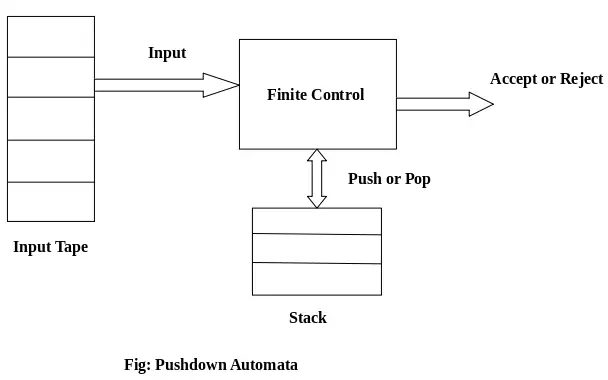
Komponente PDA:

Vhodni trak: Vhodni trak je razdeljen na veliko celic ali simbolov. Vnosna glava je samo za branje in se lahko premika samo od leve proti desni, en simbol naenkrat.

Končni nadzor: Končni kontrolnik ima nek kazalec, ki kaže na trenutni simbol, ki ga je treba prebrati.

Sklad: Sklad je struktura, v kateri lahko potiskamo in odstranjujemo elemente samo z enega konca. Ima neskončno velikost. V PDA se sklad uporablja za začasno shranjevanje predmetov.

Formalna definicija dlančnika:

PDA lahko definiramo kot zbirko 7 komponent:

V: končna množica stanj

∑: vhodni niz

C: simbol sklada, ki ga je mogoče potisniti in izstreliti iz sklada

q0: začetno stanje

datumski niz java

Z: začetni simbol, ki je v Γ.

F: niz končnih stanj

d: funkcija preslikave, ki se uporablja za premikanje iz trenutnega stanja v naslednje stanje.

Trenutni opis (ID)

ID je neuraden zapis o tem, kako dlančnik izračuna vhodni niz in se odloči, ali je niz sprejet ali zavrnjen.

Trenutni opis je trojka (q, w, α), kjer je:

q opisuje trenutno stanje.

notri opisuje preostali vnos.

dolgo nanizati

a opisuje vsebino sklada, zgoraj levo.

Oznaka vrtljive lopute:

Znak ⊢ opisuje notacijo vrtljive lopute in predstavlja eno potezo.

⊢* znak opisuje zaporedje potez.

na primer

(p, b, T) ⊢ (q, w, α)

V zgornjem primeru se med prehodom iz stanja p v q porabi vhodni simbol 'b', vrh sklada 'T' pa je predstavljen z novim nizom α.

Primer 1:

Oblikujte dlančnik za sprejem jezika aⁿb²ⁿ.

rešitev: V tem jeziku mora n številu a-jev slediti 2n številu b-jev. Zato bomo uporabili zelo preprosto logiko, in sicer če preberemo en sam 'a', bomo na sklad potisnili dva a. Takoj ko preberemo 'b', mora za vsak posamezen 'b' samo en 'a' izstopiti iz sklada.

kaj je jquery

ID je mogoče sestaviti na naslednji način:

 δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) 

Zdaj, ko preberemo b, bomo spremenili stanje iz q0 v q1 in začeli prikazovati ustrezen 'a'. torej

 δ(q0, b, a) = (q1, ε) 

Tako se bo ta postopek izpiranja 'b' ponovil, razen če so prebrani vsi simboli. Upoštevajte, da se pokanje zgodi samo v stanju q1.

 δ(q1, b, a) = (q1, ε) 

Ko preberete vse b-je, bi morali vsi ustrezni a-ji izpasti. Ko torej beremo ε kot vhodni simbol, potem v skladu ne bi smelo biti ničesar. Zato bo poteza:

 δ(q1, ε, Z) = (q2, ε) 

Kje

python razvrščena tuple

PDA = ({q0, q1, q2}, {a, b}, {a, Z}, δ, q0, Z, {q2})

ID lahko povzamemo kot:

 δ(q0, a, Z) = (q0, aaZ) δ(q0, a, a) = (q0, aaa) δ(q0, b, a) = (q1, ε) δ(q1, b, a) = (q1, ε) δ(q1, ε, Z) = (q2, ε) 

Zdaj bomo simulirali ta PDA za vhodni niz 'aaabbbbbb'.

 δ(q0, aaabbbbbb, Z) ⊢ δ(q0, aabbbbbb, aaZ) ⊢ δ(q0, abbbbbb, aaaaZ) ⊢ δ(q0, bbbbbb, aaaaaaZ) ⊢ δ(q1, bbbbb, aaaaaZ) ⊢ δ(q1, bbbb, aaaaZ) ⊢ δ(q1, bbb, aaaZ) ⊢ δ(q1, bb, aaZ) ⊢ δ(q1, b, aZ) ⊢ δ(q1, ε, Z) ⊢ δ(q2, ε) ACCEPT 

Primer 2:

Oblikujte dlančnik za sprejem jezika 0ⁿ1^m0ⁿ.

rešitev: V tem dlančniku n številu 0 sledi poljubno število 1, ki mu sledi n število 0. Zato bo logika zasnove takšnega dlančnika naslednja:

Potisnite vse 0 na sklad, ko naletite na prve 0. Potem, če preberemo 1, ne naredimo ničesar. Nato preberite 0 in ob vsakem branju 0 odstranite eno 0 iz sklada.

Na primer:

Ta scenarij je mogoče zapisati v obliki ID kot:

 δ(q0, 0, Z) = δ(q0, 0Z) δ(q0, 0, 0) = δ(q0, 00) δ(q0, 1, 0) = δ(q1, 0) δ(q0, 1, 0) = δ(q1, 0) δ(q1, 0, 0) = δ(q1, ε) δ(q0, ε, Z) = δ(q2, Z) (ACCEPT state) 

Sedaj bomo simulirali ta PDA za vhodni niz '0011100'.

 δ(q0, 0011100, Z) ⊢ δ(q0, 011100, 0Z) ⊢ δ(q0, 11100, 00Z) ⊢ δ(q0, 1100, 00Z) ⊢ δ(q1, 100, 00Z) ⊢ δ(q1, 00, 00Z) ⊢ δ(q1, 0, 0Z) ⊢ δ(q1, ε, Z) ⊢ δ(q2, Z) ACCEPT