Naključni je modul, ki je prisoten v knjižnici NumPy. Ta modul vsebuje funkcije, ki se uporabljajo za generiranje naključnih števil. Ta modul vsebuje nekaj preprostih metod generiranja naključnih podatkov, nekaj funkcij permutacije in porazdelitve ter funkcij naključnega generiranja.
Vse funkcije v naključnem modulu so naslednje:
Preprosti naključni podatki
Obstajajo naslednje funkcije preprostih naključnih podatkov:
1) p.naključno.rand(d0, d1, ..., dn)
Ta funkcija naključnega modula se uporablja za ustvarjanje naključnih števil ali vrednosti v dani obliki.
primer:
import numpy as np a=np.random.rand(5,2) a
Izhod:
array([[0.74710182, 0.13306399], [0.01463718, 0.47618842], [0.98980426, 0.48390004], [0.58661785, 0.62895758], [0.38432729, 0.90384119]])
2) np.random.randn(d0, d1, ..., dn)
Ta funkcija naključnega modula vrne vzorec iz 'standardne normalne' porazdelitve.
primer:
končna ključna beseda v Javi
import numpy as np a=np.random.randn(2,2) a
Izhod:
array([[ 1.43327469, -0.02019121], [ 1.54626422, 1.05831067]]) b=np.random.randn() b -0.3080190768904835
3) np.random.randint(nizko[, visoko, velikost, dtip])
Ta funkcija naključnega modula se uporablja za generiranje naključnih celih števil od vključujočega (nizkega) do izključujočega (visokega).
primer:
import numpy as np a=np.random.randint(3, size=10) a
Izhod:
array([1, 1, 1, 2, 0, 0, 0, 0, 0, 0])
4) np.random.random_integers(low[, high, size])
Ta funkcija naključnega modula se uporablja za generiranje naključnih celih števil tipa np.int med nizko in visoko.
primer:
import numpy as np a=np.random.random_integers(3) a b=type(np.random.random_integers(3)) b c=np.random.random_integers(5, size=(3,2)) c
Izhod:
2 array([[1, 1], [2, 5], [1, 3]])
5) np.random.random_sample([velikost])
Ta funkcija naključnega modula se uporablja za generiranje naključnega števila lebdečih v polodprtem intervalu [0,0, 1,0).
primer:
import numpy as np a=np.random.random_sample() a b=type(np.random.random_sample()) b c=np.random.random_sample((5,)) c
Izhod:
0.09250360565571492 array([0.34665418, 0.47027209, 0.75944969, 0.37991244, 0.14159746])
6) np.random.random([velikost])
Ta funkcija naključnega modula se uporablja za generiranje naključnega števila lebdečih v polodprtem intervalu [0,0, 1,0).
primer:
import numpy as np a=np.random.random() a b=type(np.random.random()) b c=np.random.random((5,)) c
Izhod:
0.008786953974334155 array([0.05530122, 0.59133394, 0.17258794, 0.6912388 , 0.33412534])
7) np.random.ranf([velikost])
Ta funkcija naključnega modula se uporablja za generiranje naključnega števila lebdečih v polodprtem intervalu [0,0, 1,0).
primer:
import numpy as np a=np.random.ranf() a b=type(np.random.ranf()) b c=np.random.ranf((5,)) c
Izhod:
0.2907792098474542 array([0.34084881, 0.07268237, 0.38161256, 0.46494681, 0.88071377])
8) np.random.sample([velikost])
Ta funkcija naključnega modula se uporablja za generiranje naključnega števila lebdečih v polodprtem intervalu [0,0, 1,0).
primer:
import numpy as np a=np.random.sample() a b=type(np.random.sample()) b c=np.random.sample((5,)) c
Izhod:
0.012298209913766511 array([0.71878544, 0.11486169, 0.38189074, 0.14303308, 0.07217287])
9) np.random.choice(a[, velikost, zamenjaj, p])
Ta funkcija naključnega modula se uporablja za ustvarjanje naključnega vzorca iz dane 1-D matrike.
primer:
import numpy as np a=np.random.choice(5,3) a b=np.random.choice(5,3, p=[0.2, 0.1, 0.4, 0.2, 0.1]) b
Izhod:
array([0, 3, 4]) array([2, 2, 2], dtype=int64)
10) np.random.bytes(dolžina)
Ta funkcija naključnega modula se uporablja za ustvarjanje naključnih bajtov.
primer:
import numpy as np a=np.random.bytes(7) a
Izhod:
'nQx08x83xf9xdex8a'
Permutacije
Obstajajo naslednje funkcije permutacij:
1) np.random.shuffle()
Ta funkcija se uporablja za spreminjanje zaporedja na mestu s premešanjem njegove vsebine.
primer:
import numpy as np a=np.arange(12) a np.random.shuffle(a) a
Izhod:
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]) array([10, 3, 2, 4, 5, 8, 0, 9, 1, 11, 7, 6])
2) np.random.permutation()
Ta funkcija naključno permutira zaporedje ali vrne permutiran obseg.
primer:
import numpy as np a=np.random.permutation(12) a
Izhod:
array([ 8, 7, 3, 11, 6, 0, 9, 10, 2, 5, 4, 1])
Distribucije
Obstajajo naslednje funkcije permutacij:
1) beta(a, b[, velikost])
Ta funkcija se uporablja za črpanje vzorcev iz beta distribucije.
primer:
def setup(self): self.dist = dist.beta self.cargs = [] self.ckwd = dict(alpha=2, beta=3) self.np_rand_fxn = numpy.random.beta self.np_args = [2, 3] self.np_kwds = dict()
2) binom (n, p[, velikost])
Ta funkcija se uporablja za črpanje vzorca iz binomske porazdelitve.
primer:
import numpy as np n, p = 10, .6 s1= np.random.binomial(n, p, 10) s1
Izhod:
array([6, 7, 7, 9, 3, 7, 8, 6, 6, 4])
3) hikvadrat(df[, velikost])
Ta funkcija se uporablja za črpanje vzorca iz binomske porazdelitve.
primer:
import numpy as np np.random.chisquare(2,4) sum(np.random.binomial(9, 0.1, 20000) == 0)/20000.
Izhod:
array([6, 7, 7, 9, 3, 7, 8, 6, 6, 4])
4) dirichlet(alfa[, velikost])
Ta funkcija se uporablja za risanje vzorca iz Dirichletove porazdelitve.
primer:
Import numpy as np import matplotlib.pyplot as plt s1 = np.random.dirichlet((10, 5, 3), 20).transpose() plt.barh(range(20), s1[0]) plt.barh(range(20), s1[1], left=s1[0], color='g') plt.barh(range(20), s1[2], left=s1[0]+s1[1], color='r') plt.title('Lengths of Strings') plt.show()
Izhod:
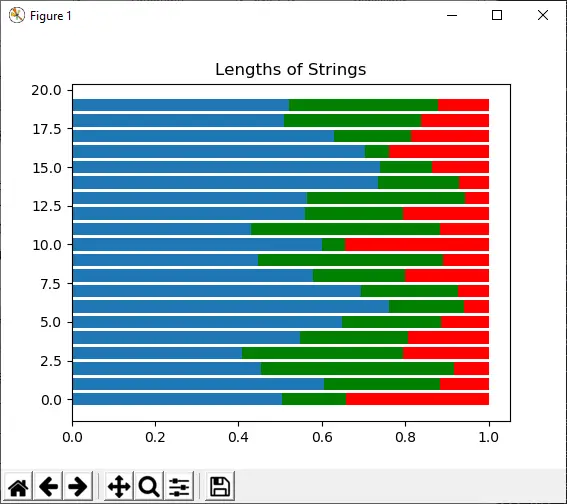
5) eksponentno ([lestvica, velikost])
Ta funkcija se uporablja za črpanje vzorca iz eksponentne porazdelitve.
primer:
def __init__(self, sourceid, targetid): self.__type = 'Transaction' self.id = uuid4() self.source = sourceid self.target = targetid self.date = self._datetime.date(start=2015, end=2019) self.time = self._datetime.time() if random() <0.05: self.amount="self._numbers.between(100000," 1000000) if random() < 0.15: self.currency="self._business.currency_iso_code()" else: pre> <p> <strong>6) f(dfnum, dfden[, size])</strong> </p> <p>This function is used to draw sample from an F distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np dfno= 1. dfden = 48. s1 = np.random.f(dfno, dfden, 10) np.sort(s1) </pre> <p> <strong>Output:</strong> </p> <pre> array([0.00264041, 0.04725478, 0.07140803, 0.19526217, 0.23979 , 0.24023478, 0.63141254, 0.95316446, 1.40281789, 1.68327507]) </pre> <p> <strong>7) gamma(shape[, scale, size])</strong> </p> <p>This function is used to draw sample from a Gamma distribution </p> <p> <strong>Example:</strong> </p> <pre> import numpy as np shape, scale = 2., 2. s1 = np.random.gamma(shape, scale, 1000) import matplotlib.pyplot as plt import scipy.special as spss count, bins, ignored = plt.hist(s1, 50, density=True) a = bins**(shape-1)*(np.exp(-bins/scale) / (spss.gamma(shape)*scale**shape)) plt.plot(bins, a, linewidth=2, color='r') plt.show() </pre> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-2.webp" alt="numpy.random in Python"> <p> <strong>8) geometric(p[, size])</strong> </p> <p>This function is used to draw sample from a geometric distribution. </p> <p> <strong>Example:</strong> </p> <pre> import numpy as np a = np.random.geometric(p=0.35, size=10000) (a == 1).sum() / 1000 </pre> <p> <strong>Output:</strong> </p> <pre> 3. </pre> <p> <strong>9) gumbel([loc, scale, size])</strong> </p> <p>This function is used to draw sample from a Gumble distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np lov, scale = 0, 0.2 s1 = np.random.gumbel(loc, scale, 1000) import matplotlib.pyplot as plt count, bins, ignored = plt.hist(s1, 30, density=True) plt.plot(bins, (1/beta)*np.exp(-(bins - loc)/beta)* np.exp( -np.exp( -(bins - loc) /beta) ),linewidth=2, color='r') plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-3.webp" alt="numpy.random in Python"> <p> <strong>10) hypergeometric(ngood, nbad, nsample[, size])</strong> </p> <p>This function is used to draw sample from a Hypergeometric distribution. </p> <p> <strong>Example:</strong> </p> <pre> import numpy as np good, bad, samp = 100, 2, 10 s1 = np.random.hypergeometric(good, bad, samp, 1000) plt.hist(s1) plt.show() </pre> <p> <strong>Output:</strong> </p> <pre> (array([ 13., 0., 0., 0., 0., 163., 0., 0., 0., 824.]), array([ 8. , 8.2, 8.4, 8.6, 8.8, 9. , 9.2, 9.4, 9.6, 9.8, 10. ]), <a 10 list of patch objects>) </a></pre> <p><img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-4.webp" alt="numpy.random in Python"></p> <p> <strong>11) laplace([loc, scale, size])</strong> </p> <p>This function is used to draw sample from the Laplace or double exponential distribution with specified location and scale.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np location, scale = 0., 2. s = np.random.laplace(location, scale, 10) s </pre> <p> <strong>Output:</strong> </p> <pre> array([-2.77127948, -1.46401453, -0.03723516, -1.61223942, 2.29590691, 1.74297722, 1.49438411, 0.30325513, -0.15948891, -4.99669747]) </pre> <p> <strong>12) logistic([loc, scale, size])</strong> </p> <p>This function is used to draw sample from logistic distribution. </p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt location, scale = 10, 1 s1 = np.random.logistic(location, scale, 10000) count, bins, ignored = plt.hist(s1, bins=50) count bins ignored plt.show() </pre> <p> <strong>Output:</strong> </p> <pre> array([1.000e+00, 1.000e+00, 1.000e+00, 0.000e+00, 1.000e+00, 1.000e+00, 1.000e+00, 5.000e+00, 7.000e+00, 1.100e+01, 1.800e+01, 3.500e+01, 5.300e+01, 6.700e+01, 1.150e+02, 1.780e+02, 2.300e+02, 3.680e+02, 4.910e+02, 6.400e+02, 8.250e+02, 9.100e+02, 9.750e+02, 1.039e+03, 9.280e+02, 8.040e+02, 6.530e+02, 5.240e+02, 3.380e+02, 2.470e+02, 1.650e+02, 1.150e+02, 8.500e+01, 6.400e+01, 3.300e+01, 1.600e+01, 2.400e+01, 1.400e+01, 4.000e+00, 5.000e+00, 2.000e+00, 2.000e+00, 1.000e+00, 1.000e+00, 0.000e+00, 1.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 1.000e+00]) array([ 0.50643911, 0.91891814, 1.33139717, 1.7438762 , 2.15635523, 2.56883427, 2.9813133 , 3.39379233, 3.80627136, 4.2187504 , 4.63122943, 5.04370846, 5.45618749, 5.86866652, 6.28114556, 6.69362459, 7.10610362, 7.51858265, 7.93106169, 8.34354072, 8.75601975, 9.16849878, 9.58097781, 9.99345685, 10.40593588, 10.81841491, 11.23089394, 11.64337298, 12.05585201, 12.46833104, 12.88081007, 13.2932891 , 13.70576814, 14.11824717, 14.5307262 , 14.94320523, 15.35568427, 15.7681633 , 16.18064233, 16.59312136, 17.00560039, 17.41807943, 17.83055846, 18.24303749, 18.65551652, 19.06799556, 19.48047459, 19.89295362, 20.30543265, 20.71791168, 21.13039072]) <a 50 list of patch objects> </a></pre> <p><img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-5.webp" alt="numpy.random in Python"></p> <p> <strong>13) lognormal([mean, sigma, size])</strong> </p> <p>This function is used to draw sample from a log-normal distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np mu, sigma = 2., 1. s1 = np.random.lognormal(mu, sigma, 1000) import matplotlib.pyplot as plt count, bins, ignored = plt.hist(s1, 100, density=True, ) a = np.linspace(min(bins), max(bins), 10000) pdf = (np.exp(-(np.log(a) - mu)**2 / (2 * sigma**2))/ (a * sigma * np.sqrt(2 * np.pi))) plt.plot(a, pdf, linewidth=2, color='r') plt.axis('tight') plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-6.webp" alt="numpy.random in Python"> <p> <strong>14) logseries(p[, size])</strong> </p> <p>This function is used to draw sample from a logarithmic distribution. </p> <p> <strong>Example:</strong> </p> <pre> import numpy as np x = .6 s1 = np.random.logseries(x, 10000) count, bins, ignored = plt.hist(s1) def logseries(k, p): return -p**k/(k*log(1-p)) plt.plot(bins, logseries(bins, x)*count.max()/logseries(bins, a).max(), 'r') plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-7.webp" alt="numpy.random in Python"> <p> <strong>15) multinomial(n, pvals[, size])</strong> </p> <p>This function is used to draw sample from a multinomial distribution. </p> <p> <strong>Example:</strong> </p> <pre> import numpy as np np.random.multinomial(20, [1/6.]*6, size=1) </pre> <p> <strong>Output:</strong> </p> <pre> array([[4, 2, 5, 5, 3, 1]]) </pre> <p> <strong>16) multivariate_normal(mean, cov[, size, ...)</strong> </p> <p>This function is used to draw sample from a multivariate normal distribution. </p> <p> <strong>Example:</strong> </p> <pre> import numpy as np mean = (1, 2) coveriance = [[1, 0], [0, 100]] import matplotlib.pyplot as plt a, b = np.random.multivariate_normal(mean, coveriance, 5000).T plt.plot(a, b, 'x') plt.axis('equal'023 030 ) plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-8.webp" alt="numpy.random in Python"> <p> <strong>17) negative_binomial(n, p[, size])</strong> </p> <p>This function is used to draw sample from a negative binomial distribution. </p> <p> <strong>Example:</strong> </p> <pre> import numpy as np s1 = np.random.negative_binomial(1, 0.1, 100000) for i in range(1, 11): probability = sum(s1 <i) 36 100000. print i, 'wells drilled, probability of one success=", probability </pre> <p> <strong>Output:</strong> </p> <pre> 1 wells drilled, probability of one success = 0 2 wells drilled, probability of one success = 0 3 wells drilled, probability of one success = 0 4 wells drilled, probability of one success = 0 5 wells drilled, probability of one success = 0 6 wells drilled, probability of one success = 0 7 wells drilled, probability of one success = 0 8 wells drilled, probability of one success = 0 9 wells drilled, probability of one success = 0 10 wells drilled, probability of one success = 0 </pre> <p > <strong>18) noncentral_chisquare(df, nonc[, size])</strong> </p> <p>This function is used to draw sample from a noncentral chi-square distribution. </p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt val = plt.hist(np.random.noncentral_chisquare(3, 25, 100000), bins=200, normed=True) plt.show() </pre> <p> <strong>Output:</strong> </p> <img src=" techcodeview.com img numpy-tutorial numpy-random-python-9.webp' alt="numpy.random in Python"> <p> <strong>19) normal([loc, scale, size])</strong> </p> <p>This function is used to draw sample from a normal distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt mu, sigma = 0, 0.2 # mean and standard deviation s1 = np.random.normal(mu, sigma, 1000) abs(mu - np.mean(s1)) <0.01 1 abs(sigma - np.std(s1, ddof="1))" < 0.01 count, bins, ignored="plt.hist(s1," 30, density="True)" plt.plot(bins, (sigma * np.sqrt(2 np.pi)) *np.exp( (bins mu)**2 (2 sigma**2) ), linewidth="2," color="r" ) plt.show() pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-10.webp" alt="numpy.random in Python"> <p> <strong>20) pareto(a[, size])</strong> </p> <p>This function is used to draw samples from a Lomax or Pareto II with specified shape.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt b, m1 = 3., 2. # shape and mode s1 = (np.random.pareto(b, 1000) + 1) * m1 count, bins, _ = plt.hist(s1, 100, density=True) fit = b*m**b / bins**(b+1) plt.plot(bins, max(count)*fit/max(fit), linewidth=2, color='r') plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-11.webp" alt="numpy.random in Python"> <p> <strong>21) power(a[, size])</strong> </p> <p>This function is used to draw samples in [0, 1] from a power distribution with positive exponent a-1.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np x = 5. # shape samples = 1000 s1 = np.random.power(x, samples) import matplotlib.pyplot as plt count, bins, ignored = plt.hist(s1, bins=30) a = np.linspace(0, 1, 100) b = x*a**(x-1.) density_b = samples*np.diff(bins)[0]*b plt.plot(a, density_b) plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-12.webp" alt="numpy.random in Python"> <p> <strong>22) rayleigh([scale, size])</strong> </p> <p>This function is used to draw sample from a Rayleigh distribution.</p> <p> <strong>Example:</strong> </p> <pre> val = hist(np.random.rayleigh(3, 100000), bins=200, density=True) meanval = 1 modeval = np.sqrt(2 / np.pi) * meanval s1 = np.random.rayleigh(modeval, 1000000) 100.*sum(s1>3)/1000000. </pre> <p> <strong>Output:</strong> </p> <pre> 0.087300000000000003 </pre> <p><img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-13.webp" alt="numpy.random in Python"></p> <p> <strong>23) standard_cauchy([size])</strong> </p> <p>This function is used to draw sample from a standard Cauchy distribution with mode=0.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt s1 = np.random.standard_cauchy(1000000) s1 = s1[(s1>-25) & (s1<25)] # truncate distribution so it plots well plt.hist(s1, bins="100)" plt.show() < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-14.webp" alt="numpy.random in Python"> <p> <strong>24) standard_exponential([size])</strong> </p> <p>This function is used to draw sample from a standard exponential distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np n = np.random.standard_exponential((2, 7000)) </pre> <p> <strong>Output:</strong> </p> <pre> array([[0.53857931, 0.181262 , 0.20478701, ..., 3.66232881, 1.83882709, 1.77963295], [0.65163973, 1.40001955, 0.7525986 , ..., 0.76516523, 0.8400617 , 0.88551011]]) </pre> <p> <strong>25) standard_gamma([size])</strong> </p> <p>This function is used to draw sample from a standard Gamma distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np shape, scale = 2., 1. s1 = np.random.standard_gamma(shape, 1000000) import matplotlib.pyplot as plt import scipy.special as sps count1, bins1, ignored1 = plt.hist(s, 50, density=True) y = bins1**(shape-1) * ((np.exp(-bins1/scale))/ (sps.gamma(shape) * scale**shape)) plt.plot(bins1, y, linewidth=2, color='r') plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-15.webp" alt="numpy.random in Python"> <p> <strong>26) standard_normal([size])</strong> </p> <p>This function is used to draw sample from a standard Normal distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt s1= np.random.standard_normal(8000) s1 q = np.random.standard_normal(size=(3, 4, 2)) q </pre> <p> <strong>Output:</strong> </p> <pre> array([-3.14907597, 0.95366265, -1.20100026, ..., 3.47180222, 0.9608679 , 0.0774319 ]) array([[[ 1.55635461, -1.29541713], [-1.50534663, -0.02829194], [ 1.03949348, -0.26128132], [ 1.51921798, 0.82136178]], [[-0.4011052 , -0.52458858], [-1.31803814, 0.37415379], [-0.67077365, 0.97447018], [-0.20212115, 0.67840888]], [[ 1.86183474, 0.19946562], [-0.07376021, 0.84599701], [-0.84341386, 0.32081667], [-3.32016062, -1.19029818]]]) </pre> <p> <strong>27) standard_t(df[, size])</strong> </p> <p>This function is used to draw sample from a standard Student's distribution with df degree of freedom.</p> <p> <strong>Example:</strong> </p> <pre> intake = np.array([5260., 5470, 5640, 6180, 6390, 6515, 6805, 7515,8230,8770]) s1 = np.random.standard_t(10, size=100000) np.mean(intake) intake.std(ddof=1) t = (np.mean(intake)-7725)/(intake.std(ddof=1)/np.sqrt(len(intake))) h = plt.hist(s1, bins=100, density=True) np.sum(s1<t) float(len(s1)) plt.show() < pre> <p> <strong>Output:</strong> </p> <pre> 6677.5 1174.1101831694598 0.00864 </pre> <p><img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-16.webp" alt="numpy.random in Python"></p> <p> <strong>28) triangular(left, mode, right[, size])</strong> </p> <p>This function is used to draw sample from a triangular distribution over the interval.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt h = plt.hist(np.random.triangular(-4, 0, 8, 1000000), bins=300,density=True) plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-17.webp" alt="numpy.random in Python"> <p> <strong>29) uniform([low, high, size])</strong> </p> <p>This function is used to draw sample from a uniform distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt s1 = np.random.uniform(-1,0,1000) np.all(s1 >= -1) np.all(s1 <0) count, bins, ignored="plt.hist(s1," 15, density="True)" plt.plot(bins, np.ones_like(bins), linewidth="2," color="r" ) plt.show() < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-18.webp" alt="numpy.random in Python"> <p> <strong>30) vonmises(m1, m2[, size])</strong> </p> <p>This function is used to draw sample from a von Mises distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt m1, m2 = 0.0, 4.0 s1 = np.random.vonmises(m1, m2, 1000) from scipy.special import i0 plt.hist(s1, 50, density=True) x = np.linspace(-np.pi, np.pi, num=51) y = np.exp(m2*np.cos(x-m1))/(2*np.pi*i0(m2)) plt.plot(x, y, linewidth=2, color='r') plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-19.webp" alt="numpy.random in Python"> <p> <strong>31) wald(mean, scale[, size])</strong> </p> <p>This function is used to draw sample from a Wald, or inverse Gaussian distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt h = plt.hist(np.random.wald(3, 3, 100000), bins=250, density=True) plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-20.webp" alt="numpy.random in Python"> <p> <strong>32) weibull(a[, size])</strong> </p> <p>This function is used to draw sample from a Weibull distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt from scipy import special x=2.0 s=np.random.weibull(x, 1000) a = np.arange(1, 100.)/50. def weib(x, n, a): return (a/n)*(x/n)**np.exp(-(x/n)**a) count, bins, ignored = plt.hist(np.random.weibull(5.,1000)) a= np.arange(1,100.)/50. scale = count.max()/weib(x, 1., 5.).max() scale = count.max()/weib(a, 1., 5.).max() plt.plot(x, weib(x, 1., 5.)*scale) plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-21.webp" alt="numpy.random in Python"> <p> <strong>33) zipf(a[, size])</strong> </p> <p>This function is used to draw sample from a Zipf distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt from scipy import special x=2.0 s=np.random.zipf(x, 1000) count, bins, ignored = plt.hist(s[s<50], 50, density="True)" a="np.arange(1.," 50.) b="a**(-x)" special.zetac(x) plt.plot(a, max(b), linewidth="2," color="r" ) plt.show() < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-22.webp" alt="numpy.random in Python"> <hr></50],></pre></0)></pre></t)></pre></25)]></pre></0.01></pre></i)></pre></0.05:>
Izhod:
array([0.00264041, 0.04725478, 0.07140803, 0.19526217, 0.23979 , 0.24023478, 0.63141254, 0.95316446, 1.40281789, 1.68327507])
7) gama (oblika [, merilo, velikost])
Ta funkcija se uporablja za črpanje vzorca iz porazdelitve gama
primer:
import numpy as np shape, scale = 2., 2. s1 = np.random.gamma(shape, scale, 1000) import matplotlib.pyplot as plt import scipy.special as spss count, bins, ignored = plt.hist(s1, 50, density=True) a = bins**(shape-1)*(np.exp(-bins/scale) / (spss.gamma(shape)*scale**shape)) plt.plot(bins, a, linewidth=2, color='r') plt.show()

8) geometrijski (p[, velikost])
Ta funkcija se uporablja za risanje vzorca iz geometrijske porazdelitve.
primer:
import numpy as np a = np.random.geometric(p=0.35, size=10000) (a == 1).sum() / 1000
Izhod:
3.
9) gumbel([lokacija, lestvica, velikost])
Ta funkcija se uporablja za črpanje vzorca iz distribucije Gumble.
primer:
import numpy as np lov, scale = 0, 0.2 s1 = np.random.gumbel(loc, scale, 1000) import matplotlib.pyplot as plt count, bins, ignored = plt.hist(s1, 30, density=True) plt.plot(bins, (1/beta)*np.exp(-(bins - loc)/beta)* np.exp( -np.exp( -(bins - loc) /beta) ),linewidth=2, color='r') plt.show()
Izhod:

10) hipergeometrično (ndobro, nslabo, nvzorec[, velikost])
Ta funkcija se uporablja za risanje vzorca iz hipergeometrične porazdelitve.
primer:
import numpy as np good, bad, samp = 100, 2, 10 s1 = np.random.hypergeometric(good, bad, samp, 1000) plt.hist(s1) plt.show()
Izhod:
uporabo interneta
(array([ 13., 0., 0., 0., 0., 163., 0., 0., 0., 824.]), array([ 8. , 8.2, 8.4, 8.6, 8.8, 9. , 9.2, 9.4, 9.6, 9.8, 10. ]), <a 10 list of patch objects>) </a>

11) laplace([lokacija, merilo, velikost])
Ta funkcija se uporablja za risanje vzorca iz Laplaceove ali dvojne eksponentne porazdelitve z določeno lokacijo in merilom.
primer:
import numpy as np location, scale = 0., 2. s = np.random.laplace(location, scale, 10) s
Izhod:
array([-2.77127948, -1.46401453, -0.03723516, -1.61223942, 2.29590691, 1.74297722, 1.49438411, 0.30325513, -0.15948891, -4.99669747])
12) logistika ([lokacija, obseg, velikost])
Ta funkcija se uporablja za črpanje vzorca iz logistične distribucije.
primer:
import numpy as np import matplotlib.pyplot as plt location, scale = 10, 1 s1 = np.random.logistic(location, scale, 10000) count, bins, ignored = plt.hist(s1, bins=50) count bins ignored plt.show()
Izhod:
array([1.000e+00, 1.000e+00, 1.000e+00, 0.000e+00, 1.000e+00, 1.000e+00, 1.000e+00, 5.000e+00, 7.000e+00, 1.100e+01, 1.800e+01, 3.500e+01, 5.300e+01, 6.700e+01, 1.150e+02, 1.780e+02, 2.300e+02, 3.680e+02, 4.910e+02, 6.400e+02, 8.250e+02, 9.100e+02, 9.750e+02, 1.039e+03, 9.280e+02, 8.040e+02, 6.530e+02, 5.240e+02, 3.380e+02, 2.470e+02, 1.650e+02, 1.150e+02, 8.500e+01, 6.400e+01, 3.300e+01, 1.600e+01, 2.400e+01, 1.400e+01, 4.000e+00, 5.000e+00, 2.000e+00, 2.000e+00, 1.000e+00, 1.000e+00, 0.000e+00, 1.000e+00, 0.000e+00, 0.000e+00, 0.000e+00, 1.000e+00]) array([ 0.50643911, 0.91891814, 1.33139717, 1.7438762 , 2.15635523, 2.56883427, 2.9813133 , 3.39379233, 3.80627136, 4.2187504 , 4.63122943, 5.04370846, 5.45618749, 5.86866652, 6.28114556, 6.69362459, 7.10610362, 7.51858265, 7.93106169, 8.34354072, 8.75601975, 9.16849878, 9.58097781, 9.99345685, 10.40593588, 10.81841491, 11.23089394, 11.64337298, 12.05585201, 12.46833104, 12.88081007, 13.2932891 , 13.70576814, 14.11824717, 14.5307262 , 14.94320523, 15.35568427, 15.7681633 , 16.18064233, 16.59312136, 17.00560039, 17.41807943, 17.83055846, 18.24303749, 18.65551652, 19.06799556, 19.48047459, 19.89295362, 20.30543265, 20.71791168, 21.13039072]) <a 50 list of patch objects> </a>

13) lognormal([srednja vrednost, sigma, velikost])
Ta funkcija se uporablja za črpanje vzorca iz log-normalne porazdelitve.
primer:
import numpy as np mu, sigma = 2., 1. s1 = np.random.lognormal(mu, sigma, 1000) import matplotlib.pyplot as plt count, bins, ignored = plt.hist(s1, 100, density=True, ) a = np.linspace(min(bins), max(bins), 10000) pdf = (np.exp(-(np.log(a) - mu)**2 / (2 * sigma**2))/ (a * sigma * np.sqrt(2 * np.pi))) plt.plot(a, pdf, linewidth=2, color='r') plt.axis('tight') plt.show()
Izhod:

14) logseries(p[, velikost])
Ta funkcija se uporablja za črpanje vzorca iz logaritemske porazdelitve.
primer:
import numpy as np x = .6 s1 = np.random.logseries(x, 10000) count, bins, ignored = plt.hist(s1) def logseries(k, p): return -p**k/(k*log(1-p)) plt.plot(bins, logseries(bins, x)*count.max()/logseries(bins, a).max(), 'r') plt.show()
Izhod:

15) multinom (n, pvals [, velikost])
Ta funkcija se uporablja za risanje vzorca iz multinomske porazdelitve.
primer:
import numpy as np np.random.multinomial(20, [1/6.]*6, size=1)
Izhod:
array([[4, 2, 5, 5, 3, 1]])
16) multivariate_normal(mean, cov[, size, ...)
Ta funkcija se uporablja za črpanje vzorca iz večvariatne normalne porazdelitve.
primer:
import numpy as np mean = (1, 2) coveriance = [[1, 0], [0, 100]] import matplotlib.pyplot as plt a, b = np.random.multivariate_normal(mean, coveriance, 5000).T plt.plot(a, b, 'x') plt.axis('equal'023 030 ) plt.show()
Izhod:

17) negativni_binom (n, p[, velikost])
Ta funkcija se uporablja za črpanje vzorca iz negativne binomske porazdelitve.
primer:
import numpy as np s1 = np.random.negative_binomial(1, 0.1, 100000) for i in range(1, 11): probability = sum(s1 <i) 36 100000. print i, \'wells drilled, probability of one success=", probability </pre> <p> <strong>Output:</strong> </p> <pre> 1 wells drilled, probability of one success = 0 2 wells drilled, probability of one success = 0 3 wells drilled, probability of one success = 0 4 wells drilled, probability of one success = 0 5 wells drilled, probability of one success = 0 6 wells drilled, probability of one success = 0 7 wells drilled, probability of one success = 0 8 wells drilled, probability of one success = 0 9 wells drilled, probability of one success = 0 10 wells drilled, probability of one success = 0 </pre> <p > <strong>18) noncentral_chisquare(df, nonc[, size])</strong> </p> <p>This function is used to draw sample from a noncentral chi-square distribution. </p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt val = plt.hist(np.random.noncentral_chisquare(3, 25, 100000), bins=200, normed=True) plt.show() </pre> <p> <strong>Output:</strong> </p> <img src=" techcodeview.com img numpy-tutorial numpy-random-python-9.webp\' alt="numpy.random in Python"> <p> <strong>19) normal([loc, scale, size])</strong> </p> <p>This function is used to draw sample from a normal distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt mu, sigma = 0, 0.2 # mean and standard deviation s1 = np.random.normal(mu, sigma, 1000) abs(mu - np.mean(s1)) <0.01 1 abs(sigma - np.std(s1, ddof="1))" < 0.01 count, bins, ignored="plt.hist(s1," 30, density="True)" plt.plot(bins, (sigma * np.sqrt(2 np.pi)) *np.exp( (bins mu)**2 (2 sigma**2) ), linewidth="2," color="r" ) plt.show() pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-10.webp" alt="numpy.random in Python"> <p> <strong>20) pareto(a[, size])</strong> </p> <p>This function is used to draw samples from a Lomax or Pareto II with specified shape.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt b, m1 = 3., 2. # shape and mode s1 = (np.random.pareto(b, 1000) + 1) * m1 count, bins, _ = plt.hist(s1, 100, density=True) fit = b*m**b / bins**(b+1) plt.plot(bins, max(count)*fit/max(fit), linewidth=2, color='r') plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-11.webp" alt="numpy.random in Python"> <p> <strong>21) power(a[, size])</strong> </p> <p>This function is used to draw samples in [0, 1] from a power distribution with positive exponent a-1.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np x = 5. # shape samples = 1000 s1 = np.random.power(x, samples) import matplotlib.pyplot as plt count, bins, ignored = plt.hist(s1, bins=30) a = np.linspace(0, 1, 100) b = x*a**(x-1.) density_b = samples*np.diff(bins)[0]*b plt.plot(a, density_b) plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-12.webp" alt="numpy.random in Python"> <p> <strong>22) rayleigh([scale, size])</strong> </p> <p>This function is used to draw sample from a Rayleigh distribution.</p> <p> <strong>Example:</strong> </p> <pre> val = hist(np.random.rayleigh(3, 100000), bins=200, density=True) meanval = 1 modeval = np.sqrt(2 / np.pi) * meanval s1 = np.random.rayleigh(modeval, 1000000) 100.*sum(s1>3)/1000000. </pre> <p> <strong>Output:</strong> </p> <pre> 0.087300000000000003 </pre> <p><img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-13.webp" alt="numpy.random in Python"></p> <p> <strong>23) standard_cauchy([size])</strong> </p> <p>This function is used to draw sample from a standard Cauchy distribution with mode=0.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt s1 = np.random.standard_cauchy(1000000) s1 = s1[(s1>-25) & (s1<25)] # truncate distribution so it plots well plt.hist(s1, bins="100)" plt.show() < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-14.webp" alt="numpy.random in Python"> <p> <strong>24) standard_exponential([size])</strong> </p> <p>This function is used to draw sample from a standard exponential distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np n = np.random.standard_exponential((2, 7000)) </pre> <p> <strong>Output:</strong> </p> <pre> array([[0.53857931, 0.181262 , 0.20478701, ..., 3.66232881, 1.83882709, 1.77963295], [0.65163973, 1.40001955, 0.7525986 , ..., 0.76516523, 0.8400617 , 0.88551011]]) </pre> <p> <strong>25) standard_gamma([size])</strong> </p> <p>This function is used to draw sample from a standard Gamma distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np shape, scale = 2., 1. s1 = np.random.standard_gamma(shape, 1000000) import matplotlib.pyplot as plt import scipy.special as sps count1, bins1, ignored1 = plt.hist(s, 50, density=True) y = bins1**(shape-1) * ((np.exp(-bins1/scale))/ (sps.gamma(shape) * scale**shape)) plt.plot(bins1, y, linewidth=2, color='r') plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-15.webp" alt="numpy.random in Python"> <p> <strong>26) standard_normal([size])</strong> </p> <p>This function is used to draw sample from a standard Normal distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt s1= np.random.standard_normal(8000) s1 q = np.random.standard_normal(size=(3, 4, 2)) q </pre> <p> <strong>Output:</strong> </p> <pre> array([-3.14907597, 0.95366265, -1.20100026, ..., 3.47180222, 0.9608679 , 0.0774319 ]) array([[[ 1.55635461, -1.29541713], [-1.50534663, -0.02829194], [ 1.03949348, -0.26128132], [ 1.51921798, 0.82136178]], [[-0.4011052 , -0.52458858], [-1.31803814, 0.37415379], [-0.67077365, 0.97447018], [-0.20212115, 0.67840888]], [[ 1.86183474, 0.19946562], [-0.07376021, 0.84599701], [-0.84341386, 0.32081667], [-3.32016062, -1.19029818]]]) </pre> <p> <strong>27) standard_t(df[, size])</strong> </p> <p>This function is used to draw sample from a standard Student's distribution with df degree of freedom.</p> <p> <strong>Example:</strong> </p> <pre> intake = np.array([5260., 5470, 5640, 6180, 6390, 6515, 6805, 7515,8230,8770]) s1 = np.random.standard_t(10, size=100000) np.mean(intake) intake.std(ddof=1) t = (np.mean(intake)-7725)/(intake.std(ddof=1)/np.sqrt(len(intake))) h = plt.hist(s1, bins=100, density=True) np.sum(s1<t) float(len(s1)) plt.show() < pre> <p> <strong>Output:</strong> </p> <pre> 6677.5 1174.1101831694598 0.00864 </pre> <p><img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-16.webp" alt="numpy.random in Python"></p> <p> <strong>28) triangular(left, mode, right[, size])</strong> </p> <p>This function is used to draw sample from a triangular distribution over the interval.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt h = plt.hist(np.random.triangular(-4, 0, 8, 1000000), bins=300,density=True) plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-17.webp" alt="numpy.random in Python"> <p> <strong>29) uniform([low, high, size])</strong> </p> <p>This function is used to draw sample from a uniform distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt s1 = np.random.uniform(-1,0,1000) np.all(s1 >= -1) np.all(s1 <0) count, bins, ignored="plt.hist(s1," 15, density="True)" plt.plot(bins, np.ones_like(bins), linewidth="2," color="r" ) plt.show() < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-18.webp" alt="numpy.random in Python"> <p> <strong>30) vonmises(m1, m2[, size])</strong> </p> <p>This function is used to draw sample from a von Mises distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt m1, m2 = 0.0, 4.0 s1 = np.random.vonmises(m1, m2, 1000) from scipy.special import i0 plt.hist(s1, 50, density=True) x = np.linspace(-np.pi, np.pi, num=51) y = np.exp(m2*np.cos(x-m1))/(2*np.pi*i0(m2)) plt.plot(x, y, linewidth=2, color='r') plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-19.webp" alt="numpy.random in Python"> <p> <strong>31) wald(mean, scale[, size])</strong> </p> <p>This function is used to draw sample from a Wald, or inverse Gaussian distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt h = plt.hist(np.random.wald(3, 3, 100000), bins=250, density=True) plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-20.webp" alt="numpy.random in Python"> <p> <strong>32) weibull(a[, size])</strong> </p> <p>This function is used to draw sample from a Weibull distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt from scipy import special x=2.0 s=np.random.weibull(x, 1000) a = np.arange(1, 100.)/50. def weib(x, n, a): return (a/n)*(x/n)**np.exp(-(x/n)**a) count, bins, ignored = plt.hist(np.random.weibull(5.,1000)) a= np.arange(1,100.)/50. scale = count.max()/weib(x, 1., 5.).max() scale = count.max()/weib(a, 1., 5.).max() plt.plot(x, weib(x, 1., 5.)*scale) plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-21.webp" alt="numpy.random in Python"> <p> <strong>33) zipf(a[, size])</strong> </p> <p>This function is used to draw sample from a Zipf distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt from scipy import special x=2.0 s=np.random.zipf(x, 1000) count, bins, ignored = plt.hist(s[s<50], 50, density="True)" a="np.arange(1.," 50.) b="a**(-x)" special.zetac(x) plt.plot(a, max(b), linewidth="2," color="r" ) plt.show() < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-22.webp" alt="numpy.random in Python"> <hr></50],></pre></0)></pre></t)></pre></25)]></pre></0.01></pre></i)>
Izhod:

21) moč (a[, velikost])
Ta funkcija se uporablja za črpanje vzorcev v [0, 1] iz porazdelitve moči s pozitivnim eksponentom a-1.
primer:
import numpy as np x = 5. # shape samples = 1000 s1 = np.random.power(x, samples) import matplotlib.pyplot as plt count, bins, ignored = plt.hist(s1, bins=30) a = np.linspace(0, 1, 100) b = x*a**(x-1.) density_b = samples*np.diff(bins)[0]*b plt.plot(a, density_b) plt.show()
Izhod:

22) rayleigh([merilo, velikost])
Ta funkcija se uporablja za črpanje vzorca iz Rayleighove porazdelitve.
primer:
val = hist(np.random.rayleigh(3, 100000), bins=200, density=True) meanval = 1 modeval = np.sqrt(2 / np.pi) * meanval s1 = np.random.rayleigh(modeval, 1000000) 100.*sum(s1>3)/1000000.
Izhod:
0.087300000000000003

23) standard_cauchy([velikost])
Ta funkcija se uporablja za črpanje vzorca iz standardne Cauchyjeve porazdelitve z načinom=0.
primer:
import numpy as np import matplotlib.pyplot as plt s1 = np.random.standard_cauchy(1000000) s1 = s1[(s1>-25) & (s1<25)] # truncate distribution so it plots well plt.hist(s1, bins="100)" plt.show() < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-14.webp" alt="numpy.random in Python"> <p> <strong>24) standard_exponential([size])</strong> </p> <p>This function is used to draw sample from a standard exponential distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np n = np.random.standard_exponential((2, 7000)) </pre> <p> <strong>Output:</strong> </p> <pre> array([[0.53857931, 0.181262 , 0.20478701, ..., 3.66232881, 1.83882709, 1.77963295], [0.65163973, 1.40001955, 0.7525986 , ..., 0.76516523, 0.8400617 , 0.88551011]]) </pre> <p> <strong>25) standard_gamma([size])</strong> </p> <p>This function is used to draw sample from a standard Gamma distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np shape, scale = 2., 1. s1 = np.random.standard_gamma(shape, 1000000) import matplotlib.pyplot as plt import scipy.special as sps count1, bins1, ignored1 = plt.hist(s, 50, density=True) y = bins1**(shape-1) * ((np.exp(-bins1/scale))/ (sps.gamma(shape) * scale**shape)) plt.plot(bins1, y, linewidth=2, color='r') plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-15.webp" alt="numpy.random in Python"> <p> <strong>26) standard_normal([size])</strong> </p> <p>This function is used to draw sample from a standard Normal distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt s1= np.random.standard_normal(8000) s1 q = np.random.standard_normal(size=(3, 4, 2)) q </pre> <p> <strong>Output:</strong> </p> <pre> array([-3.14907597, 0.95366265, -1.20100026, ..., 3.47180222, 0.9608679 , 0.0774319 ]) array([[[ 1.55635461, -1.29541713], [-1.50534663, -0.02829194], [ 1.03949348, -0.26128132], [ 1.51921798, 0.82136178]], [[-0.4011052 , -0.52458858], [-1.31803814, 0.37415379], [-0.67077365, 0.97447018], [-0.20212115, 0.67840888]], [[ 1.86183474, 0.19946562], [-0.07376021, 0.84599701], [-0.84341386, 0.32081667], [-3.32016062, -1.19029818]]]) </pre> <p> <strong>27) standard_t(df[, size])</strong> </p> <p>This function is used to draw sample from a standard Student's distribution with df degree of freedom.</p> <p> <strong>Example:</strong> </p> <pre> intake = np.array([5260., 5470, 5640, 6180, 6390, 6515, 6805, 7515,8230,8770]) s1 = np.random.standard_t(10, size=100000) np.mean(intake) intake.std(ddof=1) t = (np.mean(intake)-7725)/(intake.std(ddof=1)/np.sqrt(len(intake))) h = plt.hist(s1, bins=100, density=True) np.sum(s1<t) float(len(s1)) plt.show() < pre> <p> <strong>Output:</strong> </p> <pre> 6677.5 1174.1101831694598 0.00864 </pre> <p><img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-16.webp" alt="numpy.random in Python"></p> <p> <strong>28) triangular(left, mode, right[, size])</strong> </p> <p>This function is used to draw sample from a triangular distribution over the interval.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt h = plt.hist(np.random.triangular(-4, 0, 8, 1000000), bins=300,density=True) plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-17.webp" alt="numpy.random in Python"> <p> <strong>29) uniform([low, high, size])</strong> </p> <p>This function is used to draw sample from a uniform distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt s1 = np.random.uniform(-1,0,1000) np.all(s1 >= -1) np.all(s1 <0) count, bins, ignored="plt.hist(s1," 15, density="True)" plt.plot(bins, np.ones_like(bins), linewidth="2," color="r" ) plt.show() < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-18.webp" alt="numpy.random in Python"> <p> <strong>30) vonmises(m1, m2[, size])</strong> </p> <p>This function is used to draw sample from a von Mises distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt m1, m2 = 0.0, 4.0 s1 = np.random.vonmises(m1, m2, 1000) from scipy.special import i0 plt.hist(s1, 50, density=True) x = np.linspace(-np.pi, np.pi, num=51) y = np.exp(m2*np.cos(x-m1))/(2*np.pi*i0(m2)) plt.plot(x, y, linewidth=2, color='r') plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-19.webp" alt="numpy.random in Python"> <p> <strong>31) wald(mean, scale[, size])</strong> </p> <p>This function is used to draw sample from a Wald, or inverse Gaussian distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt h = plt.hist(np.random.wald(3, 3, 100000), bins=250, density=True) plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-20.webp" alt="numpy.random in Python"> <p> <strong>32) weibull(a[, size])</strong> </p> <p>This function is used to draw sample from a Weibull distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt from scipy import special x=2.0 s=np.random.weibull(x, 1000) a = np.arange(1, 100.)/50. def weib(x, n, a): return (a/n)*(x/n)**np.exp(-(x/n)**a) count, bins, ignored = plt.hist(np.random.weibull(5.,1000)) a= np.arange(1,100.)/50. scale = count.max()/weib(x, 1., 5.).max() scale = count.max()/weib(a, 1., 5.).max() plt.plot(x, weib(x, 1., 5.)*scale) plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-21.webp" alt="numpy.random in Python"> <p> <strong>33) zipf(a[, size])</strong> </p> <p>This function is used to draw sample from a Zipf distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt from scipy import special x=2.0 s=np.random.zipf(x, 1000) count, bins, ignored = plt.hist(s[s<50], 50, density="True)" a="np.arange(1.," 50.) b="a**(-x)" special.zetac(x) plt.plot(a, max(b), linewidth="2," color="r" ) plt.show() < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-22.webp" alt="numpy.random in Python"> <hr></50],></pre></0)></pre></t)></pre></25)]>
Izhod:
array([[0.53857931, 0.181262 , 0.20478701, ..., 3.66232881, 1.83882709, 1.77963295], [0.65163973, 1.40001955, 0.7525986 , ..., 0.76516523, 0.8400617 , 0.88551011]])
25) standardna_gama([velikost])
Ta funkcija se uporablja za črpanje vzorca iz standardne porazdelitve gama.
primer:
import numpy as np shape, scale = 2., 1. s1 = np.random.standard_gamma(shape, 1000000) import matplotlib.pyplot as plt import scipy.special as sps count1, bins1, ignored1 = plt.hist(s, 50, density=True) y = bins1**(shape-1) * ((np.exp(-bins1/scale))/ (sps.gamma(shape) * scale**shape)) plt.plot(bins1, y, linewidth=2, color='r') plt.show()
Izhod:

26) standard_normal([velikost])
Ta funkcija se uporablja za črpanje vzorca iz standardne normalne porazdelitve.
primer:
import numpy as np import matplotlib.pyplot as plt s1= np.random.standard_normal(8000) s1 q = np.random.standard_normal(size=(3, 4, 2)) q
Izhod:
array([-3.14907597, 0.95366265, -1.20100026, ..., 3.47180222, 0.9608679 , 0.0774319 ]) array([[[ 1.55635461, -1.29541713], [-1.50534663, -0.02829194], [ 1.03949348, -0.26128132], [ 1.51921798, 0.82136178]], [[-0.4011052 , -0.52458858], [-1.31803814, 0.37415379], [-0.67077365, 0.97447018], [-0.20212115, 0.67840888]], [[ 1.86183474, 0.19946562], [-0.07376021, 0.84599701], [-0.84341386, 0.32081667], [-3.32016062, -1.19029818]]])
27) standard_t(df[, velikost])
Ta funkcija se uporablja za črpanje vzorca iz standardne Studentove porazdelitve s prostostno stopnjo df.
kako najti skrite stvari na androidu
primer:
intake = np.array([5260., 5470, 5640, 6180, 6390, 6515, 6805, 7515,8230,8770]) s1 = np.random.standard_t(10, size=100000) np.mean(intake) intake.std(ddof=1) t = (np.mean(intake)-7725)/(intake.std(ddof=1)/np.sqrt(len(intake))) h = plt.hist(s1, bins=100, density=True) np.sum(s1<t) float(len(s1)) plt.show() < pre> <p> <strong>Output:</strong> </p> <pre> 6677.5 1174.1101831694598 0.00864 </pre> <p><img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-16.webp" alt="numpy.random in Python"></p> <p> <strong>28) triangular(left, mode, right[, size])</strong> </p> <p>This function is used to draw sample from a triangular distribution over the interval.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt h = plt.hist(np.random.triangular(-4, 0, 8, 1000000), bins=300,density=True) plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-17.webp" alt="numpy.random in Python"> <p> <strong>29) uniform([low, high, size])</strong> </p> <p>This function is used to draw sample from a uniform distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt s1 = np.random.uniform(-1,0,1000) np.all(s1 >= -1) np.all(s1 <0) count, bins, ignored="plt.hist(s1," 15, density="True)" plt.plot(bins, np.ones_like(bins), linewidth="2," color="r" ) plt.show() < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-18.webp" alt="numpy.random in Python"> <p> <strong>30) vonmises(m1, m2[, size])</strong> </p> <p>This function is used to draw sample from a von Mises distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt m1, m2 = 0.0, 4.0 s1 = np.random.vonmises(m1, m2, 1000) from scipy.special import i0 plt.hist(s1, 50, density=True) x = np.linspace(-np.pi, np.pi, num=51) y = np.exp(m2*np.cos(x-m1))/(2*np.pi*i0(m2)) plt.plot(x, y, linewidth=2, color='r') plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-19.webp" alt="numpy.random in Python"> <p> <strong>31) wald(mean, scale[, size])</strong> </p> <p>This function is used to draw sample from a Wald, or inverse Gaussian distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt h = plt.hist(np.random.wald(3, 3, 100000), bins=250, density=True) plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-20.webp" alt="numpy.random in Python"> <p> <strong>32) weibull(a[, size])</strong> </p> <p>This function is used to draw sample from a Weibull distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt from scipy import special x=2.0 s=np.random.weibull(x, 1000) a = np.arange(1, 100.)/50. def weib(x, n, a): return (a/n)*(x/n)**np.exp(-(x/n)**a) count, bins, ignored = plt.hist(np.random.weibull(5.,1000)) a= np.arange(1,100.)/50. scale = count.max()/weib(x, 1., 5.).max() scale = count.max()/weib(a, 1., 5.).max() plt.plot(x, weib(x, 1., 5.)*scale) plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-21.webp" alt="numpy.random in Python"> <p> <strong>33) zipf(a[, size])</strong> </p> <p>This function is used to draw sample from a Zipf distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt from scipy import special x=2.0 s=np.random.zipf(x, 1000) count, bins, ignored = plt.hist(s[s<50], 50, density="True)" a="np.arange(1.," 50.) b="a**(-x)" special.zetac(x) plt.plot(a, max(b), linewidth="2," color="r" ) plt.show() < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-22.webp" alt="numpy.random in Python"> <hr></50],></pre></0)></pre></t)>

28) trikotno (levo, način, desno [, velikost])
Ta funkcija se uporablja za risanje vzorca iz trikotne porazdelitve v intervalu.
primer:
import numpy as np import matplotlib.pyplot as plt h = plt.hist(np.random.triangular(-4, 0, 8, 1000000), bins=300,density=True) plt.show()
Izhod:

29) uniforma([nizka, visoka, velikost])
Ta funkcija se uporablja za črpanje vzorca iz enotne porazdelitve.
primer:
import numpy as np import matplotlib.pyplot as plt s1 = np.random.uniform(-1,0,1000) np.all(s1 >= -1) np.all(s1 <0) count, bins, ignored="plt.hist(s1," 15, density="True)" plt.plot(bins, np.ones_like(bins), linewidth="2," color="r" ) plt.show() < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-18.webp" alt="numpy.random in Python"> <p> <strong>30) vonmises(m1, m2[, size])</strong> </p> <p>This function is used to draw sample from a von Mises distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt m1, m2 = 0.0, 4.0 s1 = np.random.vonmises(m1, m2, 1000) from scipy.special import i0 plt.hist(s1, 50, density=True) x = np.linspace(-np.pi, np.pi, num=51) y = np.exp(m2*np.cos(x-m1))/(2*np.pi*i0(m2)) plt.plot(x, y, linewidth=2, color='r') plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-19.webp" alt="numpy.random in Python"> <p> <strong>31) wald(mean, scale[, size])</strong> </p> <p>This function is used to draw sample from a Wald, or inverse Gaussian distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt h = plt.hist(np.random.wald(3, 3, 100000), bins=250, density=True) plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-20.webp" alt="numpy.random in Python"> <p> <strong>32) weibull(a[, size])</strong> </p> <p>This function is used to draw sample from a Weibull distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt from scipy import special x=2.0 s=np.random.weibull(x, 1000) a = np.arange(1, 100.)/50. def weib(x, n, a): return (a/n)*(x/n)**np.exp(-(x/n)**a) count, bins, ignored = plt.hist(np.random.weibull(5.,1000)) a= np.arange(1,100.)/50. scale = count.max()/weib(x, 1., 5.).max() scale = count.max()/weib(a, 1., 5.).max() plt.plot(x, weib(x, 1., 5.)*scale) plt.show() </pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-21.webp" alt="numpy.random in Python"> <p> <strong>33) zipf(a[, size])</strong> </p> <p>This function is used to draw sample from a Zipf distribution.</p> <p> <strong>Example:</strong> </p> <pre> import numpy as np import matplotlib.pyplot as plt from scipy import special x=2.0 s=np.random.zipf(x, 1000) count, bins, ignored = plt.hist(s[s<50], 50, density="True)" a="np.arange(1.," 50.) b="a**(-x)" special.zetac(x) plt.plot(a, max(b), linewidth="2," color="r" ) plt.show() < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-22.webp" alt="numpy.random in Python"> <hr></50],></pre></0)>
Izhod:

31) wald(povprečje, lestvica[, velikost])
Ta funkcija se uporablja za črpanje vzorca iz Waldove ali inverzne Gaussove porazdelitve.
primer:
import numpy as np import matplotlib.pyplot as plt h = plt.hist(np.random.wald(3, 3, 100000), bins=250, density=True) plt.show()
Izhod:

32) weibull(a[, velikost])
Ta funkcija se uporablja za črpanje vzorca iz Weibullove porazdelitve.
primer:
import numpy as np import matplotlib.pyplot as plt from scipy import special x=2.0 s=np.random.weibull(x, 1000) a = np.arange(1, 100.)/50. def weib(x, n, a): return (a/n)*(x/n)**np.exp(-(x/n)**a) count, bins, ignored = plt.hist(np.random.weibull(5.,1000)) a= np.arange(1,100.)/50. scale = count.max()/weib(x, 1., 5.).max() scale = count.max()/weib(a, 1., 5.).max() plt.plot(x, weib(x, 1., 5.)*scale) plt.show()
Izhod:

33) zipf(a[, velikost])
Ta funkcija se uporablja za črpanje vzorca iz distribucije Zipf.
primer:
import numpy as np import matplotlib.pyplot as plt from scipy import special x=2.0 s=np.random.zipf(x, 1000) count, bins, ignored = plt.hist(s[s<50], 50, density="True)" a="np.arange(1.," 50.) b="a**(-x)" special.zetac(x) plt.plot(a, max(b), linewidth="2," color="r" ) plt.show() < pre> <p> <strong>Output:</strong> </p> <img src="//techcodeview.com/img/numpy-tutorial/36/numpy-random-python-22.webp" alt="numpy.random in Python"> <hr></50],>
