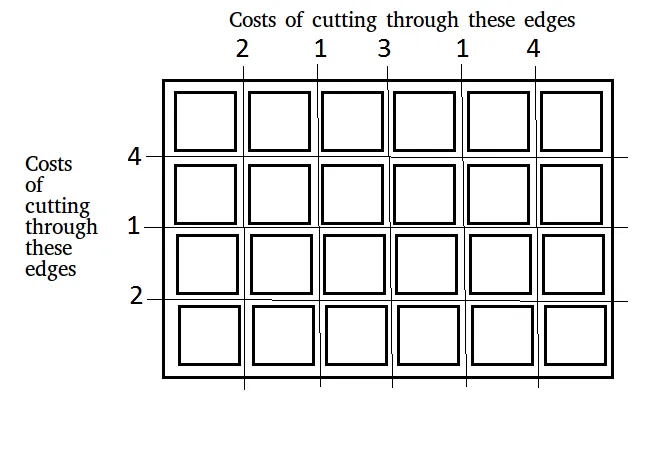
Glede na ploščo dimenzij n × m ki ga je treba razrezati na n × m kvadratov. Stroški reza vzdolž vodoravnega ali navpičnega roba so navedeni v dveh nizih:

• x[] : Zniževanje stroškov vzdolž navpičnih robov (po dolžini).
• in [] : Zniževanje stroškov vzdolž vodoravnih robov (po širini).

Poiščite minimalne skupne stroške, potrebne za optimalno rezanje deske na kvadrate.

Primeri: 

Vnos: x[] = [2 1 3 1 4] y[] = [4 1 2] n = 4 m = 6
Izhod: 42
Pojasnilo:

Sprva št. vodoravnih segmentov = 1 & št. navpičnih segmentov = 1.
Optimalen način rezanja na kvadrat je:
Izberite 4 (od x) -> navpični rez Cena = 4 × vodoravni segmenti = 4
 Zdaj vodoravni segmenti = 1 navpični segmenti = 2.
Izberite 4 (od y) -> vodoravni rez Cena = 4 × navpični segmenti = 8
 Sedaj vodoravni segmenti = 2 navpični segmenti = 2.
Izberite 3 (od x) -> navpični rez Cena = 3 × vodoravni segmenti = 6
 Sedaj vodoravni segmenti = 2 navpični segmenti = 3.
Izberi 2 (od x) -> navpični rez Cena = 2 × vodoravni segmenti = 4
 Sedaj vodoravni segmenti = 2 navpični segmenti = 4.
Izberite 2 (od y) -> vodoravni rez Cena = 2 × navpični segmenti = 8
 Zdaj vodoravni segmenti = 3 navpični segmenti = 4.
Izberi 1 (od x) -> navpični rez Cena = 1 × vodoravni segmenti = 3
Sedaj vodoravni segmenti = 3 navpični segmenti = 5.
Izberi 1 (od x) -> navpični rez Cena = 1 × vodoravni segmenti = 3
Zdaj vodoravni segmenti = 3 navpični segmenti = 6.
Izberi 1 (od y) -> vodoravni rez Cena = 1 × navpični segmenti = 6
Zdaj vodoravni segmenti = 4 navpični segmenti = 6.
Torej skupni strošek = 4 + 8 + 6 + 4 + 8 + 3 + 3 + 6 = 42.

Vnos: x[] = [1 1 1] y[] = [1 1 1] n = 4 m = 4
Izhod: 15
Pojasnilo:
Sprva št. vodoravnih segmentov = 1 & št. navpičnih segmentov = 1.
Optimalen način rezanja na kvadrat je:
Izberite 1 (od y) -> vodoravni rez Cena = 1 × navpični segmenti = 1
Sedaj vodoravni segmenti = 2 navpični segmenti = 1.
Izberite 1 (od y) -> vodoravni rez Cena = 1 × navpični segmenti = 1
Zdaj vodoravni segmenti = 3 navpični segmenti = 1.
Izberite 1 (od y) -> vodoravni rez Cena = 1 × navpični segmenti = 1
Zdaj vodoravni segmenti = 4 navpični segmenti = 1.
Izberi 1 (od x) -> navpični rez Cena = 1 × vodoravni segmenti = 4
Zdaj vodoravni segmenti = 4 navpični segmenti = 2.
Izberi 1 (od x) -> navpični rez Cena = 1 × vodoravni segmenti = 4
Zdaj vodoravni segmenti = 4 navpični segmenti = 3.
Izberi 1 (od x) -> navpični rez Cena = 1 × vodoravni segmenti = 4
Zdaj vodoravni segmenti = 4 navpični segmenti = 4
Torej skupni strošek = 1 + 1 + 1 + 4 + 4 + 4 = 15.

Kazalo vsebine

• [Naivni pristop] Preizkusite vse permutacije - O((n+m)!×(n+m)) čas in O(n+m) prostor
• [Pričakovani pristop] Uporaba pohlepne tehnike - O( n (log n)+m (log m)) čas in O(1) prostor

[Naivni pristop] Preizkusite vse permutacije - O((n+m)!×(n+m)) čas in O(n+m) prostor

Ideja je ustvariti vse možne permutacije danih kosov in nato izračunati stroške za vsako permutacijo. Končno med njimi vrnite minimalne stroške.

Opomba: Ta pristop ni izvedljiv za večje vložke, ker število permutacij faktorsko raste kot (m+n-2)!.
Za vsako permutacijo moramo izračunati stroške v O(m+n) času. Zato celotna časovna kompleksnost postane O((m+n−2)!×(m+n)).

[Pričakovani pristop] Uporaba pohlepne tehnike - O( n (log n)+m (log m)) čas in O(1) prostor

Ideja je, da najprej naredite najdražje kose z uporabo a pohlepen pristop . Opažamo, da izbira najvišjega znižanja stroškov na vsakem koraku zmanjša prihodnje stroške, saj vpliva na več kosov hkrati. Stroške navpičnega (x) in vodoravnega (y) zmanjšanja razvrstimo v padajočem vrstnem redu, nato pa iterativno izberemo večjega, da povečamo prihranke stroškov. Preostali kosi se obdelajo ločeno, da se zagotovi optimalno razdelitev vseh delov.

Kaj se zgodi, ko naredimo rez?

• Horizontalni rez → režete po širini, tako da se poveča število vodoravnih trakov (hCount++). Toda strošek se pomnoži z vCount (število navpičnih trakov), ker mora vodoravni rez potekati skozi vse navpične segmente.
• Vertikalni rez → režete po višini, tako da se poveča število navpičnih trakov (vCount++). Toda strošek se pomnoži s hCount (število vodoravnih trakov), ker mora navpični rez potekati skozi vse vodoravne segmente.

Koraki za rešitev težave:

• Razvrsti matri x in y v padajočem vrstnem redu.
• Uporabite dva kazalca, enega za x in enega za y, začenši od največje vrednosti in se pomaknite proti manjšim vrednostim.
• Vzdržujte hCount in vCount za sledenje, na koliko segmentov vpliva vsak rez, in jih ustrezno posodobite.
• Ponavljajte medtem ko imata oba x in y neobdelane kose, pri čemer vedno izberete večjo stroškovo, da zmanjšate skupne stroške.
• Če x ima preostale reze, jih obdelajte z množiteljem hCount; podobno obdelajte preostale y reze z vCount.
• Zberite skupne stroške v vsakem koraku z uporabo formule: znižajte stroške * število prizadetih kosov, kar zagotavlja minimalne stroške.

#include   #include #include   using namespace std; int minCost(int n int m   vector<int>& x vector<int>& y) {    // Sort the cutting costs in ascending order  sort(x.begin() x.end());  sort(y.begin() y.end());   int hCount = 1 vCount = 1;   int i = x.size() - 1 j = y.size() - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } int main() {    int n = 4 m = 6;  vector<int> x = {2 1 3 1 4};  vector<int> y = {4 1 2};  cout << minCost(n m x y) << endl;  return 0; } 

import java.util.Arrays; class GfG {    static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Arrays.sort(x);  Arrays.sort(y);   int hCount = 1 vCount = 1;   int i = x.length - 1 j = y.length - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }  public static void main(String[] args) {    int n = 4m = 6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  System.out.println(minCost(n m x y));  } } 

def minCost(nm x y): # Sort the cutting costs in ascending order x.sort() y.sort() hCount vCount = 1 1 i j = len(x) - 1 len(y) - 1 totalCost = 0 while i >= 0 and j >= 0: # Choose the larger cost cut to  # minimize future costs if x[i] >= y[j]: totalCost += x[i] * hCount vCount += 1 i -= 1 else: totalCost += y[j] * vCount hCount += 1 j -= 1 # Process remaining vertical cuts while i >= 0: totalCost += x[i] * hCount vCount += 1 i -= 1 # Process remaining horizontal cuts while j >= 0: totalCost += y[j] * vCount hCount += 1 j -= 1 return totalCost if __name__ == '__main__': nm = 4 6 x = [2 1 3 1 4] y = [4 1 2] print(minCost(nmx y)) 

using System; class GfG {  public static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Array.Sort(x);  Array.Sort(y);  int hCount = 1 vCount = 1;  int i = x.Length - 1 j = y.Length - 1;  int totalCost = 0;  // Process the cuts in greedy manner  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }    public static void Main() {    int n=4m=6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  Console.WriteLine(minCost(nm x y));  } } 

function minCost( nm x y) {    // Sort the cutting costs in ascending order  x.sort((a b) => a - b);  y.sort((a b) => a - b);  let hCount = 1 vCount = 1;  let i = x.length - 1 j = y.length - 1;  let totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }   else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } // Driver Code let n = 4m = 6; let x = [2 1 3 1 4]; let y = [4 1 2]; console.log(minCost(nm x y)); 

42