Kaj je najnižji skupni prednik v binarnem drevesu?
The najnižji skupni prednik je najnižje vozlišče v drevesu, ki ima n1 in n2 kot potomci, kjer sta n1 in n2 vozlišči, za katera želimo najti LCA. Zato je LCA binarnega drevesa z vozliščema n1 in n2 skupni prednik n1 in n2, ki je najbolj oddaljen od korena.
Uporaba najnižjega skupnega prednika (LCA):
Če želite določiti razdaljo med pari vozlišč v drevesu: razdaljo od n1 do n2 lahko izračunate kot razdaljo od korena do n1 plus razdaljo od korena do n2, minus dvakratno razdaljo od korena do njune najnižje skupne točke. prednik.
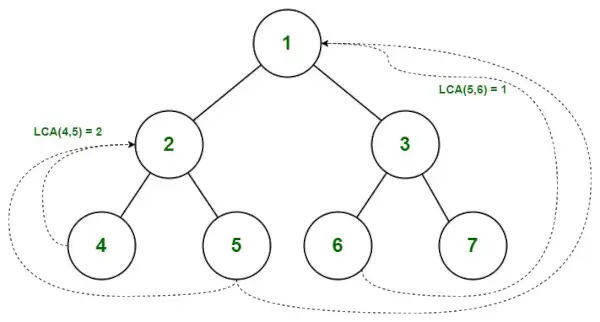
Najnižji skupni prednik v binarnem drevesu
Priporočena praksa Najnižji skupni prednik v binarnem drevesu Poskusite!
Najnižji skupni prednik v binarnem drevesu s shranjevanjem poti od korena do n1 in korena do n2:
Ideja tega pristopa je shraniti pot od korena do n1 in korena do n2 v dveh ločenih podatkovnih strukturah. Nato hkrati poglejte vrednosti, shranjene v podatkovni strukturi, in poiščite prvo neujemanje.
Ilustracija:
Poiščite LCA za 5 in 6
Pot od korena do 5 = { 1, 2, 5 }
Pot od korena do 6 = { 1, 3, 6 }
- Preverjanje začnemo od 0 indeksa. Ker se obe vrednosti ujemata (potA[0] = potB[0]), se premaknemo na naslednji indeks.
- potA[1] ni enaka potiB[1], obstaja neujemanje, zato upoštevamo prejšnjo vrednost.
- Zato je LCA za (5,6) = 1
Za rešitev težave sledite spodnjim korakom:
- Poiščite pot od korena do n1 in jo shranite v vektor ali polje.
- Poiščite pot od korena do n2 in jo shranite v drug vektor ali polje.
- Prečkajte obe poti, dokler vrednosti v nizih niso enake. Vrni skupni element tik pred neujemanjem.
Sledi izvedba zgornjega algoritma:
C++
// C++ Program for Lowest Common Ancestor> // in a Binary Tree> // A O(n) solution to find LCA> // of two given values n1 and n2> #include> using> namespace> std;> // A Binary Tree node> struct> Node {> >int> key;> >struct> Node *left, *right;> };> // Utility function creates a new binary tree node with> // given key> Node* newNode(>int> k)> {> >Node* temp =>new> Node;> >temp->ključ = k;> >temp->levo = temp->desno = NULL;> >return> temp;> }> // Finds the path from root node to given root of the tree,> // Stores the path in a vector path[], returns true if path> // exists otherwise false> bool> findPath(Node* root, vector<>int>>& pot,>int> k)> (root->desno && findPath(root->right, path, k)))> >return> true>;> >// If not present in subtree rooted with root, remove> >// root from path[] and return false> >path.pop_back();> >return> false>;> > // Returns LCA if node n1, n2 are present in the given> // binary tree, otherwise return -1> int> findLCA(Node* root,>int> n1,>int> n2)> > // Driver program to test above functions> int> main()> {> >// Let us create the Binary Tree shown in above diagram.> >Node* root = newNode(1);> >root->levo = novoVozlišče(2);> >root->desno = novoVozlišče(3);> >root->levo->levo = novoVozlišče(4);> >root->levo->desno = novoVozlišče(5);> >root->desno->levo = novoVozlišče(6);>> >root->desno->desno = novoVozlišče(7);> >cout <<>'LCA(4, 5) = '> << findLCA(root, 4, 5);> >cout <<>'
LCA(4, 6) = '> << findLCA(root, 4, 6);> >cout <<>'
LCA(3, 4) = '> << findLCA(root, 3, 4);> >cout <<>'
LCA(2, 4) = '> << findLCA(root, 2, 4);> >return> 0;> }> |
>
>
Java
// Java Program for Lowest Common Ancestor> // in a Binary Tree> // A O(n) solution to find LCA of> // two given values n1 and n2> import> java.util.ArrayList;> import> java.util.List;> // A Binary Tree node> class> Node {> >int> data;> >Node left, right;> >Node(>int> value)> >{> >data = value;> >left = right =>null>;> >}> }> public> class> BT_NoParentPtr_Solution1 {> >Node root;> >private> List path1 =>new> ArrayList();> >private> List path2 =>new> ArrayList();> >// Finds the path from root node to given root of the> >// tree.> >int> findLCA(>int> n1,>int> n2)> >{> >path1.clear();> >path2.clear();> >return> findLCAInternal(root, n1, n2);> >}> >private> int> findLCAInternal(Node root,>int> n1,>int> n2)> >{> >if> (!findPath(root, n1, path1)> >|| !findPath(root, n2, path2)) {> >System.out.println((path1.size()>>0>)> >?>'n1 is present'> >:>'n1 is missing'>);> >System.out.println((path2.size()>>0>)> >?>'n2 is present'> >:>'n2 is missing'>);> >return> ->1>;> >}> >int> i;> >for> (i =>0>; i i++) { // System.out.println(path1.get(i) + ' ' + // path2.get(i)); if (!path1.get(i).equals(path2.get(i))) break; } return path1.get(i - 1); } // Finds the path from root node to given root of the // tree, Stores the path in a vector path[], returns // true if path exists otherwise false private boolean findPath(Node root, int n, List path) { // base case if (root == null) { return false; } // Store this node . The node will be removed if // not in path from root to n. path.add(root.data); if (root.data == n || findPath(root.left, n, path) || findPath(root.right, n, path)) { return true; } // If not present in subtree rooted with root, // remove root from path[] and return false path.remove(path.size() - 1); return false; } // Driver code public static void main(String[] args) { BT_NoParentPtr_Solution1 tree = new BT_NoParentPtr_Solution1(); tree.root = new Node(1); tree.root.left = new Node(2); tree.root.right = new Node(3); tree.root.left.left = new Node(4); tree.root.left.right = new Node(5); tree.root.right.left = new Node(6); tree.root.right.right = new Node(7); System.out.println('LCA(4, 5) = ' + tree.findLCA(4, 5)); System.out.println('LCA(4, 6) = ' + tree.findLCA(4, 6)); System.out.println('LCA(3, 4) = ' + tree.findLCA(3, 4)); System.out.println('LCA(2, 4) = ' + tree.findLCA(2, 4)); } } // This code is contributed by Sreenivasulu Rayanki.> |
>
>
Python3
# Python Program for Lowest Common Ancestor in a Binary Tree> # O(n) solution to find LCS of two given values n1 and n2> # A binary tree node> class> Node:> ># Constructor to create a new binary node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # Finds the path from root node to given root of the tree.> # Stores the path in a list path[], returns true if path> # exists otherwise false> def> findPath(root, path, k):> ># Baes Case> >if> root>is> None>:> >return> False> ># Store this node is path vector. The node will be> ># removed if not in path from root to k> >path.append(root.key)> ># See if the k is same as root's key> >if> root.key>=>=> k:> >return> True> ># Check if k is found in left or right sub-tree> >if> ((root.left !>=> None> and> findPath(root.left, path, k))>or> >(root.right !>=> None> and> findPath(root.right, path, k))):> >return> True> ># If not present in subtree rooted with root, remove> ># root from path and return False> >path.pop()> >return> False> # Returns LCA if node n1 , n2 are present in the given> # binary tree otherwise return -1> def> findLCA(root, n1, n2):> ># To store paths to n1 and n2 fromthe root> >path1>=> []> >path2>=> []> ># Find paths from root to n1 and root to n2.> ># If either n1 or n2 is not present , return -1> >if> (>not> findPath(root, path1, n1)>or> not> findPath(root, path2, n2)):> >return> ->1> ># Compare the paths to get the first different value> >i>=> 0> >while>(i <>len>(path1)>and> i <>len>(path2)):> >if> path1[i] !>=> path2[i]:> >break> >i>+>=> 1> >return> path1[i>->1>]> # Driver program to test above function> if> __name__>=>=> '__main__'>:> > ># Let's create the Binary Tree shown in above diagram> >root>=> Node(>1>)> >root.left>=> Node(>2>)> >root.right>=> Node(>3>)> >root.left.left>=> Node(>4>)> >root.left.right>=> Node(>5>)> >root.right.left>=> Node(>6>)> >root.right.right>=> Node(>7>)> > >print>(>'LCA(4, 5) = %d'> %> (findLCA(root,>4>,>5>,)))> >print>(>'LCA(4, 6) = %d'> %> (findLCA(root,>4>,>6>)))> >print>(>'LCA(3, 4) = %d'> %> (findLCA(root,>3>,>4>)))> >print>(>'LCA(2, 4) = %d'> %> (findLCA(root,>2>,>4>)))> # This code is contributed by Nikhil Kumar Singh(nickzuck_007)> |
>
>
C#
// C# Program for Lowest Common> // Ancestor in a Binary Tree> // A O(n) solution to find LCA> // of two given values n1 and n2> using> System.Collections;> using> System;> // A Binary Tree node> class> Node {> >public> int> data;> >public> Node left, right;> >public> Node(>int> value)> >{> >data = value;> >left = right =>null>;> >}> }> public> class> BT_NoParentPtr_Solution1 {> >Node root;> >private> ArrayList path1 =>new> ArrayList();> >private> ArrayList path2 =>new> ArrayList();> >// Finds the path from root> >// node to given root of the> >// tree.> >int> findLCA(>int> n1,>int> n2)> >{> >path1.Clear();> >path2.Clear();> >return> findLCAInternal(root, n1, n2);> >}> >private> int> findLCAInternal(Node root,>int> n1,>int> n2)> >{> >if> (!findPath(root, n1, path1)> >|| !findPath(root, n2, path2)) {> >Console.Write((path1.Count>0)> >?>'n1 is present'> >:>'n1 is missing'>);> >Console.Write((path2.Count>0)> >?>'n2 is present'> >:>'n2 is missing'>);> >return> -1;> >}> >int> i;> >for> (i = 0; i i++) { // System.out.println(path1.get(i) // + ' ' + path2.get(i)); if ((int)path1[i] != (int)path2[i]) break; } return (int)path1[i - 1]; } // Finds the path from root node // to given root of the tree, // Stores the path in a vector // path[], returns true if path // exists otherwise false private bool findPath(Node root, int n, ArrayList path) { // base case if (root == null) { return false; } // Store this node . The node // will be removed if not in // path from root to n. path.Add(root.data); if (root.data == n) { return true; } if (root.left != null && findPath(root.left, n, path)) { return true; } if (root.right != null && findPath(root.right, n, path)) { return true; } // If not present in subtree // rooted with root, remove root // from path[] and return false path.RemoveAt(path.Count - 1); return false; } // Driver code public static void Main(String[] args) { BT_NoParentPtr_Solution1 tree = new BT_NoParentPtr_Solution1(); tree.root = new Node(1); tree.root.left = new Node(2); tree.root.right = new Node(3); tree.root.left.left = new Node(4); tree.root.left.right = new Node(5); tree.root.right.left = new Node(6); tree.root.right.right = new Node(7); Console.Write('LCA(4, 5) = ' + tree.findLCA(4, 5)); Console.Write('
LCA(4, 6) = ' + tree.findLCA(4, 6)); Console.Write('
LCA(3, 4) = ' + tree.findLCA(3, 4)); Console.Write('
LCA(2, 4) = ' + tree.findLCA(2, 4)); } } // This code is contributed by Rutvik_56> |
>
>
Javascript
> >// JavaScript Program for Lowest Common> >// Ancestor in a Binary Tree> >// A O(n) solution to find LCA of> >// two given values n1 and n2> > >class Node> >{> >constructor(value) {> >this>.left =>null>;> >this>.right =>null>;> >this>.data = value;> >}> >}> > >let root;> >let path1 = [];> >let path2 = [];> > >// Finds the path from root node to given root of the tree.> >function> findLCA(n1, n2) {> >path1 = [];> >path2 = [];> >return> findLCAInternal(root, n1, n2);> >}> > >function> findLCAInternal(root, n1, n2) {> > >if> (!findPath(root, n1, path1) || !findPath(root, n2, path2))> >{> >document.write((path1.length>0)?> >'n1 is present'> :>'n1 is missing'>);> >document.write((path2.length>0)?> >'n2 is present'> :>'n2 is missing'>);> >return> -1;> >}> > >let i;> >for> (i = 0; i // System.out.println(path1.get(i) + ' ' + path2.get(i)); if (path1[i] != path2[i]) break; } return path1[i-1]; } // Finds the path from root node to // given root of the tree, Stores the // path in a vector path[], returns true // if path exists otherwise false function findPath(root, n, path) { // base case if (root == null) { return false; } // Store this node . The node will be removed if // not in path from root to n. path.push(root.data); if (root.data == n) { return true; } if (root.left != null && findPath(root.left, n, path)) { return true; } if (root.right != null && findPath(root.right, n, path)) { return true; } // If not present in subtree rooted with root, // remove root from // path[] and return false path.pop(); return false; } root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); root.right.left = new Node(6); root.right.right = new Node(7); document.write('LCA(4, 5) = ' + findLCA(4,5) + ''); document.write('LCA(4, 6) = ' + findLCA(4,6) + ''); document.write('LCA(3, 4) = ' + findLCA(3,4) + ''); document.write('LCA(2, 4) = ' + findLCA(2,4));> |
>
>Izhod
LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3, 4) = 1 LCA(2, 4) = 2>
Časovna zapletenost: O(N). Drevo se prečka dvakrat, nato pa se nizi poti primerjajo.
Pomožni prostor: O(N). Dodaten prostor za path1 in path2.
Najnižji skupni prednik v binarnem drevesu z enim prehodom:
Ideja je prečkati drevo, začenši s korenino. Če se kateri koli od danih ključev (n1 in n2) ujema s korenom, potem je koren LCA (ob predpostavki, da sta prisotna oba ključa). Če se koren ne ujema z nobenim od ključev, se ponovimo za levo in desno poddrevo.
- Vozlišče, ki ima en ključ v levem poddrevesu in drugi ključ v desnem poddrevesu, je LCA.
- Če oba ključa ležita v levem poddrevesu, ima tudi levo poddrevo LCA,
- V nasprotnem primeru LCA leži v desnem poddrevesu.
Ilustracija:
Poiščite LCA za 5 in 6
Root kaže na vozlišče z vrednostjo 1, ker se njegova vrednost ne ujema z { 5, 6 }. Ključ iščemo v levem in desnem poddrevesu.
- Levo poddrevo:
- Nov koren = { 2 } ≠ 5 ali 6, zato bomo nadaljevali našo rekurzijo
- New Root = { 4 }, njegovo levo in desno poddrevo je ničelno, za ta klic bomo vrnili NULL
- New Root = { 5 }, vrednost se ujema s 5, tako da bo vrnil vozlišče z vrednostjo 5
- Klic funkcije za root z vrednostjo 2 bo vrnil vrednost 5
- Desno poddrevo:
- Koren = { 3 } ≠ 5 ali 6, zato nadaljujemo našo rekurzijo
- Root = { 6 } = 5 ali 6, bomo vrnili to vozlišče z vrednostjo 6
- Root = { 7 } ≠ 5 ali 6, bomo vrnili NULL
- Torej bo klic funkcije za root z vrednostjo 3 vrnil vozlišče z vrednostjo 6
- Ker levo poddrevo in desno poddrevo vozlišča z vrednostjo 1 nista NULL, je 1 LCA
Za rešitev težave sledite spodnjim korakom:
- Koren posredujemo pomožni funkciji in preverimo, ali se vrednost korena ujema s katerim od n1 in n2.
- Če je odgovor DA, vrnite koren
- else rekurzivni klic na levem in desnem poddrevesu
- V bistvu izvajamo prehod pred naročilom, najprej preverimo, ali se korenska vrednost ujema z n1 ali n2. Nato prečkajte levo in desno poddrevo.
- Če obstaja kateri koli koren, ki vrne eno vrednost NULL in drugo vrednost NON-NULL, bomo za to vozlišče vrnili ustrezno vrednost NON-NULL.
- Vozlišče, ki vrne obe vrednosti NON-NULL za levo in desno poddrevo, je naš najnižji skupni prednik.
Spodaj je implementacija zgornjega pristopa.
C++
/* C++ Program to find LCA of n1 and n2 using one traversal> >* of Binary Tree */> #include> using> namespace> std;> // A Binary Tree Node> struct> Node {> >struct> Node *left, *right;> >int> key;> };> // Utility function to create a new tree Node> Node* newNode(>int> key)> {> >Node* temp =>new> Node;> >temp->ključ = ključ;> >temp->levo = temp->desno = NULL;> >return> temp;> }> // This function returns pointer to LCA of two given values> // n1 and n2. This function assumes that n1 and n2 are> // present in Binary Tree> struct> Node* findLCA(>struct> Node* root,>int> n1,>int> n2)> > >// Base case> >if> (root == NULL)> >return> NULL;> >// If either n1 or n2 matches with root's key, report> >// the presence by returning root (Note that if a key is> >// ancestor of other, then the ancestor key becomes LCA> >if> (root->ključ == n1> // Driver program to test above functions> int> main()> {> >// Let us create binary tree given in the above example> >Node* root = newNode(1);> >root->levo = novoVozlišče(2);> >root->desno = novoVozlišče(3);> >root->levo->levo = novoVozlišče(4);> >root->levo->desno = novoVozlišče(5);> >root->desno->levo = novoVozlišče(6);> >root->desno->desno = novoVozlišče(7);> >cout <<>'LCA(4, 5) = '> cout << '
LCA(4, 6) = ' cout << '
LCA(3, 4) = ' cout << '
LCA(2, 4) = ' return 0; } // This code is contributed by Aditya Kumar (adityakumar129)> |
>
>
C
// C Program to find LCA of n1 and n2 using one traversalof> // Binary Tree> #include> #include> // A Binary Tree Node> typedef> struct> Node {> >struct> Node *left, *right;> >int> key;> } Node;> // Utility function to create a new tree Node> Node* newNode(>int> key)> {> >Node* temp = (Node*)>malloc>(>sizeof>(Node));> >temp->ključ = ključ;> >temp->levo = temp->desno = NULL;> >return> temp;> }> // This function returns pointer to LCA of two given values> // n1 and n2. This function assumes that n1 and n2 are> // present in Binary Tree> Node* findLCA(Node* root,>int> n1,>int> n2)> > >// Base case> >if> (root == NULL)> >return> NULL;> >// If either n1 or n2 matches with root's key, report> >// the presence by returning root (Note that if a key is> >// ancestor of other, then the ancestor key becomes LCA> >if> (root->ključ == n1> // Driver program to test above functions> int> main()> {> >// Let us create binary tree given in the above example> >Node* root = newNode(1);> >root->levo = novoVozlišče(2);> >root->desno = novoVozlišče(3);> >root->levo->levo = novoVozlišče(4);> >root->levo->desno = novoVozlišče(5);> >root->desno->levo = novoVozlišče(6);> >root->desno->desno = novoVozlišče(7);>> >printf>(>'LCA(4, 5) = %d'>, findLCA(root, 4, 5)->ključ);> >printf>(>'
LCA(4, 6) = %d'>, findLCA(root, 4, 6)->ključ);> >printf>(>'
LCA(3, 4) = %d'>, findLCA(root, 3, 4)->ključ);> >printf>(>'
LCA(2, 4) = %d'>, findLCA(root, 2, 4)->ključ);> >return> 0;> }> // This code is contributed by Aditya Kumar (adityakumar129)> |
>
>
Java
// Java implementation to find lowest common ancestor of> // n1 and n2 using one traversal of binary tree> /* Class containing left and right child of current> >node and key value*/> class> Node {> >int> data;> >Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> public> class> BinaryTree {> >// Root of the Binary Tree> >Node root;> >Node findLCA(>int> n1,>int> n2)> >{> >return> findLCA(root, n1, n2);> >}> >// This function returns pointer to LCA of two given> >// values n1 and n2. This function assumes that n1 and> >// n2 are present in Binary Tree> >Node findLCA(Node node,>int> n1,>int> n2)> >> >// Base case> >if> (node ==>null>)> >return> null>;> >// If either n1 or n2 matches with root's key,> >// report the presence by returning root (Note that> >// if a key is ancestor of other, then the ancestor> >// key becomes LCA> >if> (node.data == n1> >/* Driver program to test above functions */> >public> static> void> main(String args[])> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(>1>);> >tree.root.left =>new> Node(>2>);> >tree.root.right =>new> Node(>3>);> >tree.root.left.left =>new> Node(>4>);> >tree.root.left.right =>new> Node(>5>);> >tree.root.right.left =>new> Node(>6>);> >tree.root.right.right =>new> Node(>7>);> >System.out.println(>'LCA(4, 5) = '> >+ tree.findLCA(>4>,>5>).data);> >System.out.println(>'LCA(4, 6) = '> >+ tree.findLCA(>4>,>6>).data);> >System.out.println(>'LCA(3, 4) = '> >+ tree.findLCA(>3>,>4>).data);> >System.out.println(>'LCA(2, 4) = '> >+ tree.findLCA(>2>,>4>).data);> >}> }> |
>
>
Python3
# Python program to find LCA of n1 and n2 using one> # traversal of Binary tree> # A binary tree node> class> Node:> ># Constructor to create a new tree node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # This function returns pointer to LCA of two given> # values n1 and n2> # This function assumes that n1 and n2 are present in> # Binary Tree> def> findLCA(root, n1, n2):> ># Base Case> >if> root>is> None>:> >return> None> ># If either n1 or n2 matches with root's key, report> ># the presence by returning root (Note that if a key is> ># ancestor of other, then the ancestor key becomes LCA> >if> root.key>=>=> n1>or> root.key>=>=> n2:> >return> root> ># Look for keys in left and right subtrees> >left_lca>=> findLCA(root.left, n1, n2)> >right_lca>=> findLCA(root.right, n1, n2)> ># If both of the above calls return Non-NULL, then one key> ># is present in once subtree and other is present in other,> ># So this node is the LCA> >if> left_lca>and> right_lca:> >return> root> ># Otherwise check if left subtree or right subtree is LCA> >return> left_lca>if> left_lca>is> not> None> else> right_lca> # Driver code> if> __name__>=>=> '__main__'>:> > ># Let us create a binary tree given in the above example> >root>=> Node(>1>)> >root.left>=> Node(>2>)> >root.right>=> Node(>3>)> >root.left.left>=> Node(>4>)> >root.left.right>=> Node(>5>)> >root.right.left>=> Node(>6>)> >root.right.right>=> Node(>7>)> >print>(>'LCA(4, 5) = '>, findLCA(root,>4>,>5>).key)> >print>(>'LCA(4, 6) = '>, findLCA(root,>4>,>6>).key)> >print>(>'LCA(3, 4) = '>, findLCA(root,>3>,>4>).key)> >print>(>'LCA(2, 4) = '>, findLCA(root,>2>,>4>).key)> # This code is contributed by Nikhil Kumar Singh(nickzuck_007)> |
>
>
C#
// C# implementation to find lowest common> // ancestor of n1 and n2 using one traversal> // of binary tree> using> System;> // Class containing left and right> // child of current node and key value> public> class> Node {> >public> int> data;> >public> Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> class> BinaryTree {> >// Root of the Binary Tree> >Node root;> >Node findLCA(>int> n1,>int> n2)> >{> >return> findLCA(root, n1, n2);> >}> >// This function returns pointer to LCA> >// of two given values n1 and n2. This> >// function assumes that n1 and n2 are> >// present in Binary Tree> >Node findLCA(Node node,>int> n1,>int> n2)> > node.data == n2)> >return> node;> >// Look for keys in left and right subtrees> >Node left_lca = findLCA(node.left, n1, n2);> >Node right_lca = findLCA(node.right, n1, n2);> >// If both of the above calls return Non-NULL,> >// then one key is present in once subtree> >// and other is present in other, So this> >// node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>)> >return> node;> >// Otherwise check if left subtree or> >// right subtree is LCA> >return> (left_lca !=>null>) ? left_lca : right_lca;> >> >// Driver code> >public> static> void> Main(>string>[] args)> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(1);> >tree.root.left =>new> Node(2);> >tree.root.right =>new> Node(3);> >tree.root.left.left =>new> Node(4);> >tree.root.left.right =>new> Node(5);> >tree.root.right.left =>new> Node(6);> >tree.root.right.right =>new> Node(7);> >Console.WriteLine(>'LCA(4, 5) = '> >+ tree.findLCA(4, 5).data);> >Console.WriteLine(>'LCA(4, 6) = '> >+ tree.findLCA(4, 6).data);> >Console.WriteLine(>'LCA(3, 4) = '> >+ tree.findLCA(3, 4).data);> >Console.WriteLine(>'LCA(2, 4) = '> >+ tree.findLCA(2, 4).data);> >}> }> // This code is contributed by pratham76> |
>
>
Javascript
> >// JavaScript implementation to find> >// lowest common ancestor of> >// n1 and n2 using one traversal of binary tree> > >class Node> >{> >constructor(item) {> >this>.left =>null>;> >this>.right =>null>;> >this>.data = item;> >}> >}> > >//Root of the Binary Tree> >let root;> > >function> findlCA(n1, n2)> >{> >return> findLCA(root, n1, n2);> >}> > >// This function returns pointer to LCA of two given> >// values n1 and n2. This function assumes that n1 and> >// n2 are present in Binary Tree> >function> findLCA(node, n1, n2)> >> > >root =>new> Node(1);> >root.left =>new> Node(2);> >root.right =>new> Node(3);> >root.left.left =>new> Node(4);> >root.left.right =>new> Node(5);> >root.right.left =>new> Node(6);> >root.right.right =>new> Node(7);> >document.write(>'LCA(4, 5) = '> +> >findlCA(4, 5).data +>''>);> >document.write(>'LCA(4, 6) = '> +> >findlCA(4, 6).data +>''>);> >document.write(>'LCA(3, 4) = '> +> >findlCA(3, 4).data +>''>);> >document.write(>'LCA(2, 4) = '> +> >findlCA(2, 4).data +>''>);> > > |
>
>Izhod
LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3, 4) = 1 LCA(2, 4) = 2>
Časovna zapletenost : O(N) kot metoda izvaja preprosto prečkanje drevesa na način od spodaj navzgor.
Pomožni prostor: O(H), kjer je H višina drevesa.
Opomba: Zgornja metoda predvideva, da ključi so prisotni v binarnem drevesu . Če je en ključ prisoten, drugega pa ni, vrne trenutni ključ kot LCA (v idealnem primeru bi moral vrniti NULL). To metodo lahko razširimo za obravnavo vseh primerov tako, da najprej preverimo, ali sta n1 in n2 prisotna v drevesu, nato pa poiščemo LCA za n1 in n2. Če želite preveriti, ali je vozlišče prisotno v binarnem drevesu ali ne, nato prečkajte drevo za vozlišča n1 in n2 ločeno.
C++
/* C++ program to find LCA of n1 and n2 using one traversal> >of Binary Tree. It handles all cases even when n1 or n2> >is not there in Binary Tree */> #include> using> namespace> std;> // A Binary Tree Node> struct> Node {> >struct> Node *left, *right;> >int> key;> };> // Utility function to create a new tree Node> Node* newNode(>int> key)> {> >Node* temp =>new> Node;> >temp->ključ = ključ;> >temp->levo = temp->desno = NULL;> >return> temp;> }> // This function returns pointer to LCA of two given> // valuesn1 and n2.> struct> Node* findLCAUtil(>struct> Node* root,>int> n1,>int> n2)> > // Returns true if key k is present in tree rooted with root> bool> find(Node* root,>int> k)> find(root->desno, k))> >return> true>;> >// Else return false> >return> false>;> > // This function returns LCA of n1 and n2 only if both n1> // and n2 are present in tree, otherwise returns NULL;> Node* findLCA(Node* root,>int> n1,>int> n2)> {> >// Return LCA only if both n1 and n2 are present in tree> >if> (find(root, n1) and find(root, n2))> >return> findLCAUtil(root, n1, n2);> >// Else return NULL> >return> NULL;> }> // Driver program to test above functions> int> main()> {> >// Let us create a binary tree given in the above> >// example> >Node* root = newNode(1);> >root->levo = novoVozlišče(2);> >root->desno = novoVozlišče(3);> >root->levo->levo = novoVozlišče(4);> >root->levo->desno = novoVozlišče(5);> >root->desno->levo = novoVozlišče(6);>> >root->desno->desno = novoVozlišče(7);> >Node* lca = findLCA(root, 4, 5);> >if> (lca != NULL)> >cout <<>'LCA(4, 5) = '> else cout << 'Keys are not present '; lca = findLCA(root, 4, 10); if (lca != NULL) cout << '
LCA(4, 10) = ' else cout << '
Keys are not present '; return 0; } // This code is contributed by Kshitij Dwivedi // (kshitijdwivedi28)> |
>
>
Java
// Java implementation to find lowest common ancestor of> // n1 and n2 using one traversal of binary tree> // It also handles cases even when n1 and n2 are not there> // in Tree> /* Class containing left and right child of current node and> >* key */> class> Node {> >int> data;> >Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> public> class> BinaryTree {> >// Root of the Binary Tree> >Node root;> >static> boolean> v1 =>false>, v2 =>false>;> >// This function returns pointer to LCA of two given> >// values n1 and n2.> >// v1 is set as true by this function if n1 is found> >// v2 is set as true by this function if n2 is found> >Node findLCAUtil(Node node,>int> n1,>int> n2)> >{> >// Base case> >if> (node ==>null>)> >return> null>;> >// Store result in temp, in case of key match so> >// that we can search for other key also.> >Node temp =>null>;> >// If either n1 or n2 matches with root's key,> >// report the presence by setting v1 or v2 as true> >// and return root (Note that if a key is ancestor> >// of other, then the ancestor key becomes LCA)> >if> (node.data == n1) {> >v1 =>true>;> >temp = node;> >}> >if> (node.data == n2) {> >v2 =>true>;> >temp = node;> >}> >// Look for keys in left and right subtrees> >Node left_lca = findLCAUtil(node.left, n1, n2);> >Node right_lca = findLCAUtil(node.right, n1, n2);> >if> (temp !=>null>)> >return> temp;> >// If both of the above calls return Non-NULL, then> >// one key is present in once subtree and other is> >// present in other, So this node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>)> >return> node;> >// Otherwise check if left subtree or right subtree> >// is LCA> >return> (left_lca !=>null>) ? left_lca : right_lca;> >}> >// Finds lca of n1 and n2 under the subtree rooted with> >// 'node'> >Node findLCA(>int> n1,>int> n2)> >{> >// Initialize n1 and n2 as not visited> >v1 =>false>;> >v2 =>false>;> >// Find lca of n1 and n2 using the technique> >// discussed above> >Node lca = findLCAUtil(root, n1, n2);> >// Return LCA only if both n1 and n2 are present in> >// tree> >if> (v1 && v2)> >return> lca;> >// Else return NULL> >return> null>;> >}> >/* Driver program to test above functions */> >public> static> void> main(String args[])> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(>1>);> >tree.root.left =>new> Node(>2>);> >tree.root.right =>new> Node(>3>);> >tree.root.left.left =>new> Node(>4>);> >tree.root.left.right =>new> Node(>5>);> >tree.root.right.left =>new> Node(>6>);> >tree.root.right.right =>new> Node(>7>);> >Node lca = tree.findLCA(>4>,>5>);> >if> (lca !=>null>)> >System.out.println(>'LCA(4, 5) = '> + lca.data);> >else> >System.out.println(>'Keys are not present'>);> >lca = tree.findLCA(>4>,>10>);> >if> (lca !=>null>)> >System.out.println(>'LCA(4, 10) = '> + lca.data);> >else> >System.out.println(>'Keys are not present'>);> >}> }> |
>
>
Python3
''' Program to find LCA of n1 and n2 using one traversal of> >Binary tree> It handles all cases even when n1 or n2 is not there in tree> '''> # A binary tree node> class> Node:> ># Constructor to create a new node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # This function return pointer to LCA of two given values> # n1 and n2> # v1 is set as true by this function if n1 is found> # v2 is set as true by this function if n2 is found> def> findLCAUtil(root, n1, n2, v):> ># Base Case> >if> root>is> None>:> >return> None> ># IF either n1 or n2 matches ith root's key, report> ># the presence by setting v1 or v2 as true and return> ># root (Note that if a key is ancestor of other, then> ># the ancestor key becomes LCA)> >if> root.key>=>=> n1:> >v[>0>]>=> True> >return> root> >if> root.key>=>=> n2:> >v[>1>]>=> True> >return> root> ># Look for keys in left and right subtree> >left_lca>=> findLCAUtil(root.left, n1, n2, v)> >right_lca>=> findLCAUtil(root.right, n1, n2, v)> ># If both of the above calls return Non-NULL, then one key> ># is present in once subtree and other is present in other,> ># So this node is the LCA> >if> left_lca>and> right_lca:> >return> root> ># Otherwise check if left subtree or right subtree is LCA> >return> left_lca>if> left_lca>is> not> None> else> right_lca> def> find(root, k):> ># Base Case> >if> root>is> None>:> >return> False> ># If key is present at root, or if left subtree or right> ># subtree , return true> >if> (root.key>=>=> k>or> find(root.left, k)>or> >find(root.right, k)):> >return> True> ># Else return false> >return> False> # This function returns LCA of n1 and n2 on value if both> # n1 and n2 are present in tree, otherwise returns None> def> findLCA(root, n1, n2):> ># Initialize n1 and n2 as not visited> >v>=> [>False>,>False>]> ># Find lca of n1 and n2 using the technique discussed above> >lca>=> findLCAUtil(root, n1, n2, v)> ># Returns LCA only if both n1 and n2 are present in tree> >if> (v[>0>]>and> v[>1>]>or> v[>0>]>and> find(lca, n2)>or> v[>1>]>and> >find(lca, n1)):> >return> lca> ># Else return None> >return> None> # Driver program to test above function> root>=> Node(>1>)> root.left>=> Node(>2>)> root.right>=> Node(>3>)> root.left.left>=> Node(>4>)> root.left.right>=> Node(>5>)> root.right.left>=> Node(>6>)> root.right.right>=> Node(>7>)> lca>=> findLCA(root,>4>,>5>)> if> lca>is> not> None>:> >print>(>'LCA(4, 5) = '>, lca.key)> else>:> >print>(>'Keys are not present'>)> lca>=> findLCA(root,>4>,>10>)> if> lca>is> not> None>:> >print>(>'LCA(4,10) = '>, lca.key)> else>:> >print>(>'Keys are not present'>)> # This code is contributed by Nikhil Kumar Singh(nickzuck_007)> |
>
>
C#
using> System;> // c# implementation to find lowest common ancestor of> // n1 and n2 using one traversal of binary tree> // It also handles cases even when n1 and n2 are not there> // in Tree> /* Class containing left and right child of current node and> >* key */> public> class> Node {> >public> int> data;> >public> Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> public> class> BinaryTree {> >// Root of the Binary Tree> >public> Node root;> >public> static> bool> v1 =>false>, v2 =>false>;> >// This function returns pointer to LCA of two given> >// values n1 and n2.> >// v1 is set as true by this function if n1 is found> >// v2 is set as true by this function if n2 is found> >public> virtual> Node findLCAUtil(Node node,>int> n1,> >int> n2)> >{> >// Base case> >if> (node ==>null>) {> >return> null>;> >}> >// Store result in temp, in case of key match so> >// that we can search for other key also.> >Node temp =>null>;> >// If either n1 or n2 matches with root's key,> >// report the presence by setting v1 or v2 as true> >// and return root (Note that if a key is ancestor> >// of other, then the ancestor key becomes LCA)> >if> (node.data == n1) {> >v1 =>true>;> >temp = node;> >}> >if> (node.data == n2) {> >v2 =>true>;> >temp = node;> >}> >// Look for keys in left and right subtrees> >Node left_lca = findLCAUtil(node.left, n1, n2);> >Node right_lca = findLCAUtil(node.right, n1, n2);> >if> (temp !=>null>) {> >return> temp;> >}> >// If both of the above calls return Non-NULL, then> >// one key is present in once subtree and other is> >// present in other, So this node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>) {> >return> node;> >}> >// Otherwise check if left subtree or right subtree> >// is LCA> >return> (left_lca !=>null>) ? left_lca : right_lca;> >}> >// Finds lca of n1 and n2 under the subtree rooted with> >// 'node'> >public> virtual> Node findLCA(>int> n1,>int> n2)> >{> >// Initialize n1 and n2 as not visited> >v1 =>false>;> >v2 =>false>;> >// Find lca of n1 and n2 using the technique> >// discussed above> >Node lca = findLCAUtil(root, n1, n2);> >// Return LCA only if both n1 and n2 are present in> >// tree> >if> (v1 && v2) {> >return> lca;> >}> >// Else return NULL> >return> null>;> >}> >/* Driver program to test above functions */> >public> static> void> Main(>string>[] args)> >{> >BinaryTree tree =>new> BinaryTree();> >tree.root =>new> Node(1);> >tree.root.left =>new> Node(2);> >tree.root.right =>new> Node(3);> >tree.root.left.left =>new> Node(4);> >tree.root.left.right =>new> Node(5);> >tree.root.right.left =>new> Node(6);> >tree.root.right.right =>new> Node(7);> >Node lca = tree.findLCA(4, 5);> >if> (lca !=>null>) {> >Console.WriteLine(>'LCA(4, 5) = '> + lca.data);> >}> >else> {> >Console.WriteLine(>'Keys are not present'>);> >}> >lca = tree.findLCA(4, 10);> >if> (lca !=>null>) {> >Console.WriteLine(>'LCA(4, 10) = '> + lca.data);> >}> >else> {> >Console.WriteLine(>'Keys are not present'>);> >}> >}> }> // This code is contributed by Shrikant13> |
>
>
Javascript
> // JavaScript implementation to find lowest> // common ancestor of n1 and n2 using one> // traversal of binary tree. It also handles> // cases even when n1 and n2 are not there in Tree> // Class containing left and right child> // of current node and key> class Node> {> >constructor(item)> >{> >this>.data = item;> >this>.left =>null>;> >this>.right =>null>;> >}> }> class BinaryTree{> > // Root of the Binary Tree> constructor()> {> >this>.root =>null>;> >this>.v1 =>false>;> >this>.v2 =>false>;> }> // This function returns pointer to LCA> // of two given values n1 and n2.> // v1 is set as true by this function> // if n1 is found> // v2 is set as true by this function> // if n2 is found> findLCAUtil(node, n1, n2)> {> > >// Base case> >if> (node ==>null>)> >{> >return> null>;> >}> > >// Store result in temp, in case of> >// key match so that we can search> >// for other key also.> >var> temp =>null>;> > >// If either n1 or n2 matches with root's key,> >// report the presence by setting v1 or v2 as> >// true and return root (Note that if a key> >// is ancestor of other, then the ancestor> >// key becomes LCA)> >if> (node.data == n1)> >{> >this>.v1 =>true>;> >temp = node;> >}> >if> (node.data == n2)> >{> >this>.v2 =>true>;> >temp = node;> >}> > >// Look for keys in left and right subtrees> >var> left_lca =>this>.findLCAUtil(node.left, n1, n2);> >var> right_lca =>this>.findLCAUtil(node.right, n1, n2);> > >if> (temp !=>null>)> >{> >return> temp;> >}> > >// If both of the above calls return Non-NULL,> >// then one key is present in once subtree and> >// other is present in other, So this node is the LCA> >if> (left_lca !=>null> && right_lca !=>null>)> >{> >return> node;> >}> > >// Otherwise check if left subtree or> >// right subtree is LCA> >return> left_lca !=>null> ? left_lca : right_lca;> }> // Finds lca of n1 and n2 under the> // subtree rooted with 'node'> findLCA(n1, n2)> {> > >// Initialize n1 and n2 as not visited> >this>.v1 =>false>;> >this>.v2 =>false>;> > >// Find lca of n1 and n2 using the> >// technique discussed above> >var> lca =>this>.findLCAUtil(>this>.root, n1, n2);> > >// Return LCA only if both n1 and n2> >// are present in tree> >if> (>this>.v1 &&>this>.v2)> >{> >return> lca;> >}> > >// Else return NULL> >return> null>;> }> }> // Driver code> var> tree =>new> BinaryTree();> tree.root =>new> Node(1);> tree.root.left =>new> Node(2);> tree.root.right =>new> Node(3);> tree.root.left.left =>new> Node(4);> tree.root.left.right =>new> Node(5);> tree.root.right.left =>new> Node(6);> tree.root.right.right =>new> Node(7);> var> lca = tree.findLCA(4, 5);> if> (lca !=>null>)> {> >document.write(>'LCA(4, 5) = '> +> >lca.data +>' '>);> }>else> {> >document.write(>'Keys are not present'> +>' '>);> }> lca = tree.findLCA(4, 10);> if> (lca !=>null>)> {> >document.write(>'LCA(4, 10) = '> +> >lca.data +>' '>);> }> else> {> >document.write(>'Keys are not present'> +>' '>);> }> // This code is contributed by rdtank> > |
>
>Izhod
LCA(4, 5) = 2 Keys are not present>
Časovna zapletenost : O(N) kot metoda izvaja preprosto prečkanje drevesa na način od spodaj navzgor.
Pomožni prostor: O(H), kjer je h višina drevesa.
Uporaba pomožne podatkovne strukture (zgoščena tabela):
The basic idea behind the 'Using an auxiliary data structure' approach for finding the lowest common ancestor of two nodes in a binary tree is to use a hash table or a map to store the parent pointers of each node. Once we have the parent pointers, we can traverse up from the first node and add all its ancestors to a set or a list. Then we can traverse up from the second node and check if each ancestor is already in the set or the list. The first ancestor that is already in the set or the list is the lowest common ancestor.>
Sledite korakom za izvedbo zgornjega pristopa:
- Ustvarite zgoščeno tabelo ali zemljevid za shranjevanje nadrejenih kazalcev vsakega vozlišča v binarnem drevesu.
- Prečkajte binarno drevo in napolnite zgoščeno tabelo ali zemljevid z nadrejenimi kazalci za vsako vozlišče.
- Začenši s prvim vozliščem, pojdite po drevesu navzgor in dodajte vsakega prednika v niz ali seznam.
- Začenši od drugega vozlišča, se pomaknite po drevesu navzgor in preverite, ali je vsak prednik že v nizu ali na seznamu. Prvi prednik, ki je že v nizu ali na seznamu, je najnižji skupni prednik.
- Če ni najden skupni prednik, vrnite vrednost null ali katero koli drugo vrednost, ki kaže na odsotnost skupnega prednika.
Spodaj je izvedba za zgornji pristop:
C++
// C++ code to implement above approach> #include> #include> #include> #include> using> namespace> std;> // Definition of a binary tree node> struct> Node {> >int> data;> >Node* left;> >Node* right;> };> // Function to create a new binary tree node> Node* newNode(>int> data)> {> >Node* node =>new> Node;> >node->podatki = podatki;> >node->levo = NULL;> >node->desno = NULL;> >return> (node);> }> // Function to build a hash table or a map of parent> // pointers for each node in the tree> unordered_map buildParentMap(Node* root)> {> >unordered_map parentMap;> >parentMap[root] = NULL;> >vector queue = { root };> >while> (!queue.empty()) {> >Node* node = queue.front();> >queue.erase(queue.begin());> >if> (node->levo) {> >parentMap[node->levo] = vozlišče;> >queue.push_back(node->levo);> >}> >if> (node->desno) {> >parentMap[node->desno] = vozlišče;> >queue.push_back(node->desno);> >}> >}> >return> parentMap;> }> // Function to find the lowest common ancestor of two nodes> // using an auxiliary data structure> int> findLCA(Node* root,>int> n1,>int> n2)> {> >// Build a hash table or a map of parent pointers for> >// each node in the tree> >unordered_map parentMap> >= buildParentMap(root);> >// Find the nodes with values n1 and n2> >Node* p = NULL;> >Node* q = NULL;> >vector queue = { root };> >while> (!queue.empty()) {> >Node* node = queue.front();> >queue.erase(queue.begin());> >if> (node->podatki == n1) {> >p = node;> >}> >if> (node->podatki == n2) {> >q = node;> >}> >if> (node->levo) {> >queue.push_back(node->levo);> >}> >if> (node->desno) {> >queue.push_back(node->desno);> >}> >}> >// Add all the ancestors of the first node to a set or a> >// list> >set ancestors;> >while> (p) {> >ancestors.insert(p);> >p = parentMap[p];> >}> >// Traverse up from the second node and check if each> >// ancestor is already in the set or the list> >while> (q) {> >if> (ancestors.find(q) != ancestors.end()) {> >return> q> >->podatki;>// The first ancestor that is> >// already in the set or the list is> >// the lowest common ancestor> >}> >q = parentMap[q];> >}> >return> -1;>// No common ancestor found> }> // Driver code> int> main()> {> >Node* root = newNode(1);> >root->levo = novoVozlišče(2);> >root->desno = novoVozlišče(3);> >root->levo->levo = novoVozlišče(4);> >root->levo->desno = novoVozlišče(5);> >root->desno->levo = novoVozlišče(6);> >root->desno->desno = novoVozlišče(7);> >cout <<>'LCA(4, 5) = '> << findLCA(root, 4, 5) << endl;> >cout <<>'LCA(4, 6) = '> << findLCA(root, 4, 6) << endl;> >cout <<>'LCA(3,4) = '> << findLCA(root, 3, 4) << endl;> >cout <<>'LCA(2, 4) = '> << findLCA(root, 2, 4) << endl;> >return> 0;> }> // This code is contributed by Veerendra_Singh_Rajpoot> |
>
>
Java
import> java.util.*;> // Definition of a binary tree node> class> Node {> >int> data;> >Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> class> Main {> >// Function to build a hash table or a map of parent> >// pointers for each node in the tree> >static> Map buildParentMap(Node root)> >{> >Map parentMap =>new> HashMap();> >parentMap.put(root,>null>);> >Queue queue =>new> LinkedList();> >queue.add(root);> >while> (!queue.isEmpty()) {> >Node node = queue.poll();> >if> (node.left !=>null>) {> >parentMap.put(node.left, node);> >queue.add(node.left);> >}> >if> (node.right !=>null>) {> >parentMap.put(node.right, node);> >queue.add(node.right);> >}> >}> >return> parentMap;> >}> >// Function to find the lowest common ancestor of two> >// nodes using an auxiliary data structure> >static> int> findLCA(Node root,>int> n1,>int> n2)> >{> >// Build a hash table or a map of parent pointers> >// for each node in the tree> >Map parentMap = buildParentMap(root);> >// Find the nodes with values n1 and n2> >Node p =>null>, q =>null>;> >Queue queue =>new> LinkedList();> >queue.add(root);> >while> (!queue.isEmpty()) {> >Node node = queue.poll();> >if> (node.data == n1) {> >p = node;> >}> >if> (node.data == n2) {> >q = node;> >}> >if> (node.left !=>null>) {> >queue.add(node.left);> >}> >if> (node.right !=>null>) {> >queue.add(node.right);> >}> >}> >// Add all the ancestors of the first node to a set> >// or a list> >Set ancestors =>new> HashSet();> >while> (p !=>null>) {> >ancestors.add(p);> >p = parentMap.get(p);> >}> >// Traverse up from the second node and check if> >// each ancestor is already in the set or the list> >while> (q !=>null>) {> >if> (ancestors.contains(q)) {> >return> q.data;> >}> >q = parentMap.get(q);> >}> >return> ->1>;>// No common ancestor found> >}> >public> static> void> main(String[] args)> >{> >Node root =>new> Node(>1>);> >root.left =>new> Node(>2>);> >root.right =>new> Node(>3>);> >root.left.left =>new> Node(>4>);> >root.left.right =>new> Node(>5>);> >root.right.left =>new> Node(>6>);> >root.right.right =>new> Node(>7>);> >System.out.println(>'LCA(4, 5) = '> >+ findLCA(root,>4>,>5>));> >System.out.println(>'LCA(4, 6) = '> >+ findLCA(root,>4>,>6>));> >System.out.println(>'LCA(3, 4) = '> >+ findLCA(root,>3>,>4>));> >System.out.println(>'LCA(3, 4) = '> >+ findLCA(root,>2>,>4>));> >}> }> |
>
>
Python3
from> collections>import> deque> # Definition of a binary tree node> class> Node:> >def> __init__(>self>, data):> >self>.data>=> data> >self>.left>=> None> >self>.right>=> None> # Function to build a hash table or a map of parent> # pointers for each node in the tree> def> buildParentMap(root):> >parentMap>=> {}> >parentMap[root]>=> None> >queue>=> deque([root])> >while> queue:> >node>=> queue.popleft()> >if> node.left:> >parentMap[node.left]>=> node> >queue.append(node.left)> >if> node.right:> >parentMap[node.right]>=> node> >queue.append(node.right)> >return> parentMap> # Function to find the lowest common ancestor of two nodes> # using an auxiliary data structure> def> findLCA(root, n1, n2):> ># Build a hash table or a map of parent pointers for> ># each node in the tree> >parentMap>=> buildParentMap(root)> ># Find the nodes with values n1 and n2> >p, q>=> None>,>None> >queue>=> deque([root])> >while> queue:> >node>=> queue.popleft()> >if> node.data>=>=> n1:> >p>=> node> >if> node.data>=>=> n2:> >q>=> node> >if> node.left:> >queue.append(node.left)> >if> node.right:> >queue.append(node.right)> ># Add all the ancestors of the first node to a set or a> ># list> >ancestors>=> set>()> >while> p:> >ancestors.add(p)> >p>=> parentMap[p]> ># Traverse up from the second node and check if each> ># ancestor is already in the set or the list> >while> q:> >if> q>in> ancestors:> >return> q.data> >q>=> parentMap[q]> >return> ->1> # No common ancestor found> # Driver code> if> __name__>=>=> '__main__'>:> >root>=> Node(>1>)> >root.left>=> Node(>2>)> >root.right>=> Node(>3>)> >root.left.left>=> Node(>4>)> >root.left.right>=> Node(>5>)> >root.right.left>=> Node(>6>)> >root.right.right>=> Node(>7>)> >print>(>'LCA(4, 5) = '>, findLCA(root,>4>,>5>))> >print>(>'LCA(4, 6) = '>, findLCA(root,>4>,>6>))> >print>(>'LCA(3, 4) = '>, findLCA(root,>3>,>4>))> >print>(>'LCA(2, 4) = '>, findLCA(root,>2>,>4>))> |
>
>
C#
using> System;> using> System.Collections.Generic;> // Definition of a binary tree node> class> Node> {> >public> int> data;> >public> Node left, right;> >public> Node(>int> item)> >{> >data = item;> >left = right =>null>;> >}> }> class> MainClass> {> >// Function to build a hash table or a map of parent> >// pointers for each node in the tree> >static> Dictionary BuildParentMap(Node root)> >{> >Dictionary parentMap =>new> Dictionary();> >parentMap.Add(root,>null>);> >Queue queue =>new> Queue();> >queue.Enqueue(root);> >while> (queue.Count != 0)> >{> >Node node = queue.Dequeue();> >if> (node.left !=>null>)> >{> >parentMap.Add(node.left, node);> >queue.Enqueue(node.left);> >}> >if> (node.right !=>null>)> >{> >parentMap.Add(node.right, node);> >queue.Enqueue(node.right);> >}> >}> >return> parentMap;> >}> >// Function to find the lowest common ancestor of two> >// nodes using an auxiliary data structure> >static> int> FindLCA(Node root,>int> n1,>int> n2)> >{> >// Build a hash table or a map of parent pointers> >// for each node in the tree> >Dictionary parentMap = BuildParentMap(root);> >// Find the nodes with values n1 and n2> >Node p =>null>, q =>null>;> >Queue queue =>new> Queue();> >queue.Enqueue(root);> >while> (queue.Count != 0)> >{> >Node node = queue.Dequeue();> >if> (node.data == n1)> >{> >p = node;> >}> >if> (node.data == n2)> >{> >q = node;> >}> >if> (node.left !=>null>)> >{> >queue.Enqueue(node.left);> >}> >if> (node.right !=>null>)> >{> >queue.Enqueue(node.right);> >}> >}> >// Add all the ancestors of the first node to a set> >// or a list> >HashSet ancestors =>new> HashSet();> >while> (p !=>null>)> >{> >ancestors.Add(p);> >p = parentMap[p];> >}> >// Traverse up from the second node and check if> >// each ancestor is already in the set or the list> >while> (q !=>null>)> >{> >if> (ancestors.Contains(q))> >{> >return> q.data;> >}> >q = parentMap[q];> >}> >return> -1;>// No common ancestor found> >}> >public> static> void> Main()> >{> >Node root =>new> Node(1);> >root.left =>new> Node(2);> >root.right =>new> Node(3);> >root.left.left =>new> Node(4);> >root.left.right =>new> Node(5);> >root.right.left =>new> Node(6);> >root.right.right =>new> Node(7);> >Console.WriteLine(>'LCA(4, 5) = '> + FindLCA(root, 4, 5));> >Console.WriteLine(>'LCA(4, 6) = '> + FindLCA(root, 4, 6));> >Console.WriteLine(>'LCA(3, 4) = '> + FindLCA(root, 3, 4));> >Console.WriteLine(>'LCA(2, 4) = '> + FindLCA(root, 2, 4));> >}> }> // This code is contributed by akashish__> |
>
>
Javascript
// javascript code addition> // Definition of a binary tree node> class Node {> >constructor(item) {> >this>.data = item;> >this>.left =>null>;> >this>.right =>null>;> >}> }> // Function to build a hash table or a map of parent> // pointers for each node in the tree> function> buildParentMap(root) {> >const parentMap =>new> Map();> >parentMap.set(root,>null>);> >const queue = [];> >queue.push(root);> >while> (queue.length>0) {> >const node = queue.shift();> >if> (node.left !=>null>) {> >parentMap.set(node.left, node);> >queue.push(node.left);> >}> >if> (node.right !=>null>) {> >parentMap.set(node.right, node);> >queue.push(node.right);> >}> >}> >return> parentMap;> }> // Function to find the lowest common ancestor of two> // nodes using an auxiliary data structure> function> findLCA(root, n1, n2) {> >// Build a hash table or a map of parent pointers> >// for each node in the tree> >const parentMap = buildParentMap(root);> >// Find the nodes with values n1 and n2> >let p =>null>, q =>null>;> >const queue = [];> >queue.push(root);> >while> (queue.length>0) {> >const node = queue.shift();> >if> (node.data === n1) {> >p = node;> >}> >if> (node.data === n2) {> >q = node;> >}> >if> (node.left !=>null>) {> >queue.push(node.left);> >}> >if> (node.right !=>null>) {> >queue.push(node.right);> >}> >}> >// Add all the ancestors of the first node to a set> >// or a list> >const ancestors =>new> Set();> >while> (p !=>null>) {> >ancestors.add(p);> >p = parentMap.get(p);> >}> >// Traverse up from the second node and check if> >// each ancestor is already in the set or the list> >while> (q !=>null>) {> >if> (ancestors.has(q)) {> >return> q.data;> >}> >q = parentMap.get(q);> >}> >return> -1;>// No common ancestor found> }> // Test the function> const root =>new> Node(1);> root.left =>new> Node(2);> root.right =>new> Node(3);> root.left.left =>new> Node(4);> root.left.right =>new> Node(5);> root.right.left =>new> Node(6);> root.right.right =>new> Node(7);> console.log(>'LCA(4, 5) = '> + findLCA(root, 4, 5));> console.log(>'LCA(4, 6) = '> + findLCA(root, 4, 6));> console.log(>'LCA(3, 4) = '> + findLCA(root, 3, 4));> console.log(>'LCA(2, 4) = '> + findLCA(root, 2, 4));> // The code is contributed by Nidhi goel.> |
>
>Izhod
LCA(4, 5) = 2 LCA(4, 6) = 1 LCA(3,4) = 1 LCA(2, 4) = 2>
Časovna zahtevnost: O(n),
.naslednja java
Časovna kompleksnost podane kode je O(n), kjer je n število vozlišč v binarnem drevesu.
Izdelava nadrejenega zemljevida za vsako vozlišče v drevesu zahteva enkratni obisk vsakega vozlišča, kar traja O(n) časa. Iskanje vozlišč z vrednostma n1 in n2 zahteva obisk vsakega vozlišča enkrat, kar prav tako traja O(n) časa. Prehod od drugega vozlišča navzgor in preverjanje, ali je vsak prednik že v nizu ali na seznamu, traja O(h) časa, kjer je h višina binarnega drevesa.
V najslabšem primeru je višina binarnega drevesa O(n), če je binarno drevo poševno. Zato je skupna časovna kompleksnost dane kode O(n) + O(n) + O(n) = O(n).
Kompleksnost prostora: O(n),
Prostorska kompleksnost podane kode je v najslabšem primeru O(n). To je zato, ker je velikost nadrejenega zemljevida, zgrajenega za vsako vozlišče v drevesu, O(n). Poleg tega lahko nabor prednikov v najslabšem primeru vsebuje tudi vsa vozlišča v binarnem drevesu, kar prav tako zavzame O(n) prostora. Končno čakalna vrsta, ki se uporablja za prečkanje binarnega drevesa, zavzame O(n) prostora. Zato je skupna kompleksnost prostora dane kode O(n) + O(n) + O(n) = O(n).
Razpravljali smo o učinkoviti rešitvi za iskanje LCA v binarnem iskalnem drevesu. V binarnem iskalnem drevesu lahko z uporabo lastnosti BST najdemo LCA v času O(h), kjer je h višina drevesa. Takšna izvedba v binarnem drevesu ni mogoča, saj vozlišča ključev binarnega drevesa ne sledijo nobenemu vrstnemu redu.
Morda si boste želeli ogledati tudi spodnje članke:
LCA z uporabo nadrejenega kazalca
Najnižji skupni prednik v binarnem iskalnem drevesu.
Poiščite LCA v binarnem drevesu z uporabo RMQ
