Logistična regresija v programiranju R je klasifikacijski algoritem, ki se uporablja za iskanje verjetnosti uspeha in neuspeha dogodka. Logistična regresija se uporablja, kadar je odvisna spremenljivka binarne narave (0/1, True/False, Da/Ne). Funkcija logit se uporablja kot povezovalna funkcija v binomski porazdelitvi.
Verjetnost binarne spremenljivke izida je mogoče predvideti s tehniko statističnega modeliranja, znano kot logistična regresija. Široko se uporablja v številnih panogah, vključno s trženjem, financami, družboslovjem in medicinskimi raziskavami.
Logistična funkcija, običajno imenovana sigmoidna funkcija, je osnovna ideja, ki podpira logistično regresijo. Ta sigmoidna funkcija se uporablja v logistični regresiji za opis korelacije med napovedovalnimi spremenljivkami in verjetnostjo binarnega izida.

Logistična regresija v programiranju R
nedeterministični končni avtomati
Logistična regresija je znana tudi kot Binomska logistična regresija . Temelji na sigmoidni funkciji, kjer je izhod verjetnost, vhod pa je lahko od -neskončno do +neskončno.
Teorija
Logistična regresija je znana tudi kot generalizirani linearni model. Ker se uporablja kot klasifikacijska tehnika za napovedovanje kvalitativnega odziva, se vrednost y giblje od 0 do 1 in jo je mogoče predstaviti z naslednjo enačbo:

Logistična regresija v programiranju R
str je verjetnost značilnosti zanimanja. Razmerje obetov je opredeljeno kot verjetnost uspeha v primerjavi z verjetnostjo neuspeha. Je ključna predstavitev koeficientov logistične regresije in ima lahko vrednosti med 0 in neskončnostjo. Razmerje obetov 1 je takrat, ko je verjetnost uspeha enaka verjetnosti neuspeha. Razmerje obetov 2 je takrat, ko je verjetnost uspeha dvakrat večja od verjetnosti neuspeha. Razmerje obetov 0,5 je, ko je verjetnost neuspeha dvakrat večja od verjetnosti uspeha.
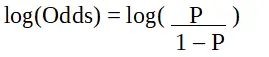
Logistična regresija v programiranju R
Ker delamo z binomsko porazdelitvijo (odvisna spremenljivka), moramo izbrati povezovalno funkcijo, ki je najbolj primerna za to porazdelitev.
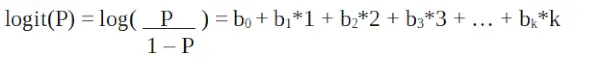
Logistična regresija v programiranju R
Je funkcija logit . V zgornji enačbi je oklepaj izbran tako, da poveča verjetnost opazovanja vzorčnih vrednosti, namesto da zmanjša vsoto kvadratov napak (kot običajna regresija). Logit je znan tudi kot dnevnik kvot. Funkcija logit mora biti linearno povezana z neodvisnimi spremenljivkami. To je iz enačbe A, kjer je leva stran linearna kombinacija x. To je podobno predpostavki OLS, da je y linearno povezan z x. Spremenljivke b0, b1, b2 … itd niso znane in jih je treba oceniti na podlagi razpoložljivih podatkov o usposabljanju. V logističnem regresijskem modelu množenje b1 z eno enoto spremeni logit za b0. Spremembe P zaradi spremembe ene enote bodo odvisne od pomnožene vrednosti. Če je b1 pozitiven, se bo P povečal, če pa je b1 negativen, se bo P zmanjšal.
Nabor podatkov
mtcars (motor trend car road test) obsega porabo goriva, zmogljivost in 10 vidikov avtomobilske zasnove za 32 avtomobilov. Prihaja z vnaprej nameščenim dplyr paket v R.
R
# Installing the package> install.packages>(>'dplyr'>)> # Loading package> library>(dplyr)> # Summary of dataset in package> summary>(mtcars)> |
>
>
Izvajanje logistične regresije na naboru podatkov
Logistična regresija je implementirana v R z uporabo glm() z usposabljanjem modela z uporabo funkcij ali spremenljivk v naboru podatkov.
R
izberite kot
# Installing the package> # For Logistic regression> install.packages>(>'caTools'>)> # For ROC curve to evaluate model> install.packages>(>'ROCR'>)> > # Loading package> library>(caTools)> library>(ROCR)> |
>
>
Razdelitev podatkov
R
# Splitting dataset> split <->sample.split>(mtcars, SplitRatio = 0.8)> split> train_reg <->subset>(mtcars, split ==>'TRUE'>)> test_reg <->subset>(mtcars, split ==>'FALSE'>)> # Training model> logistic_model <->glm>(vs ~ wt + disp,> >data = train_reg,> >family =>'binomial'>)> logistic_model> # Summary> summary>(logistic_model)> |
>
>
Izhod:
Call: glm(formula = vs ~ wt + disp, family = 'binomial', data = train_reg) Deviance Residuals: Min 1Q Median 3Q Max -1.6552 -0.4051 0.4446 0.6180 1.9191 Coefficients: Estimate Std. Error z value Pr(>|z|) (Prestrezanje) 1,58781 2,60087 0,610 0,5415 teža 1,36958 1,60524 0,853 0,3936 disp -0,02969 0,01577 -1,882 0,0598. --- Signif. kode: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1 (parameter disperzije za binomsko družino je 1) Ničelna deviacija: 34,617 pri 24 prostostnih stopnjah Preostala deviacija: 20,212 pri 22 stopinj svobode AIC: 26.212 Število ponovitev Fisherjevega točkovanja: 6>
- Klic: Prikazan je klic funkcije, uporabljen za prilagajanje logističnemu regresijskemu modelu, skupaj z informacijami o družini, formuli in podatkih. Ostanki odstopanj: To so ostanki odstopanj, ki merijo stopnjo primernosti modela. Pomenijo neskladja med dejanskimi odzivi in verjetnostjo, ki jo napoveduje model logistične regresije. Koeficienti: Ti koeficienti v logistični regresiji predstavljajo log odds ali logit spremenljivke odziva. Standardne napake, povezane z ocenjenimi koeficienti, so prikazane v Std. Stolpec z napakami. Kode pomembnosti: Stopnja pomembnosti vsake spremenljivke napovednika je prikazana s kodami pomembnosti. Disperzijski parameter: V logistični regresiji disperzijski parameter služi kot skalirni parameter za binomsko porazdelitev. V tem primeru je nastavljen na 1, kar pomeni, da je predpostavljena disperzija 1. Ničelno odstopanje: ničelno odstopanje izračuna odstopanje modela, ko se upošteva samo presek. Simbolizira odstopanje, ki bi izhajalo iz modela brez napovednikov. Preostalo odstopanje: Preostalo odstopanje izračuna odstopanje modela po namestitvi napovednikov. Pomeni preostali odklon po upoštevanju napovednikov. AIC: Informacijski kriterij Akaike (AIC), ki upošteva število napovednikov, je merilo ustreznosti modela. Kaznuje bolj zapletene modele, da prepreči prekomerno opremljanje. Bolje prilegajoči modeli so označeni z nižjimi vrednostmi AIC. Število ponovitev Fisherjevega točkovanja: Število ponovitev, ki jih potrebuje postopek Fisherjevega točkovanja za oceno parametrov modela, je označeno s številom ponovitev.
Predvidevanje testnih podatkov na podlagi modela
R
predict_reg <->predict>(logistic_model,> >test_reg, type =>'response'>)> predict_reg> |
>
>
Izhod:
Hornet Sportabout Merc 280C Merc 450SE Chrysler Imperial 0.01226166 0.78972164 0.26380531 0.01544309 AMC Javelin Camaro Z28 Ford Pantera L 0.06104267 0.02807992 0.01107943>
R
java uporabniški vnos
# Changing probabilities> predict_reg <->ifelse>(predict_reg>0,5, 1, 0)>> # Evaluating model accuracy> # using confusion matrix> table>(test_reg$vs, predict_reg)> missing_classerr <->mean>(predict_reg != test_reg$vs)> print>(>paste>(>'Accuracy ='>, 1 - missing_classerr))> # ROC-AUC Curve> ROCPred <->prediction>(predict_reg, test_reg$vs)> ROCPer <->performance>(ROCPred, measure =>'tpr'>,> >x.measure =>'fpr'>)> auc <->performance>(ROCPred, measure =>'auc'>)> auc <- [email protected][[1]]> auc> # Plotting curve> plot>(ROCPer)> plot>(ROCPer, colorize =>TRUE>,> >print.cutoffs.at =>seq>(0.1, by = 0.1),> >main =>'ROC CURVE'>)> abline>(a = 0, b = 1)> auc <->round>(auc, 4)> legend>(.6, .4, auc, title =>'AUC'>, cex = 1)> |
>
>
Izhod:
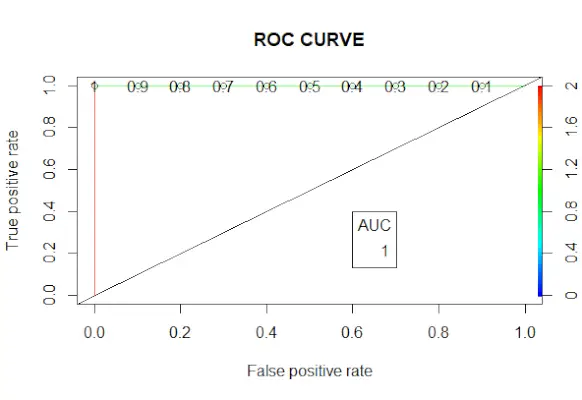
Krivulja ROC
Primer 2:
Izvedemo lahko logistični regresijski model Titanic Data set v R.
R
# Load the dataset> data>(Titanic)> # Convert the table to a data frame> data <->as.data.frame>(Titanic)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # View the summary of the model> summary>(model)> |
>
>
Izhod:
Call: glm(formula = Survived ~ Class + Sex + Age, family = binomial, data = data) Deviance Residuals: Min 1Q Median 3Q Max -1.177 -1.177 0.000 1.177 1.177 Coefficients: Estimate Std. Error z value Pr(>|z|) (Prestrezanje) 4.022e-16 8.660e-01 0 1 Class2nd -9.762e-16 1.000e+00 0 1 Class3rd -4.699e-16 1.000e+00 0 1 ClassCrew -5.551e-16 1.000e+ 00 0 1 SexFemale -3.140e-16 7.071e-01 0 1 AgeAdult 5.103e-16 7.071e-01 0 1 (Disperzijski parameter za binomsko družino velja za 1) Ničelna deviacija: 44,361 pri 31 prostostnih stopinjah Preostala devianca: 44,361 pri 26 stopinjah svobode AIC: 56.361 Število ponovitev Fisherjevega točkovanja: 2>
Narišite krivuljo ROC za nabor podatkov o Titaniku
R
# Install and load the required packages> install.packages>(>'ROCR'>)> library>(ROCR)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # Make predictions on the dataset> predictions <->predict>(model, type =>'response'>)> # Create a prediction object for ROCR> prediction_objects <->prediction>(predictions, titanic_df$Survived)> # Create an ROC curve object> roc_object <->performance>(prediction_obj, measure =>'tpr'>, x.measure =>'fpr'>)> # Plot the ROC curve> plot>(roc_object, main =>'ROC Curve'>, col =>'blue'>, lwd = 2)> # Add labels and a legend to the plot> legend>(>'bottomright'>, legend => >paste>(>'AUC ='>,>round>(>performance>(prediction_objects, measure =>'auc'>)> >@y.values[[1]], 2)), col =>'blue'>, lwd = 2)> |
cimet vs mate
>
>
Izhod:
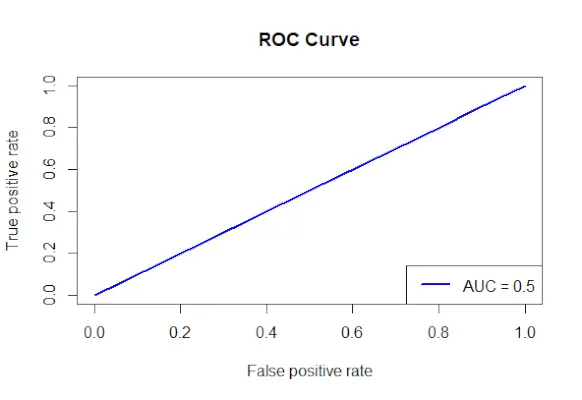
ROC krivulja
- Dejavniki, uporabljeni za napovedovanje preživelih, so določeni, formula preživelih razred + spol + starost pa se uporablja za ustvarjanje logističnega regresijskega modela.
- Z uporabo funkcije predict() se napovedi naredijo za nabor podatkov z uporabo prilagojenega modela.
- Predvidene verjetnosti so združene z dejanskimi vrednostmi izida za izgradnjo objekta napovedi z uporabo metode prediction() iz paketa ROCR.
- Podana je mera prave pozitivne stopnje (tpr) in mera na osi x lažno pozitivne stopnje (fpr), predmet krivulje ROC pa je ustvarjen s funkcijo performance() iz paketa ROCR.
- Objekt krivulje ROC (roc_obj), ki določa glavni naslov, barvo in širino črte, se izriše s funkcijo plot().
- Za določitev vrednosti AUC (površine pod krivuljo) uporablja funkcijo performance() z merami = auc in grafu doda oznake in legendo.
