Linearna regresija in logistična regresija sta dva znana algoritma strojnega učenja, ki spadata pod tehniko nadzorovanega učenja. Ker sta oba algoritma nadzorovane narave, zato ti algoritmi za napovedovanje uporabljajo označeni nabor podatkov. Toda glavna razlika med njimi je, kako se uporabljajo. Linearna regresija se uporablja za reševanje problemov regresije, medtem ko se logistična regresija uporablja za reševanje problemov klasifikacije. Opis obeh algoritmov je podan spodaj skupaj s tabelo razlik.
Linearna regresija:
- Linearna regresija je eden najpreprostejših algoritmov strojnega učenja, ki spada pod tehniko nadzorovanega učenja in se uporablja za reševanje regresijskih problemov.
- Uporablja se za napovedovanje zvezne odvisne spremenljivke s pomočjo neodvisnih spremenljivk.
- Cilj linearne regresije je najti črto, ki se najbolje prilega, ki lahko natančno napove izhod za neprekinjeno odvisno spremenljivko.
- Če se za napoved uporablja ena sama neodvisna spremenljivka, se to imenuje enostavna linearna regresija, če pa obstaja več kot dve neodvisni spremenljivki, se taka regresija imenuje večkratna linearna regresija.
- Z iskanjem najprimernejše črte algoritem vzpostavi razmerje med odvisno spremenljivko in neodvisno spremenljivko. In razmerje mora biti linearne narave.
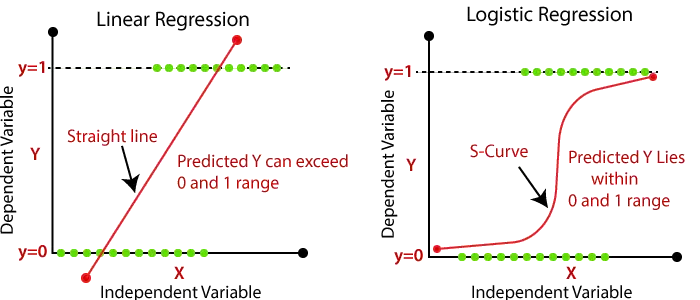
- Izhod za linearno regresijo bi morale biti le zvezne vrednosti, kot so cena, starost, plača itd. Razmerje med odvisno spremenljivko in neodvisno spremenljivko je lahko prikazano na spodnji sliki:

Na zgornji sliki je odvisna spremenljivka na osi Y (plača), neodvisna spremenljivka pa na osi x (izkušnje). Regresijsko črto lahko zapišemo kot:
y= a<sub>0</sub>+a<sub>1</sub>x+ ε
Kje0in a1so koeficienti in ε je člen napake.
Logistična regresija:
- Logistična regresija je eden najbolj priljubljenih algoritmov strojnega učenja, ki spada pod tehnike nadzorovanega učenja.
- Uporablja se lahko za klasifikacijske in regresijske probleme, vendar se uporablja predvsem za klasifikacijske probleme.
- Logistična regresija se uporablja za napovedovanje kategorične odvisne spremenljivke s pomočjo neodvisnih spremenljivk.
- Rezultat problema logistične regresije je lahko samo med 0 in 1.
- Logistično regresijo je mogoče uporabiti, kadar se zahtevajo verjetnosti med dvema razredoma. Na primer, ali bo danes deževalo ali ne, 0 ali 1, res ali napačno itd.
- Logistična regresija temelji na konceptu ocene največje verjetnosti. Po tej oceni naj bi bili opaženi podatki najbolj verjetni.
- Pri logistični regresiji posredujemo tehtano vsoto vnosov skozi aktivacijsko funkcijo, ki lahko preslika vrednosti med 0 in 1. Takšna aktivacijska funkcija je znana kot sigmoidno funkcijo in dobljeno krivuljo imenujemo sigmoidna krivulja ali S-krivulja. Razmislite o spodnji sliki:

- Enačba za logistično regresijo je:

Razlika med linearno regresijo in logistično regresijo:
| Linearna regresija | Logistična regresija |
|---|---|
| Linearna regresija se uporablja za napovedovanje zvezne odvisne spremenljivke z uporabo danega niza neodvisnih spremenljivk. | Logistična regresija se uporablja za napovedovanje kategorične odvisne spremenljivke z uporabo danega niza neodvisnih spremenljivk. |
| Linearna regresija se uporablja za reševanje problema regresije. | Logistična regresija se uporablja za reševanje problemov klasifikacije. |
| Pri linearni regresiji napovemo vrednost zveznih spremenljivk. | V logistični regresiji napovemo vrednosti kategoričnih spremenljivk. |
| Pri linearni regresiji najdemo najbolj prilegajočo se črto, po kateri lahko enostavno napovemo izhod. | Pri logistični regresiji najdemo S-krivuljo, po kateri lahko razvrstimo vzorce. |
| Za oceno točnosti se uporablja metoda najmanjšega kvadrata. | Za oceno točnosti se uporablja metoda ocene največje verjetnosti. |
| Rezultat za linearno regresijo mora biti zvezna vrednost, kot je cena, starost itd. | Rezultat logistične regresije mora biti kategorična vrednost, kot je 0 ali 1, Da ali Ne itd. |
| Pri linearni regresiji se zahteva, da mora biti razmerje med odvisno in neodvisno spremenljivko linearno. | Pri logistični regresiji ni zahtevana linearna povezava med odvisno in neodvisno spremenljivko. |
| Pri linearni regresiji lahko pride do kolinearnosti med neodvisnimi spremenljivkami. | Pri logistični regresiji ne sme biti kolinearnosti med neodvisno spremenljivko. |
