Linearno programiranje je matematični koncept, ki se uporablja za iskanje optimalne rešitve linearne funkcije. Ta metoda uporablja preproste predpostavke za optimizacijo dane funkcije. Linearno programiranje ima ogromno aplikacij v resničnem svetu in se uporablja za reševanje različnih vrst problemov.
Linearno programiranje se uporablja v različnih panogah, kot so ladjarska industrija, proizvodna industrija, transportna industrija, telekomunikacije in druge.
Izraz linearno programiranje je sestavljen iz dveh besed linearno in programiranje, beseda linearno pove razmerje med različnimi vrstami spremenljivk stopnje ena, uporabljenih v problemu, beseda programiranje pa nam pove postopek po korakih za reševanje teh problemov.
V tem članku bomo podrobno spoznali linearno programiranje, njegove primere, formule in druge koncepte.
Kazalo
- Kaj je linearno programiranje?
- Komponente linearnega programiranja
- Primeri linearnega programiranja
- Težave z linearnim programiranjem
- Vrste problemov linearnega programiranja
- Formula linearnega programiranja
- Kako rešiti probleme linearnega programiranja?
- Metode linearnega programiranja
- Simpleksna metoda linearnega programiranja
- Grafična metoda linearnega programiranja
- Aplikacije za linearno programiranje
- Pomen linearnega programiranja
- Najsodobnejše aplikacije linearnega programiranja
- Linearno programiranje v operacijskih raziskavah
- Simpleksna metoda
Kaj je linearno programiranje?
Linearno programiranje oz Linearna optimizacija je tehnika, ki nam pomaga najti optimalno rešitev za dano težavo, optimalna rešitev je rešitev, ki je najboljši možni izid določenega problema.
Preprosto povedano, to je metoda, s katero ugotovimo, kako nekaj narediti na najboljši možni način. Z omejenimi viri morate zagotoviti optimalno uporabo virov in doseči najboljši možni rezultat pri določenem cilju, kot so najmanjši stroški, najvišja marža ali najkrajši čas.
Situacija, ki zahteva iskanje najboljših vrednosti spremenljivk ob upoštevanju določenih omejitev, je tam, kjer uporabljamo probleme linearnega programiranja. Teh situacij ni mogoče rešiti z običajnimi računskimi in numeričnimi tehnikami.
Definicija linearnega programiranja
Linearno programiranje je tehnika, ki se uporablja za optimizacijo določenega scenarija. Uporaba linearnega programiranja nam zagotavlja najboljši možni rezultat v dani situaciji. Uporablja vse razpoložljive vire na način, ki daje optimalen rezultat.
Komponente linearnega programiranja
Osnovne komponente problema linearnega programiranja (LP) so:
- Odločitvene spremenljivke: Spremenljivke, ki jih želite določiti, da dosežete optimalno rešitev.
- Ciljna funkcija: M atematična enačba, ki predstavlja cilj, ki ga želite doseči
- Omejitve: Omejitve ali omejitve, ki jim morajo slediti vaše odločitvene spremenljivke.
- Omejitve brez negativnosti: V nekaterih v realnem svetu spremenljivke odločitve ne morejo biti negativne
Dodatne značilnosti linearnega programiranja
- Končnost: Število odločitvenih spremenljivk in omejitev v problemu LP je končno.
- Linearnost: Ciljna funkcija in vse omejitve morajo biti linearne funkcije odločitvenih spremenljivk . To pomeni, da mora biti stopnja spremenljivk ena.
Primeri linearnega programiranja
Situacije, v katerih se uporablja linearno programiranje, lahko razumemo s pomočjo primera, obravnavanega spodaj,
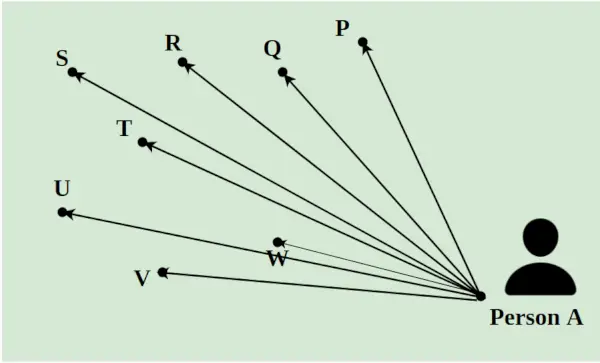
Recimo, da mora dostavljavec dostaviti 8 paketov na dan na različne lokacije v mestu. Izbrati mora vse pakete iz A in jih dostaviti do točk P, Q, R, S, T, U, V in W. Razdalja med njimi je označena s črtami, kot je prikazano na spodnji sliki. Najkrajša pot, ki ji sledi dostavljalec, je izračunana s konceptom linearnega programiranja.
nepodpisano programiranje int c
Težave z linearnim programiranjem
Težave z linearnim programiranjem (LPP) vključujejo optimizacijo linearne funkcije, da bi našli optimalno vrednostno rešitev za funkcijo. Optimalna vrednost je lahko največja ali najmanjša vrednost.
V LPP se imenujejo linearne funkcije objektivne funkcije. Ciljna funkcija ima lahko več spremenljivk, ki so podvržene pogojem in morajo izpolnjevati linearne omejitve .
Vrste problemov linearnega programiranja
Obstaja veliko različnih problemov linearnega programiranja (LPP), vendar bomo v tem članku obravnavali tri glavne probleme linearnega programiranja.
Težave pri izdelavi
Težave v proizvodnji so problem, ki se ukvarja s številom enot, ki jih je treba proizvesti ali prodati, da bi povečali dobiček, ko vsak izdelek zahteva stalno delovno silo, strojne ure in surovine.
Težave s prehrano
Uporablja se za izračun števila različnih vrst sestavin, ki jih je treba vključiti v prehrano, da bi dosegli minimalne stroške, odvisno od razpoložljivosti živil in njihovih cen.
Težave s prevozom
Uporablja se za določitev razporeda prevoza, da bi našli najcenejši način prevoza izdelka iz obratov/tovarn, ki se nahajajo na različnih lokacijah, na različne trge.
Formula linearnega programiranja
Problem linearnega programiranja je sestavljen iz
- Odločitvene spremenljivke
- Ciljna funkcija
- Omejitve
- Negativne omejitve
Odločitvene spremenljivke sta spremenljivki x in y, ki odločata o rezultatu problema linearnega programiranja in predstavljata končno rešitev.
The objektivna funkcija , ki jo na splošno predstavlja Z, je linearna funkcija, ki jo je treba optimizirati glede na dani pogoj, da dobimo končno rešitev.
The omejitve naložene spremenljivkam odločitve, ki omejujejo njihove vrednosti, se imenujejo omejitve.
Splošna formula problema linearnega programiranja je,
Ciljna funkcija : Z = sekira + stran
Omejitve: cx + dy ≥ e, px + qy ≤ r
Negativne omejitve: x ≥ 0, y ≥ 0
V zgornjem pogoju sta x in y spremenljivki odločitve.
Kako rešiti probleme linearnega programiranja?
Preden rešimo probleme linearnega programiranja, jih moramo najprej formulirati glede na standardne parametre. Koraki za reševanje problemov linearnega programiranja so:
Korak 1: Označite odločitvene spremenljivke v problemu.
2. korak: Zgradite ciljno funkcijo problema in preverite, ali je treba funkcijo minimizirati ali maksimirati.
3. korak: Zapišite vse omejitve linearnih problemov.
4. korak: Zagotovite nenegativne omejitve spremenljivk odločitve.
5. korak: Zdaj rešite problem linearnega programiranja s katero koli metodo, običajno uporabljamo bodisi simpleksno ali grafično metodo.
Metode linearnega programiranja
Za reševanje problemov linearnega programiranja uporabljamo različne metode. Dve najpogostejši uporabljeni metodi sta,
- Simpleksna metoda
- Grafična metoda
Spoznajmo ti dve metodi podrobno v tem članku,
Simpleksna metoda linearnega programiranja
Ena najpogostejših metod za reševanje problema linearnega programiranja je metoda simpleksa. Pri tej metodi določen pogoj 'n' večkrat ponovimo, dokler ne dosežemo optimalne rešitve.
Koraki, potrebni za reševanje problemov linearnega programiranja z uporabo metode simpleksa, so:
Korak 1: Formulirajte probleme linearnega programiranja na podlagi danih omejitev.
2. korak: Pretvorite vse dane neenakosti v enačbe ali enačbe problemov linearnega programiranja tako, da vsaki neenakosti dodate spremenljivko slack, kjer je to potrebno.
3. korak: Sestavite začetno simpleks tabelo. S predstavitvijo vsake omejitvene enačbe v vrstici in pisanjem ciljne funkcije v spodnjo vrstico. Tako dobljeno tabelo imenujemo Simplex tabela.
4. korak: Identificirajte največji negativni vnos v spodnji vrstici, stolpec elementa z najvišjim negativnim vnosom se imenuje vrtilni stolpec
5. korak: Vnose v skrajno desnem stolpcu razdelite z vnosi v ustreznem vrtilnem stolpcu, pri čemer izključite vnose v skrajni spodnji vrstici. Zdaj se vrstica, ki vsebuje najmanj vnosa, imenuje vrtilna vrstica. Vrtilni element dobimo s presekom vrtilne vrstice in vrtilnega stolpca.
6. korak: Z uporabo matrične operacije in s pomočjo vrtilnega elementa naredite vse vnose v vrtilnem stolpcu enake nič.
7. korak: Preverite nenegativne vnose v skrajni spodnji vrstici, če v spodnji vrstici ni negativnih vnosov, končajte postopek, drugače začnite postopek znova od 4. koraka.
8. korak: Tako dobljena končna preprosta tabela daje rešitev našega problema.
Grafična metoda linearnega programiranja
Grafična metoda je druga metoda kot metoda Simplex, ki se uporablja za reševanje problemov linearnega programiranja. Kot že ime pove, ta metoda uporablja grafe za reševanje danih problemov linearnega programiranja. To je najboljša metoda za reševanje problemov linearnega programiranja in zahteva manj truda kot metoda simpleksa.
Pri uporabi te metode narišemo vse neenakosti, ki so podvržene omejitvam v danih problemih linearnega programiranja. Takoj, ko so vse neenačbe danega LPP narisane na grafu XY, skupno območje vseh neenačb daje optimalno rešitev. Izračunamo vse kotne točke izvedljive regije in izračunamo vrednost ciljne funkcije na vseh teh točkah, nato pa s primerjavo teh vrednosti dobimo optimalno rešitev LPP.
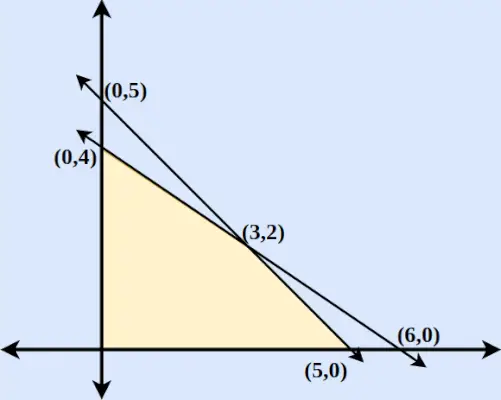
Primer: Poiščite največjo in najmanjšo vrednost z = 6x + 9y, ko so pogoji omejitve:
- 2x + 3y ≤ 12
- x in y ≥ 0
- x + y ≤ 5
rešitev:
Korak 1 : Najprej pretvorite neenačbe v normalne enačbe. Zato bodo enačbe 2x+3y = 0, x = 0, y = 0 in x + y = 5.
2. korak : Poiščite točke, v katerih 2x + 3y in x + y = 5 sekata os x in y. Če želite najti presečišče osi x, vstavite y = 0 v ustrezno enačbo in poiščite točko. Podobno za točke presečišča osi y vstavite x = 0 v ustrezno enačbo.
3. korak : Narišite dve črti, ki sekata os x in y. Ugotovimo, da se obe osi medsebojno sekata pri (3,2).
4. korak : Za x ≥ 0 in y ≥ 0 ugotovimo, da sta upoštevani obe neenačbi. Zato bo regija vključevala območje območja, ki ga obdajata dve ose in obe črti, vključno z izhodiščem. Izrisano območje je prikazano na spodnji sliki.
5. korak : Poiščite Z za vsako točko ter maksimume in minimume.
Koordinate Z = 6x + 9y (0,5) Z = 45 (0,4) Z = 36 (5,0) Z = 30 (6,0) Z = 36 (3,2) Z = 36 Zato ugotovimo, da je Z = 6x + 9y največji pri (0,5) in najmanjši pri (5,0).
Aplikacije za linearno programiranje
Linearno programiranje se uporablja na različnih področjih. Uporablja se za iskanje minimalnih stroškov postopka, ko so podane vse omejitve težav. Uporablja se za optimizacijo stroškov prevoza vozila itd. Različne aplikacije linearnega programiranja so
Inženirska industrija
Engineering Industries uporablja linearno programiranje za reševanje projektnih in proizvodnih problemov ter za doseganje največjega rezultata iz danih pogojev.
Predelovalne industrije
Proizvodne industrije uporabljajo linearno programiranje za povečanje dobička podjetij in zmanjšanje proizvodnih stroškov.
Energetske industrije
Energetska podjetja uporabljajo linearno programiranje za optimizacijo proizvodnje.
Transportne industrije
Linearno programiranje se uporablja tudi v transportnih panogah za iskanje poti za zmanjšanje stroškov transporta.
Pomen linearnega programiranja
Linearno programiranje ima velik pomen v različnih panogah, saj maksimira izhodno vrednost, hkrati pa zmanjša vhodne vrednosti glede na različne omejitve.
LP je zelo uporaben, ko imamo med reševanjem problema več pogojev in moramo optimizirati rezultat problema, tj. najti moramo najmanjšo ali največjo vrednost glede na dani pogoj.
Preberi več,
- Linearne neenakosti
- Algebraična rešitev linearnih neenačb
Težave z linearnim programiranjem
Problem 1: Podjetje proizvaja in prodaja dve vrsti izdelkov in stroški proizvodnje vsake enote a in b so 200 oziroma 150 rupij, vsaka enota izdelka prinese dobiček 20 rupij in vsaka enota izdelka b prinese dobiček 15 rupij pri prodaji. . Družba ocenjuje, da je mesečno povpraševanje A in B največ požeta enota v celotnem proizvodnem proračunu za mesec, ki je nastavljen na 50000 rupij. Koliko enot bi moralo podjetje proizvesti, da bi zaslužilo največji dobiček od svoje mesečne prodaje iz in b?
rešitev:
Naj bo x = število enot vrste A
y = število enot tipa B
Povečajte Z = 40x + 50y
Ob upoštevanju omejitev
3x + y ≤ 9
x + 2y ≤ 8
in x, y ≥ 0
Razmislite o enačbi,
3x + y = 9
x = 3
y = 0
in x + 2y = 8
java dodaj v matrikox = 8
y = 0
Zdaj lahko določimo največjo vrednost Z z vrednotenjem vrednosti Z na štirih točkah (točkah), ki so prikazane spodaj
Oglišča
Z = 40x + 50y
(0, 0)
Z = 40 × 0 + 50 × 0 = Rs. 0
(3, 0)
Z = 40 × 3 + 50 × 0 = Rs. 120
(0, 4)
Z = 40 × 0 + 50 × 4 = Rs. 200
(23)
Z = 40 × 2 + 50 × 3 = Rs. 230
Največji dobiček, Z = Rs. 230
∴ Število enot tipa A je 2, število enot tipa B pa 3.
Problem 2: Maksimiraj Z = 3x + 4y.
Ob upoštevanju omejitev, x + y ≤ 450, 2x + y ≤ 600 in x, y ≤ 0.
rešitev:
Imamo iz danega
Omejitve (1)
X + Y = 450
Če damo x = 0, ⇒ 0 + y = 450 ⇒ y = 450
Če damo y = 0, ⇒ x + 0 = 450 ⇒ x = 450
od, Omejitve (2)
2x + y = 600
Če postavimo x = 0, ⇒ 0 + y = 600 ⇒ y = 600
Če postavimo y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300
Zdaj imamo koordinato točk Z = 3x + 4y
| Oglišča | Z = 3x + 4y |
|---|---|
| (0, 0) | Z = 3 × 0 + 4 × 0 = 0 |
| (300, 0) | Z = 3 × 300 + 4 × 0 = 900 |
| (150, 300) | Z = 3 × 150 + 4 × 300 = 1650 |
| (0, 450) | Z = 3 × 0 + 4 × 450 = 1800 |
Zato je optimalna rešitev največ Z = 1800 na koordinati x = 0 in y = 450. Graf je podan spodaj.

Najsodobnejše aplikacije linearnega programiranja
Linearno programiranje, zmogljiva matematična tehnika, se uporablja za reševanje problemov optimizacije v različnih panogah. Tukaj je nekaj sodobnih aplikacij:
- Optimizacija dobavne verige : Linearno programiranje pomaga podjetjem zmanjšati stroške in povečati učinkovitost v svojih dobavnih verigah. Uporablja se za določanje stroškovno najučinkovitejših transportnih poti, skladiščnih operacij in strategij upravljanja zalog.
- Upravljanje z energijo : V energetskem sektorju se linearno programiranje uporablja za optimizacijo mešanice metod proizvodnje energije. To vključuje uravnoteženje tradicionalnih virov energije z obnovljivimi viri, da se zmanjšajo stroški in vpliv na okolje ter hkrati zadosti povpraševanju.
- Načrtovanje telekomunikacijskega omrežja : Linearno programiranje pomaga pri načrtovanju učinkovitih telekomunikacijskih omrežij. Pomaga pri dodeljevanju pasovne širine, načrtovanju omrežnih postavitev in optimiziranju pretoka podatkov, da se zagotovi hitra komunikacija z nižjimi stroški.
- Finančno načrtovanje : Podjetja in finančni analitiki uporabljajo linearno programiranje za optimizacijo portfelja, obvladovanje tveganja in načrtovanje kapitala. Pomaga pri sprejemanju naložbenih odločitev, ki maksimirajo donose in hkrati zmanjšajo tveganje.
- Zdravstvena logistika : V zdravstvu se linearno programiranje uporablja za optimizacijo dodeljevanja virov, kot so bolnišnične postelje, medicinsko osebje in oprema. To je ključnega pomena za izboljšanje oskrbe bolnikov, skrajšanje čakalnih dob in učinkovito upravljanje stroškov.
- Optimizacija proizvodnega procesa : Linearno programiranje se uporablja za določanje optimalnih ravni proizvodnje za več izdelkov v proizvodnem obratu, pri čemer se upoštevajo omejitve, kot so delovna sila, materiali in razpoložljivost strojev.
- Načrtovanje kmetijstva : Kmetje in kmetijski načrtovalci uporabljajo linearno programiranje za odločanje o izbiri pridelkov, rabi zemlje in razporeditvi virov, da povečajo donos in dobiček ob ohranjanju virov.
- Razpored letalskih posadk : Letalske družbe uporabljajo linearno programiranje za učinkovito razporejanje posadk, s čimer zagotavljajo, da je osebje na letih v skladu s predpisi, in zmanjšujejo operativne stroške.
Te aplikacije prikazujejo vsestranskost in moč linearnega programiranja pri reševanju zapletenih problemov optimizacije v različnih sektorjih, kar kaže na njegovo pomembnost v današnjem svetu, ki temelji na podatkih.
Linearno programiranje v operacijskih raziskavah
- Osnovno orodje : Linearno programiranje je temeljno orodje v operacijskih raziskavah za optimizacijo virov.
- Odločanje : Pomaga pri sprejemanju najboljših odločitev glede dodeljevanja virov, maksimiranja dobička ali minimiziranja stroškov.
- Široke aplikacije : Uporablja se na različnih področjih, kot so logistika, proizvodnja, finance in zdravstvo za reševanje kompleksnih problemov.
- Modeliranje problemov iz resničnega sveta : Preoblikuje probleme iz resničnega sveta v matematične modele za iskanje najučinkovitejših rešitev.
Simpleksna metoda
- Optimizacijski algoritem : Metoda Simplex je zmogljiv algoritem, ki se uporablja v linearnem programiranju za iskanje optimalne rešitve linearnih neenakosti.
- Pristop po korakih : Iterativno se pomika proti najboljši rešitvi s krmarjenjem po robovih izvedljivega območja, opredeljenega z omejitvami.
- Učinkovitost : znan po svoji učinkovitosti pri reševanju obsežnih problemov linearnega programiranja.
- Vsestranskost : Uporabno na različnih področjih, kot so načrtovanje prehrane, omrežni tokovi, načrtovanje proizvodnje in več, s prikazom svoje vsestranskosti.
Linearno programiranje – pogosta vprašanja
Kaj je linearno programiranje?
Linearno programiranje je matematični koncept, ki se uporablja za optimizacijo danega linearnega problema, ki ima različne omejitve. Z linearnim programiranjem dobimo optimalen rezultat danega problema
Kaj so težave z linearnim programiranjem?
Problemi linearnega programiranja (LPP) so problemi, ki dajejo optimalno rešitev danih pogojev.
Kaj je formula linearnega programiranja?
Splošne formule linearnega programiranja so,
- Ciljna funkcija: Z = ax + by
- Omejitve: px + qy ≤ r, sx + ty ≤ u
- Nenegativne omejitve: x ≥ 0, y ≥ 0
Katere so različne vrste linearnega programiranja?
Različne vrste metod linearnega programiranja so,
- Linearno programiranje po Simpleksni metodi
- Linearno programiranje z metodo R
- Linearno programiranje z grafično metodo
Kakšne so zahteve za linearno programiranje?
Različne zahteve problemov linearnega programiranja so,
- Linearnost
- Ciljna funkcija
- Omejitve
- Nenegativnost
Kakšne so prednosti linearnega programiranja?
Različne prednosti linearnega programiranja so,
- Zagotavlja optimalno rešitev za vsak dani linearni problem.
- Je enostaven za uporabo in vedno daje dosledne rezultate
- Pomaga povečati dobiček in zmanjšati vhodne stroške.