logo

TechCodeview

Največje število v BST, ki je manjše ali enako k

Glede na koren a Binarno iskalno drevo in celo število k . Naloga je najti največje število v binarnem iskalnem drevesu, to je manj kot oz enaka na k, če tak element ne obstaja, natisni -1. 

Primeri:  

Vnos:



Največje-število-v-BST-ki-je-manjše-ali-enako-k-1' title=

Izhod: 21
Pojasnilo: 19 in 25 sta dve najbližji števili 21 in 19 je največje število, ki ima vrednost manjšo ali enako 21.

Vnos: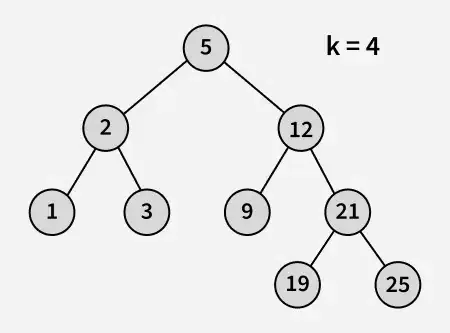

Največje-število-v-BST-ki-je-manjše-ali-enako-k-2' loading='lazy' title=

Izhod: 3
Pojasnilo: 3 in 5 sta dve najbližji števili 4 in 3 je največje število, ki ima vrednost manjšo ali enako 4.

Kazalo vsebine

[Naivni pristop] Uporaba rekurzije - O(h) čas in O(h) prostor

Ideja je začeti pri korenina in primerjajte njegovo vrednost s k. Če je vrednost vozlišča večja od k, se pomaknite na levo poddrevo. V nasprotnem primeru poiščite vrednost največjega števila, manjšega od k v desno poddrevo . Če desno poddrevo vrne -1 (kar pomeni, da taka vrednost ne obstaja), vrne vrednost trenutnega vozlišča. Drugače vrne vrednost, ki jo vrne desno poddrevo (ker bo večja od vrednosti trenutnega vozlišča, vendar manj kot enaka k).

C++ 
// C++ code to find the largest value  // smaller than or equal to k using recursion #include    using namespace std; class Node { public:  int data;  Node *left *right;    Node(int val){  data = val;  left = nullptr;  right = nullptr;  } }; // function to find max value less than k int findMaxFork(Node* root int k) {    // Base cases  if (root == nullptr)  return -1;  if (root->data == k)  return k;  // If root's value is smaller  // try in right subtree  else if (root->data < k) {    int x = findMaxFork(root->right k);  if (x == -1)  return root->data;  else  return x;  }  // If root's data is greater   // return value from left subtree.  return findMaxFork(root->left k);  } int main() {    int k = 24;  // creating following BST  //  // 5  // /    // 2 12  // /  /    // 1 3 9 21  // /    // 19 25  Node* root = new Node(5);  root->left = new Node(2);  root->left->left = new Node(1);  root->left->right = new Node(3);  root->right = new Node(12);  root->right->left = new Node(9);  root->right->right = new Node(21);  root->right->right->left = new Node(19);  root->right->right->right = new Node(25);    cout << findMaxFork(root k);  return 0; }
Java 
// Java code to find the largest value  // smaller than or equal to k using recursion class Node {  int data;  Node left right;    Node(int val) {  data = val;  left = null;  right = null;  } } class GfG {    // function to find max value less than k  static int findMaxFork(Node root int k) {    // Base cases  if (root == null)  return -1;  if (root.data == k)  return k;  // If root's value is smaller  // try in right subtree  else if (root.data < k) {  int x = findMaxFork(root.right k);  if (x == -1)  return root.data;  else  return x;  }  // If root's data is greater  // return value from left subtree.  return findMaxFork(root.left k);  }  public static void main(String[] args) {  int k = 24;  // creating following BST  //  // 5  // /    // 2 12  // /  /    // 1 3 9 21  // /    // 19 25  Node root = new Node(5);  root.left = new Node(2);  root.left.left = new Node(1);  root.left.right = new Node(3);  root.right = new Node(12);  root.right.left = new Node(9);  root.right.right = new Node(21);  root.right.right.left = new Node(19);  root.right.right.right = new Node(25);  System.out.println(findMaxFork(root k));  } }
Python 
# Python code to find the largest value  # smaller than or equal to k using recursion class Node: def __init__(self val): self.data = val self.left = None self.right = None # function to find max value less than k def findMaxFork(root k): # Base cases if root is None: return -1 if root.data == k: return k # If root's value is smaller # try in right subtree elif root.data < k: x = findMaxFork(root.right k) if x == -1: return root.data else: return x # If root's data is greater # return value from left subtree. return findMaxFork(root.left k) if __name__ == '__main__': k = 24 # creating following BST # # 5 # /   # 2 12 # /  /   # 1 3 9 21 # /   # 19 25 root = Node(5) root.left = Node(2) root.left.left = Node(1) root.left.right = Node(3) root.right = Node(12) root.right.left = Node(9) root.right.right = Node(21) root.right.right.left = Node(19) root.right.right.right = Node(25) print(findMaxFork(root k))
C# 
// C# code to find the largest value  // smaller than or equal to k using recursion using System; class Node {  public int data;  public Node left right;    public Node(int val) {  data = val;  left = null;  right = null;  } } class GfG {    // function to find max value less than k  static int FindMaxFork(Node root int k) {    // Base cases  if (root == null)  return -1;  if (root.data == k)  return k;  // If root's value is smaller  // try in right subtree  else if (root.data < k) {  int x = FindMaxFork(root.right k);  if (x == -1)  return root.data;  else  return x;  }  // If root's data is greater  // return value from left subtree.  return FindMaxFork(root.left k);  }  static void Main() {  int k = 24;  // creating following BST  //  // 5  // /    // 2 12  // /  /    // 1 3 9 21  // /    // 19 25  Node root = new Node(5);  root.left = new Node(2);  root.left.left = new Node(1);  root.left.right = new Node(3);  root.right = new Node(12);  root.right.left = new Node(9);  root.right.right = new Node(21);  root.right.right.left = new Node(19);  root.right.right.right = new Node(25);  Console.WriteLine(FindMaxFork(root k));  } }
JavaScript 
// JavaScript code to find the largest value  // smaller than or equal to k using recursion class Node {  constructor(val) {  this.data = val;  this.left = null;  this.right = null;  } } // function to find max value less than k function findMaxFork(root k) {    // Base cases  if (root === null)  return -1;  if (root.data === k)  return k;  // If root's value is smaller  // try in right subtree  else if (root.data < k) {  let x = findMaxFork(root.right k);  if (x === -1)  return root.data;  else  return x;  }  // If root's data is greater  // return value from left subtree.  return findMaxFork(root.left k); } let k = 24; // creating following BST // // 5 // /   // 2 12 // /  /   // 1 3 9 21 // /   // 19 25 let root = new Node(5); root.left = new Node(2); root.left.left = new Node(1); root.left.right = new Node(3); root.right = new Node(12); root.right.left = new Node(9); root.right.right = new Node(21); root.right.right.left = new Node(19); root.right.right.right = new Node(25); console.log(findMaxFork(root k));

Izhod 
21

[Pričakovan pristop] Uporaba iteracije - O(h) čas in O(1) prostor

Ideja je začeti pri korenina in primerjajte njegovo vrednost z k . Če je vrednost vozlišča <= k posodobi rezultat rezultata na korensko vrednost in se premakni na desno poddrevo se premakne v levo poddrevo. Avtor: iterativno z uporabo te operacije v vseh vozliščih lahko zmanjšamo prostor, potreben za rekurzija kup.

C++ 
// C++ code to find the largest value  // smaller than or equal to k using recursion #include    using namespace std; class Node { public:  int data;  Node *left *right;    Node(int val){  data = val;  left = nullptr;  right = nullptr;  } }; // function to find max value less than k int findMaxFork(Node* root int k) {    int result = -1;    // Start from root and keep looking for larger   while (root != nullptr) {  // If root is smaller go to right side  if (root->data <= k){  result = root->data;  root = root->right;  }  // If root is greater go to left side   else  root = root->left;  }    return result; } int main() {    int k = 24;  // creating following BST  //  // 5  // /    // 2 12  // /  /    // 1 3 9 21  // /    // 19 25  Node* root = new Node(5);  root->left = new Node(2);  root->left->left = new Node(1);  root->left->right = new Node(3);  root->right = new Node(12);  root->right->left = new Node(9);  root->right->right = new Node(21);  root->right->right->left = new Node(19);  root->right->right->right = new Node(25);    cout << findMaxFork(root k);  return 0; }
Java 
// Java code to find the largest value  // smaller than or equal to k using recursion class Node {  int data;  Node left right;    Node(int val) {  data = val;  left = null;  right = null;  } } class GfG {    // function to find max value less than k  static int findMaxFork(Node root int k) {  int result = -1;    // Start from root and keep looking for larger   while (root != null) {  // If root is smaller go to right side  if (root.data <= k) {  result = root.data;  root = root.right;  }  // If root is greater go to left side   else {  root = root.left;  }  }    return result;  }  public static void main(String[] args) {  int k = 24;  // creating following BST  //  // 5  // /    // 2 12  // /  /    // 1 3 9 21  // /    // 19 25  Node root = new Node(5);  root.left = new Node(2);  root.left.left = new Node(1);  root.left.right = new Node(3);  root.right = new Node(12);  root.right.left = new Node(9);  root.right.right = new Node(21);  root.right.right.left = new Node(19);  root.right.right.right = new Node(25);  System.out.println(findMaxFork(root k));  } }
Python 
# Python code to find the largest value  # smaller than or equal to k using recursion class Node: def __init__(self val): self.data = val self.left = None self.right = None # function to find max value less than k def findMaxFork(root k): result = -1 # Start from root and keep looking for larger  while root is not None: # If root is smaller go to right side if root.data <= k: result = root.data root = root.right # If root is greater go to left side  else: root = root.left return result if __name__ == '__main__': k = 24 # creating following BST # # 5 # /   # 2 12 # /  /   # 1 3 9 21 # /   # 19 25 root = Node(5) root.left = Node(2) root.left.left = Node(1) root.left.right = Node(3) root.right = Node(12) root.right.left = Node(9) root.right.right = Node(21) root.right.right.left = Node(19) root.right.right.right = Node(25) print(findMaxFork(root k))
C# 
// C# code to find the largest value  // smaller than or equal to k using recursion using System; class Node {  public int data;  public Node left right;    public Node(int val) {  data = val;  left = null;  right = null;  } } class GfG {    // function to find max value less than k  static int FindMaxFork(Node root int k) {  int result = -1;    // Start from root and keep looking for larger   while (root != null) {  // If root is smaller go to right side  if (root.data <= k) {  result = root.data;  root = root.right;  }  // If root is greater go to left side   else {  root = root.left;  }  }    return result;  }  static void Main() {  int k = 24;  // creating following BST  //  // 5  // /    // 2 12  // /  /    // 1 3 9 21  // /    // 19 25  Node root = new Node(5);  root.left = new Node(2);  root.left.left = new Node(1);  root.left.right = new Node(3);  root.right = new Node(12);  root.right.left = new Node(9);  root.right.right = new Node(21);  root.right.right.left = new Node(19);  root.right.right.right = new Node(25);  Console.WriteLine(FindMaxFork(root k));  } }
JavaScript 
// JavaScript code to find the largest value  // smaller than or equal to k using recursion class Node {  constructor(val) {  this.data = val;  this.left = null;  this.right = null;  } } // function to find max value less than k function findMaxFork(root k) {  let result = -1;    // Start from root and keep looking for larger   while (root !== null) {  // If root is smaller go to right side  if (root.data <= k) {  result = root.data;  root = root.right;  }  // If root is greater go to left side   else {  root = root.left;  }  }    return result; } let k = 24; // creating following BST // // 5 // /   // 2 12 // /  /   // 1 3 9 21 // /   // 19 25 let root = new Node(5); root.left = new Node(2); root.left.left = new Node(1); root.left.right = new Node(3); root.right = new Node(12); root.right.left = new Node(9); root.right.right = new Node(21); root.right.right.left = new Node(19); root.right.right.right = new Node(25); console.log(findMaxFork(root k));

Izhod 
21
Ustvari kviz