Končni avtomat (FA) je najpreprostejši stroj za prepoznavanje vzorcev. Uporablja se za karakterizacijo običajnega jezika, na primer: /baa+!/.
Uporablja se tudi za analizo in prepoznavanje izrazov naravnega jezika. Končni avtomat ali končni avtomat je abstrakten stroj, ki ima pet elementov ali tupl. Ima nabor stanj in pravil za premikanje iz enega stanja v drugo, vendar je odvisno od uporabljenega vhodnega simbola. Na podlagi stanj in nabora pravil se lahko vhodni niz sprejme ali zavrne. V bistvu gre za abstrakten model digitalnega računalnika, ki prebere vhodni niz in spremeni svoje notranje stanje glede na trenutni vhodni simbol. Vsak avtomat definira jezik, tj. niz nizov, ki jih sprejema. Naslednja slika prikazuje nekatere bistvene značilnosti splošne avtomatizacije.
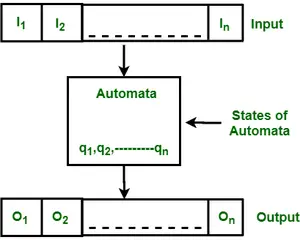
Slika: Značilnosti končnih avtomatov
Zgornja slika prikazuje naslednje značilnosti avtomatov:
- Vnos
- Izhod
- Stanja avtomatov
- Državni odnos
- Izhodno razmerje
Končni avtomat je sestavljen iz naslednjega:
Q : Finite set of states. ? : set of Input Symbols. q : Initial state. F : set of Final States. ? : Transition Function.>
Formalna specifikacija stroja je
{ Q, ?, q, F, ? }> FA je razdeljen na dve vrsti:
1) Deterministični končni avtomati (DFA):
arraylist razvrščena java
DFA consists of 5 tuples {Q, ?, q, F, ?}. Q : set of all states. ? : set of input symbols. ( Symbols which machine takes as input ) q : Initial state. ( Starting state of a machine ) F : set of final state. ? : Transition Function, defined as ? : Q X ? -->V.> V DFA za določen vhodni znak stroj preide samo v eno stanje. Prehodna funkcija je definirana v vsakem stanju za vsak vhodni simbol. Tudi v DFA ničelni (ali?) premik ni dovoljen, tj. DFA ne more spremeniti stanja brez vnosnega znaka.
Na primer, sestavite DFA, ki sprejme jezik vseh nizov, ki se končajo z 'a'.
Podano: ? = {a,b}, q = {q0}, F={q1}, Q = {q0, q1}
Najprej razmislite o jezikovnem nizu vseh možnih sprejemljivih nizov, da sestavite natančen diagram prehoda stanj.
L = {a, aa, aaa, aaaa, aaaaa, ba, bba, bbba, oče, oče, oče, oče}
Zgoraj je preprosta podmnožica možnih sprejemljivih nizov, lahko pa je veliko drugih nizov, ki se končajo z 'a' in vsebujejo simbole {a,b}.
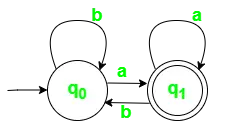
Slika 1. Diagram prehoda stanja za DFA z ? = {a, b}
Nizi niso sprejeti,
ab, bb, aab, abbb itd.
Tabela prehodov stanj za zgornji avtomat,
| ?DržavaSimbol? | a | b |
|---|---|---|
| q0 | q1 | q0 |
| q1 | q1 | q0 |
Pomembno je omeniti, za vzorec je lahko veliko možnih DFA . Na splošno je zaželen DFA z najmanjšim številom stanj.
2) Nedeterministični končni avtomati (NFA): NFA je podoben DFA, razen naslednjih dodatnih funkcij:
- Ničelen (ali?) premik je dovoljen, kar pomeni, da se lahko premika naprej brez branja simbolov.
- Sposobnost prenosa v poljubno število držav za določen vhod.
Vendar te zgornje funkcije ne dodajajo moči NFA. Če oba primerjamo po moči, sta oba enakovredna.
Zaradi zgornjih dodatnih funkcij ima NFA drugačno funkcijo prehoda, ostalo je enako kot DFA.
?: Transition Function ?: Q X (? U ? ) -->2 ^ Q.>
Kot lahko vidite v prehodni funkciji za kateri koli vnos, vključno z ničelno (ali?), lahko NFA preide v poljubno število stanj. Spodaj je na primer NFA za zgornjo težavo.
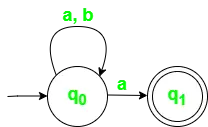
Slika 2. Diagram prehoda stanja za NFA z ? = {a, b}
Tabela prehodov stanja za zgornji avtomat,
| ?DržavaSimbol? | a | b |
|---|---|---|
| q0 | {q0,q1} | q0 |
| q1 | ? | ? |
Pomembno je omeniti, v NFA, če katera koli pot za vhodni niz vodi do končnega stanja, potem vhodni niz je sprejeto . Na primer, v zgornjem NFA obstaja več poti za vnosni niz 00. Ker ena od poti vodi do končnega stanja, zgornji NFA sprejme 00.
Nekaj pomembnih točk:
format niza java
- Obrazložitev:
In case of DFA ? : Q X ? -->Q V primeru NFA? : Q X ? --> 2Q>
Zdaj, če opazujete, boste ugotovili Q X? –> Q je del Q X? –> 2Q.
Na desni strani je Q podmnožica 2Qkar pomeni, da je Q vsebovan v 2Qali Q je del 2Qvendar pa obratno ne drži. Torej matematično lahko to sklepamo vsak DFA je NFA, ne pa obratno . Vendar pa obstaja način za pretvorbo NFA v DFA, torej za vsak NFA obstaja enakovreden DFA .
- Tako NFA kot DFA imata enako moč in vsak NFA je mogoče prevesti v DFA.
- V DFA in NFA je lahko več končnih stanj.
- NFA je bolj teoretični koncept.
- DFA se uporablja v leksikalni analizi v prevajalniku.
- Če je število stanj v NFA N, ima lahko njegov DFA največ 2nštevilo držav.
Glejte Kviz o regularnem izrazu in končnih avtomatih.
