A Usmerjeni aciklični graf , pogosto skrajšano kot DAN , je temeljni koncept v teoriji grafov. DAG-ji se uporabljajo za prikaz, kako so stvari povezane ali odvisne druga od druge na jasen in organiziran način. V tem članku bomo spoznali Usmerjeni aciklični graf , njegove lastnosti in uporaba v resničnem življenju.

Usmerjeni aciklični graf
Kaj je usmerjeni aciklični graf?
A Usmerjeni aciklični graf (DAG) je usmerjen graf, ki ne vsebuje nobenih ciklov.
Spodnji graf predstavlja usmerjeni aciklični graf (DAG):

Neposredni aciklični graf
Pomen usmerjenega acikličnega grafa:
Usmerjeni aciklični graf ima dve pomembni lastnosti:
- Usmerjeni rob s:V usmerjenem acikličnem grafu, vsak rob ima smer, kar pomeni, da gre od enega vrha (vozlišča) do drugega. Ta smer pomeni a ena smer odnos ali odvisnost med vozlišči.
- Aciklično: Izraz acikličen označuje, da v grafu ni ciklov ali zaprtih zank. Z drugimi besedami, ne morete prečkati zaporedja usmerjenih robov in se vrniti v isto vozlišče po smereh robov. Nastajanje ciklov je prepovedano v DAN. Zato je ta lastnost bistvena.

Usmerjeni aciklični graf
Lastnosti usmerjenega acikličnega grafa DAG:
Usmerjeni aciklični graf (DAG) ima različne lastnosti, zaradi katerih so uporabni pri težavah z grafi.
Obstajajo naslednje lastnosti usmerjenega acikličnega grafa (DAG):
- Razmerje dosegljivosti: V DAG lahko ugotovimo, ali obstaja razmerje dosegljivosti med dvema vozliščema. Vozlišče A naj bi bilo dosegljivo iz vozlišča B, če obstaja usmerjena pot, ki se začne v vozlišču B in konča v vozlišču A. To pomeni, da lahko sledite smeri robov v grafu, da pridete od B do A.
- Prehodno zapiranje: Tranzitivno zaprtje usmerjenega grafa je nov graf, ki predstavlja vse neposredne in posredne odnose ali povezave med vozlišči v izvirnem grafu. Z drugimi besedami, pove vam, katera vozlišča je mogoče doseči iz drugih vozlišč, če sledite enemu ali več usmerjenim robom.
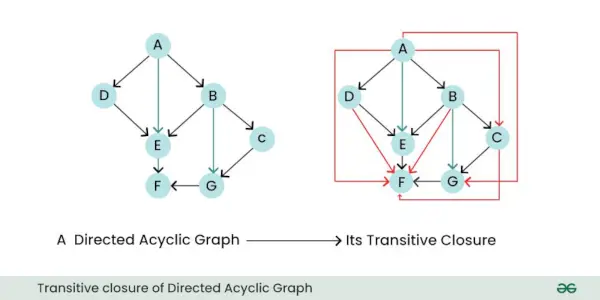
Tranzitivno zaprtje usmerjenega acikličnega grafa
- Prehodna redukcija: Prehodna redukcija usmerjenega grafa je nov graf, ki ohranja le bistvene, neposredne odnose med vozlišči, hkrati pa odstrani vse nepotrebne posredne robove. V bistvu poenostavi graf z odpravo robov, ki jih je mogoče sklepati iz preostalih robov.
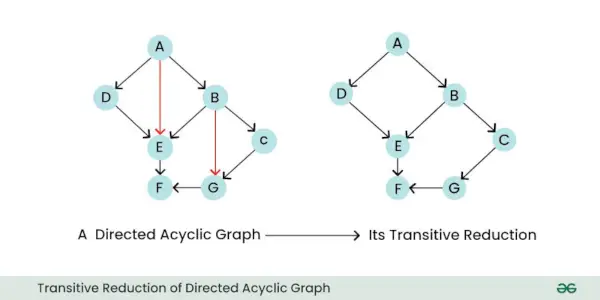
Tranzitivna redukcija usmerjenega acikličnega grafa
- Topološko urejanje: DAG je mogoče topološko razvrstiti, kar pomeni, da lahko njegova vozlišča linearno razvrstite tako, da se za vse robove začetno vozlišče roba pojavi prej v zaporedju. Ta lastnost je uporabna za naloge, kot sta razporejanje in razreševanje odvisnosti.
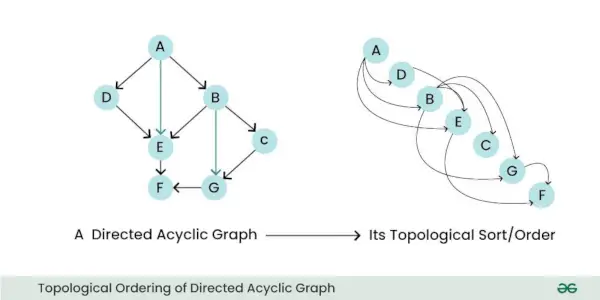
Topološko urejanje usmerjenega acikličnega grafa
Praktične uporabe DAG:
- Analiza toka podatkov: Pri oblikovanju in optimizaciji prevajalnika se DAG uporabljajo za predstavitev toka podatkov znotraj programa. To pomaga pri optimizaciji kode z identifikacijo odvečnih izračunov in mrtve kode. DAG se uporabljajo tudi za predstavitev strukture osnovni bloki v načrtovanju prevajalnika.
- Načrtovanje opravil: DAG se uporabljajo pri vodenju projektov in načrtovanju opravil. Vsaka naloga ali opravilo je predstavljeno kot vozlišče v DAG z usmerjenimi robovi, ki označujejo odvisnosti. Aciklična narava DAG zagotavlja, da so naloge načrtovane v logičnem vrstnem redu, kar preprečuje krožne odvisnosti.
Uteženi usmerjeni aciklični graf se lahko uporabi za predstavitev problema razporejanja. Vzemimo primer težave z razporejanjem opravil. Tukaj lahko vozlišče predstavlja nalogo, njegova teža pa lahko predstavlja velikost izračuna naloge. Podobno lahko rob predstavlja komunikacijo med dvema nalogama in njegova teža lahko predstavlja stroške komunikacije:
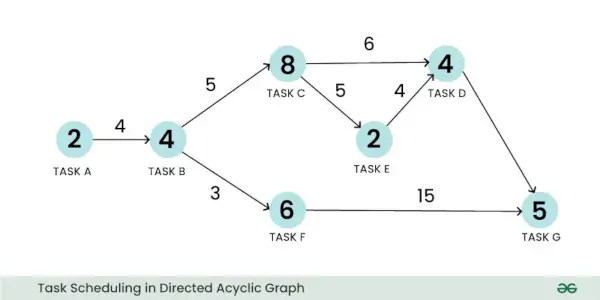
Razporejanje opravil v usmerjenem acikličnem grafu
Zaključek:
Če povzamemo, so usmerjeni aciklični grafi temeljni koncept teorije grafov s številnimi praktičnimi aplikacijami. DAG igrajo ključno vlogo pri načrtovanju nalog, analizi pretoka podatkov, reševanju odvisnosti in na različnih drugih področjih računalništva in inženiringa. Pomagajo optimizirati procese, upravljati odvisnosti in zagotoviti učinkovito izvajanje nalog ali opravil.
