Omejitve tradicionalnih binarnih iskalnih dreves so lahko frustrirajoče. Spoznajte B-Tree, večnamensko podatkovno strukturo, ki z lahkoto obravnava ogromne količine podatkov. Ko gre za shranjevanje in iskanje velikih količin podatkov, lahko tradicionalna binarna iskalna drevesa postanejo nepraktična zaradi slabe zmogljivosti in velike porabe pomnilnika. B-drevesa, znana tudi kot B-drevo ali uravnoteženo drevo, so vrsta samouravnoteženega drevesa, ki je bilo posebej zasnovano za premagovanje teh omejitev.
Za razliko od tradicionalnih binarnih iskalnih dreves je za drevesa B značilno veliko število ključev, ki jih lahko shranijo v eno vozlišče, zato so znana tudi kot drevesa velikih ključev. Vsako vozlišče v B-drevesu lahko vsebuje več ključev, kar drevesu omogoča večji faktor razvejanosti in s tem nižjo višino. Ta nizka višina povzroči manj V/I diska, kar ima za posledico hitrejše iskanje in vstavljanje. B-Trees so še posebej primerni za sisteme za shranjevanje, ki imajo počasen, obsežni dostop do podatkov, kot so trdi diski, bliskovni pomnilnik in CD-ROM-i.
B-Trees ohranja ravnotežje tako, da ima vsako vozlišče minimalno število ključev, tako da je drevo vedno uravnoteženo. To ravnovesje zagotavlja, da je časovna kompleksnost za operacije, kot so vstavljanje, brisanje in iskanje, vedno O(log n), ne glede na začetno obliko drevesa.
Časovna zapletenost B-drevesa:
| gospod št. | Algoritem | Časovna zapletenost |
|---|---|---|
| 1. | Iskanje | O(log n) |
| 2. | Vstavi | O(log n) |
| 3. | Izbriši | O(log n) |
Opomba: n je skupno število elementov v B-drevesu
gimp izvozi kot jpg
Lastnosti B-Tree:
- Vsi listi so na isti ravni.
- B-drevo je opredeljeno z izrazom najmanjša stopnja t ‘. Vrednost ' t ' je odvisno od velikosti diskovnega bloka.
- Vsako vozlišče razen korenskega mora vsebovati vsaj t-1 ključev. Korenina lahko vsebuje najmanj 1 ključ.
- Vsa vozlišča (vključno s korenom) lahko vsebujejo največ ( 2*t – 1 ) tipke.
- Število otrok vozlišča je enako številu ključev v njem plus 1 .
- Vsi ključi vozlišča so razvrščeni v naraščajočem vrstnem redu. Otrok med dvema ključema k1 in k2 vsebuje vse ključe v območju od k1 in k2 .
- B-drevo raste in se krči od korena, kar je za razliko od binarnega iskalnega drevesa. Binarna iskalna drevesa rastejo navzdol in se tudi krčijo navzdol.
- Tako kot druga uravnotežena binarna iskalna drevesa je časovna zapletenost iskanja, vstavljanja in brisanja O(log n).
- Vstavljanje vozlišča v B-drevo se zgodi samo na listnem vozlišču.
Sledi primer B-drevesa minimalnega reda 5
Opomba: da je v praktičnih B-drevesih vrednost najmanjšega naročila veliko večja od 5.

V zgornjem diagramu lahko vidimo, da so vsa listna vozlišča na isti ravni in vsi ne-listi nimajo praznega poddrevesa in imajo ključe za enega manj od števila njihovih otrok.
Zanimiva dejstva o B-drevesih:
- Najmanjša višina B-drevesa, ki lahko obstaja z n številom vozlišč in m je največje število otrok, ki jih lahko ima vozlišče, je:
- Največja višina B-drevesa, ki lahko obstaja z n številom vozlišč in t je najmanjše število otrok, ki jih lahko ima nekorensko vozlišče, je:
in
Prehod v B-drevo:
Prehod je podoben tudi prehodu po vrstnem redu binarnega drevesa. Začnemo od skrajno levega otroka, rekurzivno natisnemo skrajno levega otroka, nato ponovimo isti postopek za preostale otroke in ključe. Na koncu rekurzivno natisnite skrajno desnega otroka.
Operacija iskanja v B-Tree:
Iskanje je podobno iskanju v binarnem iskalnem drevesu. Naj bo ključ, ki ga iščemo, k.
- Začnite od korena in rekurzivno pojdite navzdol.
- Za vsako obiskano nelistno vozlišče
- Če ima vozlišče ključ, ga preprosto vrnemo.
- V nasprotnem primeru se vrnemo navzdol do ustreznega otroka (podrejenega, ki je tik pred prvim večjim ključem) vozlišča.
- Če dosežemo listno vozlišče in ne najdemo k v listnem vozlišču, potem vrne NULL.
Iskanje po drevesu B je podobno iskanju po binarnem drevesu. Algoritem je podoben in gre z rekurzijo. Na vsaki ravni je iskanje optimizirano, kot če ključna vrednost ni prisotna v obsegu nadrejenega, potem je ključ prisoten v drugi veji. Ker te vrednosti omejujejo iskanje, so znane tudi kot mejne vrednosti ali ločilne vrednosti. Če dosežemo listno vozlišče in ne najdemo želenega ključa, bo prikazano NULL.
Algoritem za iskanje elementa v B-drevesu:-
C++
struct> Node {> >int> n;> >int> key[MAX_KEYS];> >Node* child[MAX_CHILDREN];> >bool> leaf;> };> Node* BtreeSearch(Node* x,>int> k) {> >int> i = 0;> >while> (i n && k>x->tipka[i]) {> >i++;> >}> >if> (i n && k == x->tipka[i]) {> >return> x;> >}> >if> (x->list) {> >return> nullptr;> >}> >return> BtreeSearch(x->otrok[i], k);> }> |
>
>
C
BtreeSearch(x, k)> >i = 1> > >// n[x] means number of keys in x node> >while> i ? n[x] and k ? keyi[x]> >do> i = i + 1> >if> i n[x] and k = keyi[x]> >then>return> (x, i)> >if> leaf [x]> >then>return> NIL> >else> >return> BtreeSearch(ci[x], k)> |
>
>
Java
class> Node {> >int> n;> >int>[] key =>new> int>[MAX_KEYS];> >Node[] child =>new> Node[MAX_CHILDREN];> >boolean> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i =>0>;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Python3
class> Node:> >def> __init__(>self>):> >self>.n>=> 0> >self>.key>=> [>0>]>*> MAX_KEYS> >self>.child>=> [>None>]>*> MAX_CHILDREN> >self>.leaf>=> True> def> BtreeSearch(x, k):> >i>=> 0> >while> i and k>= x.key[i]: i += 1 if i and k == x.key[i]: return x if x.leaf: return None return BtreeSearch(x.child[i], k)> |
>
>
C#
class> Node {> >public> int> n;> >public> int>[] key =>new> int>[MAX_KEYS];> >public> Node[] child =>new> Node[MAX_CHILDREN];> >public> bool> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Javascript
// Define a Node class with properties n, key, child, and leaf> class Node {> >constructor() {> >this>.n = 0;> >this>.key =>new> Array(MAX_KEYS);> >this>.child =>new> Array(MAX_CHILDREN);> >this>.leaf =>false>;> >}> }> // Define a function BtreeSearch that takes in a Node object x and an integer k> function> BtreeSearch(x, k) {> >let i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Primeri:
enako java
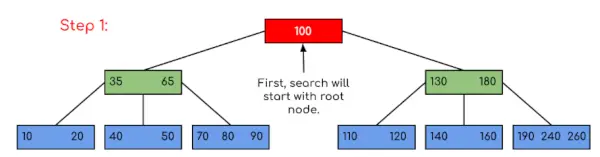
Vnos: Poiščite 120 v danem B-drevesu.
rešitev:
algoritmi za razvrščanje vstavljanja
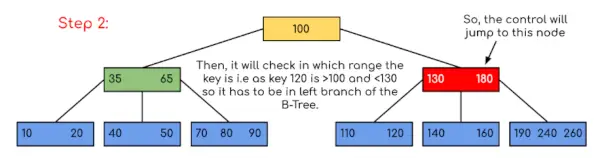
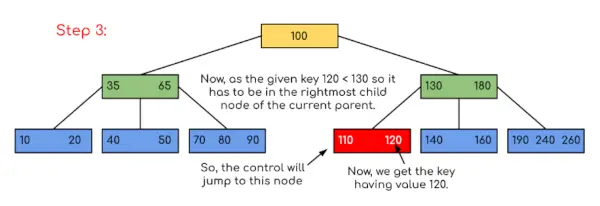
V tem primeru lahko vidimo, da je bilo naše iskanje zmanjšano samo z omejitvijo možnosti, kjer bi lahko bil prisoten ključ, ki vsebuje vrednost. Podobno, če moramo v zgornjem primeru poiskati 180, se bo nadzor ustavil pri koraku 2, ker bo program ugotovil, da je ključ 180 prisoten v trenutnem vozlišču. In podobno, če naj išče 90, potem kot 90 <100, tako da bo samodejno šel v levo poddrevo, zato bo kontrolni tok potekal podobno, kot je prikazano v zgornjem primeru.
Spodaj je izvedba zgornjega pristopa:
C++
// C++ implementation of search() and traverse() methods> #include> using> namespace> std;> // A BTree node> class> BTreeNode {> >int>* keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode** C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> public>:> >BTreeNode(>int> _t,>bool> _leaf);>// Constructor> >// A function to traverse all nodes in a subtree rooted> >// with this node> >void> traverse();> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode*> >search(>int> k);>// returns NULL if k is not present.> >// Make the BTree friend of this so that we can access> >// private members of this class in BTree functions> >friend> class> BTree;> };> // A BTree> class> BTree {> >BTreeNode* root;>// Pointer to root node> >int> t;>// Minimum degree> public>:> >// Constructor (Initializes tree as empty)> >BTree(>int> _t)> >{> >root = NULL;> >t = _t;> >}> >// function to traverse the tree> >void> traverse()> >{> >if> (root != NULL)> >root->premik();> >}> >// function to search a key in this tree> >BTreeNode* search(>int> k)> >{> >return> (root == NULL) ? NULL : root->iskanje(k);> >}> };> // Constructor for BTreeNode class> BTreeNode::BTreeNode(>int> _t,>bool> _leaf)> {> >// Copy the given minimum degree and leaf property> >t = _t;> >leaf = _leaf;> >// Allocate memory for maximum number of possible keys> >// and child pointers> >keys =>new> int>[2 * t - 1];> >C =>new> BTreeNode*[2 * t];> >// Initialize the number of keys as 0> >n = 0;> }> // Function to traverse all nodes in a subtree rooted with> // this node> void> BTreeNode::traverse()> {> >// There are n keys and n+1 children, traverse through n> >// keys and first n children> >int> i;> >for> (i = 0; i // If this is not leaf, then before printing key[i], // traverse the subtree rooted with child C[i]. if (leaf == false) C[i]->prečni(); cout<< ' ' << keys[i]; } // Print the subtree rooted with last child if (leaf == false) C[i]->prečni(); } // Funkcija za iskanje ključa k v poddrevesu, ukoreninjenem s tem vozliščem BTreeNode* BTreeNode::search(int k) { // Poišči prvi ključ, ki je večji ali enak k int i = 0; medtem ko (i tipke[i]) i++; // Če je najdeni ključ enak k, vrni to vozlišče if (keys[i] == k) vrni to; // Če ključ ni najden tukaj in je to listno vozlišče if (leaf == true) return NULL; // Pojdi do ustreznega podrejenega vrnitve C[i]->search(k); }> |
>
>
Java
// Java program to illustrate the sum of two numbers> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >System.out.println();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >boolean> >leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>boolean> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[>2> * t ->1>];> >this>.C =>new> BTreeNode[>2> * t];> >this>.n =>0>;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i =>0>;> >for> (i =>0>; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >System.out.print(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i =>0>;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> |
>
>
Python3
# Create a node> class> BTreeNode:> >def> __init__(>self>, leaf>=>False>):> >self>.leaf>=> leaf> >self>.keys>=> []> >self>.child>=> []> # Tree> class> BTree:> >def> __init__(>self>, t):> >self>.root>=> BTreeNode(>True>)> >self>.t>=> t> ># Insert node> >def> insert(>self>, k):> >root>=> self>.root> >if> len>(root.keys)>=>=> (>2> *> self>.t)>-> 1>:> >temp>=> BTreeNode()> >self>.root>=> temp> >temp.child.insert(>0>, root)> >self>.split_child(temp,>0>)> >self>.insert_non_full(temp, k)> >else>:> >self>.insert_non_full(root, k)> ># Insert nonfull> >def> insert_non_full(>self>, x, k):> >i>=> len>(x.keys)>-> 1> >if> x.leaf:> >x.keys.append((>None>,>None>))> >while> i>>=> 0> and> k[>0>] 0]: x.keys[i + 1] = x.keys[i] i -= 1 x.keys[i + 1] = k else: while i>= 0 in k[0] 0]: i -= 1 i += 1 if len(x.child[i].keys) == (2 * self.t) - 1: self.split_child(x, i) if k[0]> x.keys[i][0]: i += 1 self.insert_non_full(x.child[i], k) # Razdeli otroka def split_child(self, x, i): t = self .t y = x.child[i] z = BTreeNode(y.leaf) x.child.insert(i + 1, z) x.keys.insert(i, y.keys[t - 1]) z.keys = y.keys[t: (2 * t) - 1] y.keys = y.keys[0: t - 1] če ne y.leaf: z.child = y.child[t: 2 * t] y. otrok = y.child[0: t - 1] # Natisni drevo def print_tree(self, x, l=0): print('Raven ', l, ' ', len(x.keys), end=':') za i v x.keys: print(i, end=' ') print() l += 1 če je len(x.child)> 0: za i v x.child: self.print_tree(i, l) # Iskalni ključ v drevesu def search_key(self, k, x=None): če x ni None: i = 0 medtem ko i |
>
>
C#
// C# program to illustrate the sum of two numbers> using> System;> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >Console.WriteLine();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>bool> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[2 * t - 1];> >this>.C =>new> BTreeNode[2 * t];> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i = 0;> >for> (i = 0; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >Console.Write(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >public> BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i = 0;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by Rajput-Ji> |
>
>
Javascript
// Javascript program to illustrate the sum of two numbers> // A BTree> class Btree> {> >// Constructor (Initializes tree as empty)> >constructor(t)> >{> >this>.root =>null>;> >this>.t = t;> >}> > >// function to traverse the tree> >traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >document.write(>' '>);> >}> > >// function to search a key in this tree> >search(k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> > }> // A BTree node> class BTreeNode> {> >// Constructor> >constructor(t,leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> Array(2 * t - 1);> >this>.C =>new> Array(2 * t);> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted with this node> >traverse()> >{> >// There are n keys and n+1 children, traverse through n keys> >// and first n children> >let i = 0;> >for> (i = 0; i <>this>.n; i++) {> > >// If this is not leaf, then before printing key[i],> >// traverse the subtree rooted with child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >document.write(keys[i] +>' '>);> >}> > >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> > >// A function to search a key in the subtree rooted with this node.> >search(k)>// returns NULL if k is not present.> >{> > >// Find the first key greater than or equal to k> >let i = 0;> >while> (i keys[i])> >i++;> > >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> > >// If the key is not found here and this is a leaf node> >if> (leaf ==>true>)> >return> null>;> > >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by patel2127> |
>
>
Opomba: Zgornja koda ne vsebuje programa gonilnika. Celoten program bomo obravnavali v naši naslednji objavi Vstavljanje B-drevesa .
Obstajata dve konvenciji za definiranje B-drevesa, ena je opredelitev z minimalno stopnjo, druga je opredelitev z vrstnim redom. Upoštevali smo konvencijo o minimalni diplomi in jo bomo upoštevali v prihodnjih objavah na B-Tree. Tudi imena spremenljivk, uporabljena v zgornjem programu, ostanejo enaka
obratni niz v Javi
Uporaba B-Trees:
- Uporablja se v velikih zbirkah podatkov za dostop do podatkov, shranjenih na disku
- Iskanje podatkov v nizu podatkov je mogoče doseči v bistveno krajšem času z uporabo B-Tree
- S funkcijo indeksiranja je mogoče doseči večnivojsko indeksiranje.
- Večina strežnikov uporablja tudi pristop B-drevesa.
- B-drevesa se uporabljajo v sistemih CAD za organiziranje in iskanje geometrijskih podatkov.
- B-drevesa se uporabljajo tudi na drugih področjih, kot so obdelava naravnega jezika, računalniška omrežja in kriptografija.
Prednosti B-Trees:
- B-drevesa imajo zajamčeno časovno kompleksnost O(log n) za osnovne operacije, kot so vstavljanje, brisanje in iskanje, zaradi česar so primerna za velike nabore podatkov in aplikacije v realnem času.
- B-drevesa so samouravnotežena.
- Visoka sočasnost in visoka prepustnost.
- Učinkovita uporaba prostora za shranjevanje.
Slabosti B-Trees:
- B-Drevesa temeljijo na podatkovnih strukturah na disku in imajo lahko visoko porabo diska.
- Ni najboljše za vse primere.
- Počasen v primerjavi z drugimi podatkovnimi strukturami.
Vstavljanje in brisanje:
Vstavljanje B-drevesa
Izbris B-drevesa