Algoritemski svet je čudovit z različnimi strategijami in orodji, ki se nenehno razvijajo, da bi zadovoljili potrebe po visoko zmogljivem računalništvu. Pravzaprav, ko se algoritmi zgledujejo po naravnih zakonih, opazimo zanimive rezultate. V tak razred algoritmov spadajo evolucijski algoritmi. Ti algoritmi so zasnovani tako, da posnemajo določeno vedenje in tudi evolucijske lastnosti človeškega genoma. Poleg tega taka algoritemska zasnova ni omejena le na ljudi, ampak se lahko zgleduje tudi po naravnem vedenju nekaterih živali. Osnovni cilj izdelave takšnih metodologij je zagotoviti realistične, ustrezne in hkrati poceni rešitve za probleme, ki so bili doslej nerešljivi s konvencionalnimi sredstvi.
Na podlagi takšnih evolucijskih algoritmov so se tako razvile različne optimizacijske tehnike in s tem odprle področje metahevristike. Metaevristično je izpeljana iz dveh grških besed, in sicer Meta pomen eno raven višje in heuriskein pomen najti . Algoritmi, kot sta optimizacija roja delcev (PSO) in optimizacija kolonije mravelj (ACO), sta primera inteligence roja in metahevristike. Cilj inteligence rojev je oblikovati inteligentne sisteme z več agenti po navdihu pri kolektivnem vedenju družbenih žuželk, kot so mravlje, termiti, čebele, ose in drugih živalskih družb, kot so jate ptic ali jate rib.
Ozadje:
Tehnika optimizacije kolonije mravljincev se je povsem zgledovala po iskanje hrane obnašanje kolonij mravelj, ki ga je prvi predstavil Marco Dorigo v devetdesetih letih prejšnjega stoletja. Mravlje so evsocialne žuželke, ki raje preživijo in vzdržujejo skupnost kot kot posamezne vrste. Med seboj se sporazumevajo z zvokom, dotikom in feromonom. Feromoni so organske kemične spojine, ki jih izločajo mravlje in sprožijo družbeni odziv pri pripadnikih iste vrste. To so kemikalije, ki lahko zunaj telesa posameznika, ki izloča, delujejo kot hormoni in vplivajo na vedenje posameznikov, ki jih prejemajo. Ker večina mravelj živi na tleh, uporabljajo površino zemlje, da pustijo feromonske sledi, ki jim lahko sledijo (zavohajo) druge mravlje.
Mravlje živijo v skupnih gnezdih in osnovno načelo ACO je opazovanje gibanja mravelj iz njihovih gnezd, da bi poiskali hrano po najkrajši možni poti. Sprva se mravlje začnejo naključno premikati v iskanju hrane okoli svojih gnezd. To naključno iskanje odpre več poti od gnezda do vira hrane. Zdaj, glede na kakovost in količino hrane, mravlje na svoji povratni poti odnesejo del hrane nazaj s potrebno koncentracijo feromonov. Glede na te poskuse s feromoni bi bila verjetnost, da bodo naslednje mravlje izbrale določeno pot, vodilni dejavnik pri viru hrane. Očitno ta verjetnost temelji na koncentraciji in hitrosti izhlapevanja feromona. Opaziti je mogoče tudi, da je dolžino vsake poti enostavno upoštevati, ker je tudi hitrost izhlapevanja feromona odločilni dejavnik.
char in int java
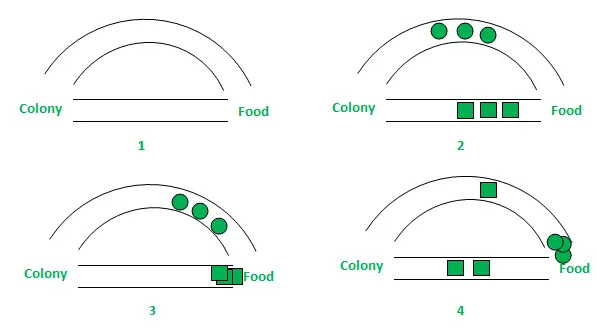
Na zgornji sliki sta zaradi poenostavitve upoštevani le dve možni poti med virom hrane in gnezdom mravelj. Faze je mogoče analizirati na naslednji način:
- 1. stopnja: Vse mravlje so v svojem gnezdu. V okolju ni vsebnosti feromonov. (Za algoritemsko zasnovo se lahko upošteva preostala količina feromona, ne da bi posegali v verjetnost.) Faza 2: Mravlje začnejo iskanje z enako verjetnostjo (0,5 vsaka) na vsaki poti. Jasno je, da je ukrivljena pot daljša, zato je čas, ki ga mravlje potrebujejo, da dosežejo vir hrane, daljši od drugega. Faza 3: Mravlje po krajši poti prej dosežejo vir hrane. Zdaj se očitno soočajo s podobno izbirno dilemo, vendar je tokrat zaradi feromonske sledi po krajši poti, ki je že na voljo, verjetnost izbire večja. Faza 4: Več mravelj se vrne po krajši poti in posledično se povečajo tudi koncentracije feromonov. Poleg tega se zaradi izhlapevanja koncentracija feromona na daljši poti zmanjša, kar zmanjša verjetnost izbire te poti v nadaljnjih stopnjah. Zato celotna kolonija postopoma uporablja krajšo pot pri večjih verjetnostih. Torej je dosežena optimizacija poti.
Algoritemska zasnova:
V zvezi z zgornjim vedenjem mravelj je zdaj mogoče razviti algoritemsko zasnovo. Zaradi poenostavitve sta bili obravnavani en sam vir hrane in ena sama kolonija mravelj s samo dvema možnima potoma prečkanja. Celoten scenarij je mogoče realizirati s pomočjo tehtanih grafov, kjer kolonija mravelj in vir hrane delujeta kot vozlišča (ali vozlišča); poti služijo kot robovi, vrednosti feromonov pa so uteži, povezane z robovi.
Naj bo graf G = (V, E) kjer sta V, E robovi in oglišča grafa. Oglišča po našem upoštevanju so INs (Izvorno vertex – kolonija mravelj) in INd (Ciljno oglišče – vir hrane), dva robova sta IN1 in IN2 z dolžinami L1 in L2 dodeljen vsakemu. Zdaj se lahko domneva, da so povezane vrednosti feromonov (ki kažejo njihovo moč). R1 in R2 za vozlišča E1in E2oz. Tako je za vsako mravljo začetna verjetnost izbire poti (med E1in E2) se lahko izrazi kot sledi:
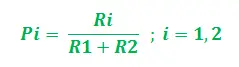
Očitno, če R1>R2, verjetnost izbire E1je višja in obratno. Zdaj, ko se vračate po tej najkrajši poti, recite Ejaz, se vrednost feromona posodobi za ustrezno pot. Posodobitev se izvede na podlagi dolžine poti in stopnje izhlapevanja feromona. Posodobitev je torej mogoče postopoma izvesti na naslednji način:
- Glede na dolžino poti –
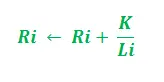
V zgornji posodobitvi i = 1, 2 in 'K' služi kot parameter modela. Poleg tega je posodobitev odvisna od dolžine poti. Krajša je pot, višji je dodan feromon. Glede na hitrost izhlapevanja feromona –
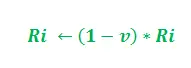
Parameter 'v' pripada intervalu (0, 1], ki uravnava izhlapevanje feromona. Nadalje, i = 1, 2.
Pri vsaki ponovitvi so vse mravlje postavljene na izvorno točko Vs(kolonija mravelj). Nato se mravlje premaknejo iz Vsdo Vd(vir hrane) po 1. koraku. Nato vse mravlje opravijo povratno potovanje in okrepijo svojo izbrano pot na podlagi 2. koraka.
Psevdokoda:
življenjski cikel sdlc
Procedure AntColonyOptimization: Initialize necessary parameters and pheromone trials; while not termination do : Generate ant population; Calculate fitness values associated with each ant; Find best solution through selection methods; Update pheromone trial; end while end procedure>
Posodobitev feromonov in izračune primernosti v zgornji psevdokodi je mogoče najti prek zgoraj omenjenih postopnih izvedb.
Tako je uveljavljena uvedba optimizacijske tehnike ACO. Uporaba ACO se lahko razširi na različne težave, kot je slavni TSP (Travelling Salesman Problem) .
Reference:
https://www.ics.uci.edu/~welling/teaching/271fall09/antcolonyopt.pdf
