- Algoritem za plezanje po hribu je algoritem lokalnega iskanja, ki se nenehno premika v smeri naraščajoče nadmorske višine/vrednosti, da najde vrh gore ali najboljšo rešitev problema. Konča se, ko doseže najvišjo vrednost, kjer noben sosed nima višje vrednosti.
- Algoritem plezanja po hribu je tehnika, ki se uporablja za optimizacijo matematičnih problemov. Eden izmed široko razpravljanih primerov algoritma za plezanje po hribu je problem trgovskega potnika, pri katerem moramo zmanjšati razdaljo, ki jo prevozi prodajalec.
- Imenuje se tudi pohlepno lokalno iskanje, saj gleda samo na svojo dobro neposredno sosednjo državo in ne dlje.
- Vozlišče algoritma za vzpenjanje ima dve komponenti, in sicer stanje in vrednost.
- Plezanje v hrib se večinoma uporablja, ko je na voljo dobra hevristika.
- V tem algoritmu nam ni treba vzdrževati in obravnavati iskalnega drevesa ali grafa, saj hrani samo eno trenutno stanje.
Lastnosti plezanja po hribu:
Sledi nekaj glavnih značilnosti algoritma za plezanje v hribe:
Diagram prostora stanja za plezanje v hribe:
Pokrajina prostora stanja je grafična predstavitev algoritma za plezanje po hribu, ki prikazuje graf med različnimi stanji algoritma in ciljno funkcijo/ceno.
Na os Y smo vzeli funkcijo, ki je lahko ciljna funkcija ali stroškovna funkcija, in prostor stanja na os x. Če je funkcija na osi Y cena, potem je cilj iskanja najti globalni minimum in lokalni minimum. Če je funkcija osi Y ciljna funkcija, je cilj iskanja najti globalni maksimum in lokalni maksimum.
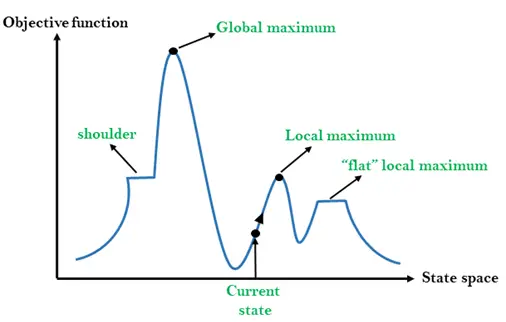
Različne regije v pokrajini državnega prostora:
Lokalni maksimum: Lokalni maksimum je stanje, ki je boljše od sosednjih stanj, obstaja pa tudi drugo stanje, ki je višje od njega.
Globalni maksimum: Globalni maksimum je najboljše možno stanje krajine državnega prostora. Ima najvišjo vrednost objektivne funkcije.
Trenutno stanje: To je stanje v pokrajinskem diagramu, kjer je agent trenutno prisoten.
Ravni lokalni maksimum: To je raven prostor v pokrajini, kjer imajo vse sosednje države sedanjih držav enako vrednost.
Rama: To je planota, ki ima vzpetino.
Vrste algoritmov za plezanje v hribe:
- Preprosto plezanje v hrib:
- Najstrmejši vzpon v hrib:
- Stohastično plezanje v hrib:
1. Preprosto plezanje v hrib:
Preprosto plezanje v hrib je najpreprostejši način za implementacijo algoritma za plezanje v hrib. Naenkrat oceni le stanje sosednjega vozlišča in izbere prvo, ki optimizira trenutne stroške, ter ga nastavi kot trenutno stanje . Preveri le, ali gre za eno nasledstveno stanje, in če ugotovi, da je boljše od trenutnega stanja, se premakni, da ostane v istem stanju. Ta algoritem ima naslednje lastnosti:
- Manj časa
- Manj optimalna rešitev in rešitev ni zagotovljena
Algoritem za preprosto plezanje v hrib:
- Če je ciljno stanje, vrnite uspeh in zapustite.
- V nasprotnem primeru, če je boljše od trenutnega stanja, dodelite novo stanje kot trenutno stanje.
- Če ni boljše od trenutnega stanja, se vrnite na 2. korak.
2. Plezanje v hrib z najstrmejšim vzponom:
Algoritem najstrmejšega vzpona je različica preprostega algoritma za plezanje po hribu. Ta algoritem pregleda vsa sosednja vozlišča trenutnega stanja in izbere eno sosednje vozlišče, ki je najbližje ciljnemu stanju. Ta algoritem porabi več časa, saj išče več sosedov
Algoritem za vzpon z najstrmejšim vzponom:
- Naj bo SUCC takšna država, da bo vsaka naslednica sedanje države boljša od nje.
- Za vsak operator, ki velja za trenutno stanje:
- Uporabite nov operater in ustvarite novo stanje.
- Ocenite novo stanje.
- Če je ciljno stanje, ga vrnite in zaprite, sicer ga primerjajte s SUCC.
- Če je boljši od SUCC, nastavite novo stanje kot SUCC.
- Če je SUCC boljši od trenutnega stanja, nastavite trenutno stanje na SUCC.
3. Stohastično plezanje v hribe:
Stohastično plezanje po hribu ne pregleda vseh svojih sosedov, preden se premakne. Namesto tega iskalni algoritem naključno izbere eno sosednje vozlišče in se odloči, ali ga bo izbral kot trenutno stanje ali pregledal drugo stanje.
Težave v algoritmu za plezanje v hrib:
1. Lokalni maksimum: Lokalni maksimum je najvišje stanje v pokrajini, ki je boljše od vsakega od sosednjih stanj, vendar je prisotno tudi drugo stanje, ki je višje od lokalnega maksimuma.
rešitev: Tehnika povratnega sledenja je lahko rešitev lokalnega maksimuma v pokrajini prostora stanja. Ustvarite seznam obetavnih poti, tako da lahko algoritem vrne iskalni prostor in razišče tudi druge poti.

2. Planota: Plato je ravno območje iskalnega prostora, v katerem vsa sosednja stanja trenutnega stanja vsebujejo enako vrednost, ker ta algoritem ne najde nobene najboljše smeri za premikanje. Iskanje po hribu se lahko izgubi na območju planote.
rešitev: Rešitev za plato je, da med iskanjem naredite velike ali zelo majhne korake, da rešite problem. Naključno izberite stanje, ki je daleč od trenutnega stanja, tako da je možno, da bi algoritem našel območje brez platoja.

3. Grebeni: Greben je posebna oblika lokalnega maksimuma. Ima območje, ki je višje od okoliških območij, vendar ima samo pobočje in ga ni mogoče doseči z eno potezo.
Igralka Sai Pallavi
rešitev: Z uporabo dvosmernega iskanja ali premikanjem v različnih smereh lahko to težavo izboljšamo.

Simulirano žarjenje:
Algoritem za vzpenjanje, ki se nikoli ne premakne proti nižji vrednosti, je zagotovljeno nepopoln, ker se lahko zatakne na lokalnem maksimumu. In če algoritem uporabi naključni sprehod s premikanjem naslednika, se lahko dokonča, vendar ne bo učinkovit. Simulirano žarjenje je algoritem, ki zagotavlja učinkovitost in popolnost.
V mehanskem smislu Žarjenje je postopek utrjevanja kovine ali stekla na visoko temperaturo, ki se nato postopoma ohlaja, tako da kovina doseže nizkoenergijsko kristalno stanje. Isti postopek se uporablja pri simuliranem žarjenju, pri katerem algoritem izbere naključno potezo, namesto da izbere najboljšo potezo. Če naključna poteza izboljša stanje, potem sledi isti poti. V nasprotnem primeru algoritem sledi poti, ki ima verjetnost manjšo od 1 ali pa se pomakne navzdol in izbere drugo pot.
