Ford-Fulkersonov algoritem je pogosto uporabljen algoritem za reševanje problema največjega pretoka v pretočnem omrežju. Problem z največjim pretokom vključuje določanje največje količine pretoka, ki se lahko pošlje od izvorne točke do ponorne točke v usmerjenem uteženem grafu, ob upoštevanju omejitev zmogljivosti na robovih.
Algoritem deluje tako, da iterativno najde povečevalno pot, ki je pot od vira do ponora v preostalem grafu, tj. grafu, dobljenem z odštevanjem trenutnega toka od zmogljivosti vsakega roba. Algoritem nato poveča pretok vzdolž te poti za največjo možno količino, ki je najmanjša zmogljivost robov vzdolž poti.
Težava:
Podan je graf, ki predstavlja tokovno mrežo, kjer ima vsak rob kapaciteto. Tudi glede na dve točki vir 's' in umivalnik 't' na grafu poiščite največji možni pretok od s do t z naslednjimi omejitvami:
- Pretok na robu ne presega dane zmogljivosti roba.
- Vhodni tok je enak odhodnemu toku za vsako točko razen s in t.
Na primer, razmislite o naslednjem grafu iz knjige CLRS.
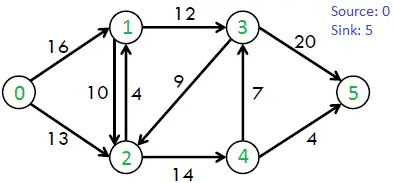
Največji možni pretok v zgornjem grafu je 23.

Predpogoj: Uvod v problem največjega pretoka
Ford-Fulkersonov algoritem
kako pretvoriti celo število v niz v JaviSledi preprosta ideja Ford-Fulkersonovega algoritma:
- Začnite z začetnim pretokom kot 0.
- Čeprav obstaja dopolnilna pot od vira do ponora:
- Poiščite dopolnilno pot s katerim koli algoritmom za iskanje poti, kot je iskanje v širino ali iskanje v globino.
- Določite količino pretoka, ki se lahko pošlje vzdolž povečevalne poti, kar je najmanjša preostala zmogljivost vzdolž robov poti.
- Povečajte pretok vzdolž povečevalne poti za določeno količino.
- Vrnite največji pretok.
Časovna zapletenost: Časovna kompleksnost zgornjega algoritma je O(max_flow * E). Izvajamo zanko, medtem ko obstaja dopolnilna pot. V najslabšem primeru lahko dodamo 1 pretok enote v vsaki ponovitvi. Zato postane časovna kompleksnost O(max_flow * E).
Kako implementirati zgornji preprost algoritem?
Najprej opredelimo koncept Residual Graph, ki je potreben za razumevanje izvedbe.
Graf ostankov pretočne mreže je graf, ki prikazuje dodatne možne pretoke. Če obstaja pot od izvora do ponora v rezidualnem grafu, potem je mogoče dodati tok. Vsak rob preostalega grafa ima vrednost, imenovano preostala zmogljivost ki je enak prvotni zmogljivosti roba minus tokovni tok. Preostala zmogljivost je v bistvu trenutna zmogljivost roba.
Pogovorimo se zdaj o podrobnostih izvajanja. Preostala zmogljivost je 0, če med dvema točkama preostalega grafa ni roba. Graf ostankov lahko inicializiramo kot izvirni graf, saj ni začetnega pretoka in je začetna preostala zmogljivost enaka prvotni zmogljivosti. Če želite najti pot povečanja, lahko naredimo BFS ali DFS rezidualnega grafa. V spodnji izvedbi smo uporabili BFS. S pomočjo BFS lahko ugotovimo, ali obstaja pot od izvira do ponora. BFS prav tako gradi parent[] array. Z uporabo matrike parent[] prečkamo najdeno pot in poiščemo možen pretok skozi to pot tako, da poiščemo minimalno preostalo zmogljivost na poti. Pozneje najdeni tok poti dodamo skupnemu toku.
Pomembno je, da moramo posodobiti preostale zmogljivosti v grafu preostalih. Tok poti odštejemo od vseh robov vzdolž poti in dodamo tok poti vzdolž vzvratnih robov. Dodati moramo tok poti vzdolž vzvratnih robov, ker bo morda kasneje treba poslati tok v obratni smeri (za primer glejte naslednjo povezavo).
Spodaj je implementacija Ford-Fulkersonovega algoritma. Za poenostavitev je graf predstavljen kot 2D matrika.
C++
// C++ program for implementation of Ford Fulkerson> // algorithm> #include> #include> #include> #include> using> namespace> std;> // Number of vertices in given graph> #define V 6> /* Returns true if there is a path from source 's' to sink> >'t' in residual graph. Also fills parent[] to store the> >path */> bool> bfs(>int> rGraph[V][V],>int> s,>int> t,>int> parent[])> {> >// Create a visited array and mark all vertices as not> >// visited> >bool> visited[V];> >memset>(visited, 0,>sizeof>(visited));> >// Create a queue, enqueue source vertex and mark source> >// vertex as visited> >queue<>int>>q;> >q.push(s);> >visited[s] =>true>;> >parent[s] = -1;> >// Standard BFS Loop> >while> (!q.empty()) {> >int> u = q.front();> >q.pop();> >for> (>int> v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Če najdemo povezavo s ponornim vozliščem, // potem BFS nima več smisla. // Samo nastaviti moramo njegov nadrejeni in lahko vrnemo // true if (v == t) { nadrejeni [ v] = u; vrni resnico; } q.push(v); nadrejeni [v] = u; obiskano [v] = res; } } } // Nismo dosegli ponora v BFS, začenši od vira, zato // vrni false return false; } // Vrne največji pretok od s do t v danem grafu int fordFulkerson(int graph[V][V], int s, int t) { int u, v; // Ustvari rezidualni graf in zapolni rezidualni graf // z danimi zmogljivostmi v izvirnem grafu kot // preostale kapacitete v rezidualnem grafu int rGraph[V] [V]; // Graf ostankov, kjer rGraph[i][j] // označuje preostalo zmogljivost roba // od i do j (če rob obstaja. Če je // rGraph[i][j] 0, potem ga ni) for (u = 0; u for (v = 0; v rGraph[u][v] = graph[u][v]; int parent[V]; // To matriko polni BFS in // shrani pot int max_flow = 0; // Na začetku ni toka // Povečaj tok, medtem ko obstaja pot od vira do // ponora while (bfs(rGraph, s, t, parent)) { // Poišči minimalno preostalo zmogljivost robov // pot, ki jo je zapolnil BFS. Ali lahko rečemo, da najdemo največji tok skozi najdeno pot int_flow = INT_MAX; for (v = t; v != s; v = parent[v]) { u = parent[v]; path_flow = min(path_flow, rGraph[u][v]); // posodobitev preostalih zmogljivosti robov in // obratnih robov vzdolž poti za (v = t; v != s; v = parent[v]) {u = parent[v]; rGraph[u][v] -= path_flow; rGraph[v][u] += path_flow } // Dodaj tok poti max_flow // Vrni skupni tok return max_flow; } // Program gonilnika za testiranje zgoraj navedenih funkcij int main() { // Ustvarimo graf, prikazan v zgornjem primeru int graph[V][V] = { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7 , 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; cout<< 'The maximum possible flow is ' << fordFulkerson(graph, 0, 5); return 0; }> |
>
>
Java
// Java program for implementation of Ford Fulkerson> // algorithm> import> java.io.*;> import> java.lang.*;> import> java.util.*;> import> java.util.LinkedList;> class> MaxFlow {> >static> final> int> V =>6>;>// Number of vertices in graph> >/* Returns true if there is a path from source 's' to> >sink 't' in residual graph. Also fills parent[] to> >store the path */> >boolean> bfs(>int> rGraph[][],>int> s,>int> t,>int> parent[])> >{> >// Create a visited array and mark all vertices as> >// not visited> >boolean> visited[] =>new> boolean>[V];> >for> (>int> i =>0>; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited LinkedList queue = new LinkedList(); queue.add(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.size() != 0) { int u = queue.poll(); for (int v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Če najdemo povezavo s ponornim // vozliščem, potem v BFS // ni več smisla. Samo nastaviti moramo njegov nadrejeni // in lahko vrnemo true if (v == t) { nadrejeni [ v] = u; vrni resnico; } queue.add(v); nadrejeni [v] = u; obiskano [v] = res; } } } // Nismo dosegli ponora v BFS, začenši od izvora, // zato vrni false return false; } // Vrne največji pretok od s do t v danem // grafu int fordFulkerson(int graph[][], int s, int t) { int u, v; // Ustvari rezidualni graf in izpolni rezidualni // graf z danimi zmogljivostmi v izvirnem grafu // kot preostale kapacitete v rezidualnem grafu // Rezidualni graf, kjer rGraph[i][j] označuje // preostalo kapaciteto roba od i do j (če // obstaja rob. Če je rGraph[i][j] 0, potem ga // ni) int rGraph[][] = novo int[V][V]; for (u = 0; u for (v = 0; v rGraph[u][v] = graph[u][v]; // To matriko polni BFS in za shranjevanje poti int parent[] = new int[ V]; int max_flow = 0; // Na začetku ni toka // Povečajte tok, medtem ko obstaja pot od izvora // do ponora (bfs(rGraph, s, t, parent)) { // Poiščite najmanjšo preostalo zmogljivost robov // vzdolž poti, ki jo je zapolnil BFS. Ali pa lahko rečemo, da najdemo največji tok skozi najdeno pot int path_flow = Integer.MAX_VALUE; za (v = t; v != s; v = parent[v ]) { u = parent[v]; path_flow = Math.min(path_flow, rGraph[u][v]); // posodobimo preostale zmogljivosti robov in // obrnemo robove vzdolž poti (v = t; v != s; v = parent[v]; rGraph[u][v] -= path_flow; rGraph[v][u] += path_flow; } // Dodajanje poti toka flow max_flow += path_flow; } // Vrne skupni tok return max_flow } // Program gonilnika za testiranje zgornjih funkcij public static void main(String[] args) throws java.lang.Exception { // Ustvarimo prikazani graf v zgornjem primeru int graph[][] = new int[][] { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4 , 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7, 0, 4}, { 0, 0, 0, 0, 0, 0 } }; MaxFlow m = nov MaxFlow(); System.out.println('Največji možni pretok je ' + m.fordFulkerson(graf, 0, 5)); } }> |
>
skeniranje java
>
Python
# Python program for implementation> # of Ford Fulkerson algorithm> from> collections>import> defaultdict> # This class represents a directed graph> # using adjacency matrix representation> class> Graph:> >def> __init__(>self>, graph):> >self>.graph>=> graph># residual graph> >self>. ROW>=> len>(graph)> ># self.COL = len(gr[0])> >'''Returns true if there is a path from source 's' to sink 't' in> >residual graph. Also fills parent[] to store the path '''> >def> BFS(>self>, s, t, parent):> ># Mark all the vertices as not visited> >visited>=> [>False>]>*>(>self>.ROW)> ># Create a queue for BFS> >queue>=> []> ># Mark the source node as visited and enqueue it> >queue.append(s)> >visited[s]>=> True> ># Standard BFS Loop> >while> queue:> ># Dequeue a vertex from queue and print it> >u>=> queue.pop(>0>)> ># Get all adjacent vertices of the dequeued vertex u> ># If a adjacent has not been visited, then mark it> ># visited and enqueue it> >for> ind, val>in> enumerate>(>self>.graph[u]):> >if> visited[ind]>=>=> False> and> val>>0>:> ># If we find a connection to the sink node,> ># then there is no point in BFS anymore> ># We just have to set its parent and can return true> >queue.append(ind)> >visited[ind]>=> True> >parent[ind]>=> u> >if> ind>=>=> t:> >return> True> ># We didn't reach sink in BFS starting> ># from source, so return false> >return> False> > > ># Returns the maximum flow from s to t in the given graph> >def> FordFulkerson(>self>, source, sink):> ># This array is filled by BFS and to store path> >parent>=> [>->1>]>*>(>self>.ROW)> >max_flow>=> 0> # There is no flow initially> ># Augment the flow while there is path from source to sink> >while> self>.BFS(source, sink, parent) :> ># Find minimum residual capacity of the edges along the> ># path filled by BFS. Or we can say find the maximum flow> ># through the path found.> >path_flow>=> float>(>'Inf'>)> >s>=> sink> >while>(s !>=> source):> >path_flow>=> min> (path_flow,>self>.graph[parent[s]][s])> >s>=> parent[s]> ># Add path flow to overall flow> >max_flow>+>=> path_flow> ># update residual capacities of the edges and reverse edges> ># along the path> >v>=> sink> >while>(v !>=> source):> >u>=> parent[v]> >self>.graph[u][v]>->=> path_flow> >self>.graph[v][u]>+>=> path_flow> >v>=> parent[v]> >return> max_flow> > # Create a graph given in the above diagram> graph>=> [[>0>,>16>,>13>,>0>,>0>,>0>],> >[>0>,>0>,>10>,>12>,>0>,>0>],> >[>0>,>4>,>0>,>0>,>14>,>0>],> >[>0>,>0>,>9>,>0>,>0>,>20>],> >[>0>,>0>,>0>,>7>,>0>,>4>],> >[>0>,>0>,>0>,>0>,>0>,>0>]]> g>=> Graph(graph)> source>=> 0>; sink>=> 5> > print> (>'The maximum possible flow is %d '> %> g.FordFulkerson(source, sink))> # This code is contributed by Neelam Yadav> |
algoritem za razvrščanje vstavljanja
>
>
C#
// C# program for implementation> // of Ford Fulkerson algorithm> using> System;> using> System.Collections.Generic;> public> class> MaxFlow {> >static> readonly> int> V = 6;>// Number of vertices in> >// graph> >/* Returns true if there is a path> >from source 's' to sink 't' in residual> >graph. Also fills parent[] to store the> >path */> >bool> bfs(>int>[, ] rGraph,>int> s,>int> t,>int>[] parent)> >{> >// Create a visited array and mark> >// all vertices as not visited> >bool>[] visited =>new> bool>[V];> >for> (>int> i = 0; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited List |
>
>
Javascript
mylivecricket za kriket v živo
> // Javascript program for implementation of Ford> // Fulkerson algorithm> // Number of vertices in graph> let V = 6;> // Returns true if there is a path from source> // 's' to sink 't' in residual graph. Also> // fills parent[] to store the path> function> bfs(rGraph, s, t, parent)> {> > >// Create a visited array and mark all> >// vertices as not visited> >let visited =>new> Array(V);> >for>(let i = 0; i visited[i] = false; // Create a queue, enqueue source vertex // and mark source vertex as visited let queue = []; queue.push(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.length != 0) { let u = queue.shift(); for(let v = 0; v { if (visited[v] == false && rGraph[u][v]>0) { // Če najdemo povezavo s ponornim // vozliščem, potem v BFS // ni več smisla. Samo nastaviti moramo njegov nadrejeni // in lahko vrnemo true if (v == t) { nadrejeni [ v] = u; vrni resnico; } queue.push(v); nadrejeni [v] = u; obiskano [v] = res; } } } // Nismo dosegli ponora v BFS, ki se začne // iz vira, zato vrni false return false; } // Vrne največji pretok od s do t v // danem grafu funkcija fordFulkerson(graph, s, t) { let u, v; // Ustvarite rezidualni graf in izpolnite // rezidualni graf z danimi zmogljivostmi // v izvirnem grafu kot preostale // zmogljivosti v rezidualnem grafu // Rezidualni graf, kjer rGraph[i][j] // označuje preostalo zmogljivost roba / / od i do j (če obstaja rob. // Če je rGraph[i][j] 0, potem ga // ni) let rGraph = new Array(V); for(u = 0; u { rGraph[u] = new Array(V); for(v = 0; v rGraph[u][v] = graph[u][v]; } // To polje je zapolnjeno z BFS in za shranjevanje poti let parent = new Array(V); // Na začetku ni pretoka pusti max_flow = 0; // Povečaj tok, medtem ko obstaja pot od izvora do ponora while (bfs(rGraph, s, t) , nadrejeni) { // Najdi najmanjšo preostalo zmogljivost robov // vzdolž poti, ki jo zapolnjuje BFS. Najdi pot. MAX_VALUE; ; v != s; v = parent[v]; path_flow = Math.min(path_flow, rGraph[u]); obrnite robove vzdolž poti for(v = t; v != s; v = parent[v]) { u = parent[v]; rGraph[u][v] -= path_flow; rGraph[v][u] + = path_flow; } // Dodajanje celotnega toka max_flow; // Vrnitev celotnega toka max_flow; // Ustvarimo graf, prikazan v zgornjem primeru, let graph = [ 0 , 16, 13, 0, 0, 0 ], [ 0, 0, 10, 12, 0, 0 ], [ 0, 4, 0, 0, 14, 0 ], [ 0, 0, 9, 0, 0 , 20], [0, 0, 0, 7, 0, 4], [0, 0, 0, 0, 0, 0]]; document.write('Največji možni pretok je ' + fordFulkerson(graf, 0, 5)); // To kodo je prispeval avanitrachhadiya2155> |
>
>Izhod
The maximum possible flow is 23>
Časovna zapletenost: O(|V| * E^2) , kjer je E število robov in V število oglišč.
Prostorska kompleksnost: O(V), ko smo ustvarili čakalno vrsto.
Zgornja izvedba algoritma Ford Fulkerson se imenuje Algoritem Edmonds-Karp . Zamisel Edmonds-Karpa je uporaba BFS v izvedbi Ford Fulkerson, saj BFS vedno izbere pot z najmanjšim številom robov. Ko se uporablja BFS, se lahko časovna kompleksnost v najslabšem primeru zmanjša na O(VE2). Zgornja izvedba uporablja predstavitev matrike sosednosti, čeprav BFS vzame O(V2) čas, je časovna kompleksnost zgornje izvedbe O(EV3) (Glej knjiga CLRS za dokazilo o časovni zahtevnosti)
To je pomemben problem, saj se pojavlja v številnih praktičnih situacijah. Primeri vključujejo maksimiranje transporta z danimi omejitvami prometa, maksimiranje pretoka paketov v računalniških omrežjih.
Dincov algoritem za največji pretok.
Vaja:
Spremenite zgornjo izvedbo tako, da bo delovala v O(VE2) čas.
