A števec je naprava, ki shranjuje (in včasih prikazuje), kolikokrat se je zgodil določen dogodek ali proces, pogosto v povezavi s signalom ure. Števci se uporabljajo v digitalni elektroniki za namene štetja, saj lahko štejejo določene dogodke, ki se dogajajo v vezju. Na primer, v števcu UP števec poveča število za vsak naraščajoči rob ure. Ne samo štetje, števec lahko sledi določenemu zaporedju, ki temelji na naši zasnovi, kot vsako naključno zaporedje 0,1,3,2… Lahko se oblikujejo tudi s pomočjo japonk. Uporabljajo se kot frekvenčni delilniki, kjer se frekvenca dane oblike impulznega valovanja deli. Števci so zaporedno vezje, ki šteje število impulzov, lahko v binarni kodi ali BCD obliki. Glavne lastnosti števca so časovna razporeditev, zaporedje in štetje. Števec deluje v dveh načinih
Gor števec
Spodnji pult
Protiklasifikacija
Števci so na splošno razdeljeni v dve kategoriji
- Asinhroni števec
- Sinhroni števec
1. Asinhroni števec
V asinhronem števcu ne uporabljamo univerzalne ure, samo prvi flip flop poganja glavna ura, vhod ure preostalega naslednjega flip flopa pa izhod prejšnjih flip flopov. To lahko razumemo z naslednjim diagramom -
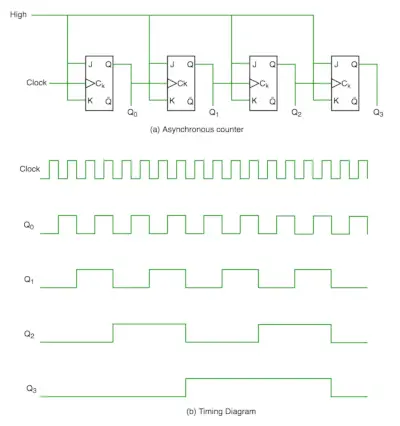
Iz časovnega diagrama je razvidno, da se Q0 spremeni takoj, ko naletimo na naraščajoči rob taktnega impulza, Q1 se spremeni, ko naletimo na naraščajoči rob Q0 (ker je Q0 kot taktni impulz za drugi flip flop) in tako naprej. Na ta način se ustvarjajo valovi skozi Q0, Q1, Q2, Q3, zato se imenuje tudi Števec RIPPLE in serijski števec. Števec valovanja je kaskadna razporeditev flip flopov, kjer izhod enega flip flopa poganja taktni vhod naslednjega flip flopa.
2. Sinhroni števec
Za razliko od asinhronega števca ima sinhroni števec eno globalno uro, ki poganja vsak flip flop, tako da se izhod spreminja vzporedno. Ena prednost sinhronega števca pred asinhronim števcem je, da lahko deluje na višji frekvenci kot asinhroni števec, ker nima kumulativne zakasnitve, ker je enaka ura dana vsaki flip flop. Imenuje se tudi vzporedni števec.
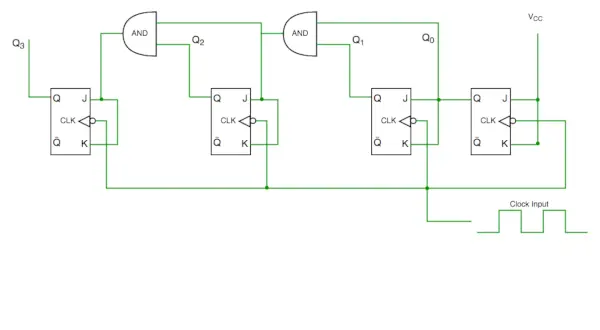
Sinhronsko števčno vezje
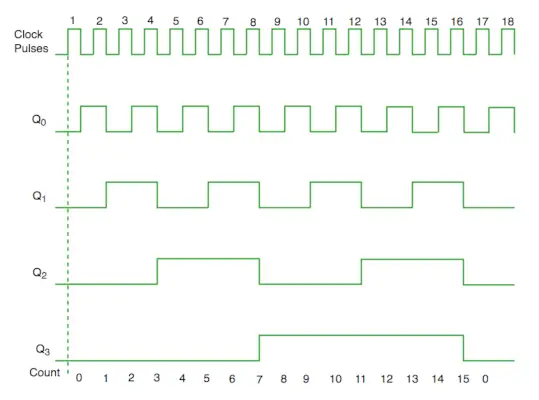
Časovni diagram sinhronskega števca
Iz diagrama vezja vidimo, da bit Q0 daje odziv na vsak padajoči rob takta, medtem ko je Q1 odvisen od Q0, Q2 je odvisen od Q1 in Q0, Q3 je odvisen od Q2, Q1 in Q0.
Desetletni števec
Števec desetletja šteje deset različnih stanj in se nato ponastavi na začetna stanja. Preprost desetletni števec bo štel od 0 do 9, vendar lahko izdelamo tudi desetletne števce, ki lahko gredo skozi poljubnih deset stanj med 0 in 15 (za 4-bitni števec).
| Urni utrip | Q3 | Q2 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 0 | 0 | 0 | 0 |
Tabela resnic za preprost števec desetletij
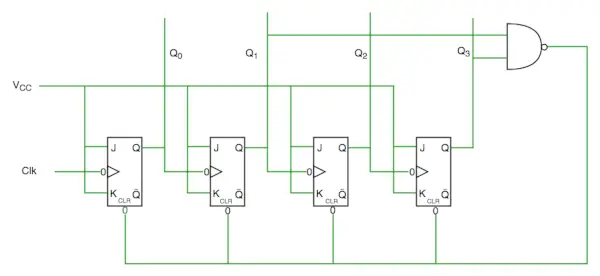
Shema vezja desetletnega števca
Iz diagrama vezja vidimo, da smo uporabili vrata nand za Q3 in Q1 in to dovajali za brisanje vhodne vrstice, ker je binarna predstavitev 10—
1010
In vidimo, da sta Q3 in Q1 tukaj 1, če damo NAND teh dveh bitov za brisanje vhoda, bo števec počiščen pri 10 in spet začne od začetka.
Pomembna točka : Število japonk, uporabljenih v števcu, je vedno večje od enakega ( dnevnik2n ), kjer je n=število stanj v števcu.
Nekatera vprašanja iz prejšnjih let o števcih
Q1. Razmislite o delni izvedbi 2-bitnega števca z uporabo T flip-flopov po zaporedju 0-2-3-1-0, kot je prikazano spodaj
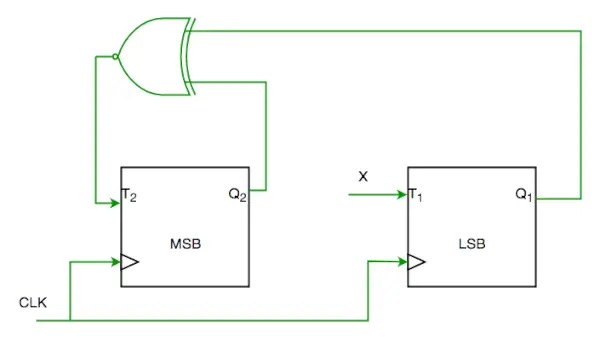
Za dokončanje vezja mora biti vhod X
(A) Q2?
(B) Q2 + Q1
(C) (Q1 ? Q2)'
(D) Q1? Q2 (GATE-CS-2004)
rešitev:
Iz vezja vidimo
T1=XQ1’+X’Q1—-(1)
IN
T2=(Q2 ? Q1)'—-(2)
IN ŽELENI IZHOD JE 00->10->11->01->00
TAKO NAJ BO X Q1Q2'+Q1'Q2 ZADOVOLJIV 1 IN 2.
TOREJ ANS JE (D) DEL.
Q2. Funkcije krmilnega signala 4-bitnega binarnega števca so podane spodaj (kjer je X vseeno)
Števec je povezan na naslednji način:
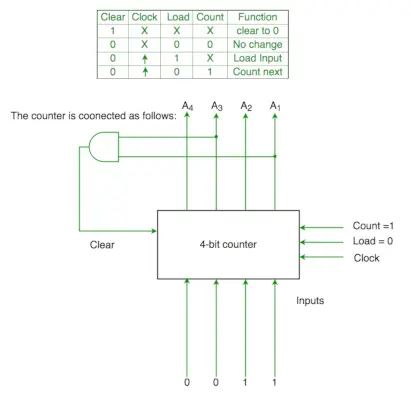
Predpostavimo, da so zakasnitve števca in vrat zanemarljive. Če se števec začne pri 0, potem kroži skozi naslednje zaporedje:
(A) 0,3,4
(B) 0,3,4,5
(C) 0,1,2,3,4
(D) 0,1,2,3,4,5 (GATE-CS-2007)
rešitev:
Začetno A1 A2 A3 A4 =0000
Clr=A1 in A3
Torej, ko sta A1 in A3 oba 1, gre spet na 0000
Zato 0000(začet.) -> 0001(A1 in A3=0)->0010 (A1 in A3=0) -> 0011(A1 in A3=0) -> 0100 ( A1 in A3=1 )[ jasen pogoj izpolnjen] ->0000(začet.), tako da gre skozi 0->1->2->3->4
An je (C) del.
razčlenjevanje niza v int
Kviz o digitalni logiki
Članek prispeval Anuj Batham,
