KOSINUS PODOBNOSTI

Predpogoj – podatkovno rudarjenje, mera podobnosti se nanaša na razdaljo z dimenzijami, ki predstavljajo lastnosti podatkovnega objekta v naboru podatkov. Če je ta razdalja manjša, bo stopnja podobnosti visoka, ko pa je razdalja velika, bo stopnja podobnosti nizka. Nekatera priljubljena merila podobnosti so –

Evklidska razdalja.
Razdalja Manhattan.
Jaccardova podobnost.
Razdalja Minkowski.
Kosinus podobnosti.

Kosinusna podobnost je metrika, ki pomaga pri določanju, kako podobni so si podatkovni objekti ne glede na njihovo velikost. Podobnost med dvema stavkoma v Pythonu lahko izmerimo s kosinusno podobnostjo. Pri kosinusni podobnosti se podatkovni objekti v naboru podatkov obravnavajo kot vektor. Formula za iskanje podobnosti kosinusa med dvema vektorjema je –

(x, y) = x . y / ||x||  ||y||>

kje,

||in||

||in||

Primer: Razmislite o primeru, da ugotovite podobnost med dvema vektorjema – 'x' in 'in' , z uporabo kosinusne podobnosti. Vektor 'x' ima vrednosti, x = {3, 2, 0, 5} Vektor 'y' ima vrednosti, y = {1, 0, 0, 0} Formula za izračun kosinusne podobnosti je: (x, y) = x. y / ||x|| ||in||

x . y = 3*1 + 2*0 + 0*0 + 5*0 = 3 ||x|| = √ (3)^2 + (2)^2 + (0)^2 + (5)^2 = 6.16 ||y|| = √ (1)^2 + (0)^2 + (0)^2 + (0)^2 = 1 ∴ (x, y) = 3 / (6.16 * 1) = 0.49>

Razlika med vektorjema 'x' in 'y' je podana z -

java predmet v json

∴ (x, y) = 1 - (x, y) = 1 - 0.49 = 0.51>

Kosinusna podobnost med dvema vektorjema se meri v 'θ'.
Če je θ = 0°, se vektorja 'x' in 'y' prekrivata, kar dokazuje, da sta si podobna.
Če je θ = 90°, sta vektorja 'x' in 'y' različna.

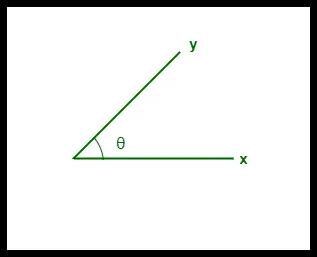
Kosinus Podobnost med dvema vektorjema

Prednosti:

Kosinusna podobnost je koristna, saj imata dva podobna podatkovna objekta zaradi velikosti lahko še vedno manjši kot, tudi če sta dva podobna podatkovna objekta oddaljena za evklidsko razdaljo. Manjši je kot, večja je podobnost.
Ko je narisana na večdimenzionalnem prostoru, kosinusna podobnost zajame orientacijo (kot) podatkovnih objektov in ne velikosti.