V realnem svetu nimajo vsi podatki, s katerimi delamo, ciljne spremenljivke. Tovrstnih podatkov ni mogoče analizirati z algoritmi za nadzorovano učenje. Potrebujemo pomoč nenadzorovanih algoritmov. Ena najbolj priljubljenih vrst analize pri nenadzorovanem učenju je segmentacijo strank za ciljane oglase ali v medicinskem slikanju za iskanje neznanih ali novih okuženih območij in veliko drugih primerov uporabe, o katerih bomo podrobneje razpravljali v tem članku.
Kazalo
linux free ipconfig
- Kaj je grozdenje?
- Vrste združevanja v gruče
- Uporaba združevanja v gruče
- Vrste algoritmov združevanja v gruče
- Aplikacije grozdenja na različnih področjih:
- Pogosto zastavljena vprašanja (FAQ) o grozdenju
Kaj je grozdenje?
Naloga združevanja podatkovnih točk glede na njihovo medsebojno podobnost se imenuje združevanje v gruče ali analiza gruč. Ta metoda je opredeljena pod vejo Učenje brez nadzora , katerega cilj je pridobivanje vpogledov iz neoznačenih podatkovnih točk, to je za razliko od nadzorovano učenje nimamo ciljne spremenljivke.
Cilj združevanja v gruče je oblikovanje skupin homogenih podatkovnih točk iz heterogenega nabora podatkov. Podobnost oceni na podlagi metrike, kot je evklidska razdalja, kosinusna podobnost, manhattanska razdalja itd., nato pa združi točke z najvišjo oceno podobnosti.
Na primer, na spodnjem grafu lahko jasno vidimo, da obstajajo 3 krožne skupine, ki se oblikujejo na podlagi razdalje.
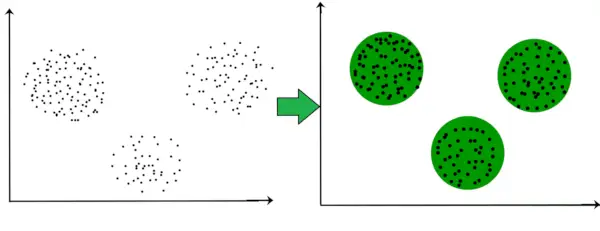
Zdaj ni nujno, da morajo biti oblikovani grozdi okrogle oblike. Oblika grozdov je lahko poljubna. Obstaja veliko algoritmov, ki dobro delujejo pri zaznavanju skupin poljubnih oblik.
Na primer, v spodnjem grafu lahko vidimo, da oblikovani grozdi niso krožne oblike.

četrtletja v letu
Vrste združevanja v gruče
Na splošno obstajata dve vrsti združevanja v gruče, ki ju je mogoče izvesti za združevanje podobnih podatkovnih točk:
- Trdo združevanje v gruče: Pri tej vrsti združevanja v gruče vsaka podatkovna točka v celoti pripada gruči ali ne. Na primer, recimo, da obstajajo 4 podatkovne točke in jih moramo združiti v 2 gruči. Tako bo vsaka podatkovna točka pripadala skupini 1 ali skupini 2.
| Podatkovne točke | Grozdi |
|---|---|
| A | C1 |
| B | C2 |
| C | C2 |
| D | C1 |
- Mehko združevanje v gruče: Pri tej vrsti združevanja v gruče se namesto dodeljevanja vsake podatkovne točke v ločeno gručo oceni verjetnost ali verjetnost, da je ta točka ta gruča. Na primer, recimo, da obstajajo 4 podatkovne točke in jih moramo združiti v 2 gruči. Tako bomo ocenili verjetnost, da podatkovna točka pripada obema gručema. Ta verjetnost se izračuna za vse podatkovne točke.
| Podatkovne točke | Verjetnost C1 | Verjetnost C2 |
| A | 0,91 | 0,09 |
| B | 0,3 | 0,7 |
| C | 0,17 | 0,83 |
| D | 1 | 0 |
Uporaba združevanja v gruče
Preden začnemo z vrstami algoritmov za združevanje v gruče, si bomo ogledali primere uporabe algoritmov za združevanje v gruče. Algoritmi združevanja v gruče se večinoma uporabljajo za:
- Delitev trga – Podjetja uporabljajo združevanje v skupine za združevanje svojih strank in uporabo ciljanih oglasov, da pritegnejo več občinstva.
- Analiza družbenega omrežja – Spletna mesta družbenih medijev uporabljajo vaše podatke, da razumejo vaše vedenje pri brskanju in vam zagotovijo ciljana priporočila prijateljev ali priporočila glede vsebine.
- Medicinsko slikanje – zdravniki uporabljajo združevanje v skupine, da odkrijejo obolela področja na diagnostičnih slikah, kot so rentgenski žarki.
- Odkrivanje nepravilnosti – Za iskanje izstopajočih vrednosti v toku nabora podatkov v realnem času ali napovedovanje goljufivih transakcij lahko uporabimo združevanje v gruče, da jih identificiramo.
- Poenostavite delo z velikimi nabori podatkov – vsaka gruča dobi ID gruče po končanem združevanju v gruče. Zdaj lahko zmanjšate celoten nabor funkcij nabora funkcij v njegov ID gruče. Združevanje v gruče je učinkovito, če lahko predstavlja zapleten primer z enostavnim ID-jem gruče. Z uporabo istega načela lahko združevanje podatkov v gruče poenostavi kompleksne nize podatkov.
Obstaja veliko več primerov uporabe za združevanje v gruče, vendar obstaja nekaj glavnih in pogostih primerov uporabe združevanja v gruče. V nadaljevanju bomo razpravljali o algoritmih združevanja v gruče, ki vam bodo pomagali pri izvedbi zgornjih nalog.
Vrste algoritmov združevanja v gruče
Na površinski ravni združevanje v gruče pomaga pri analizi nestrukturiranih podatkov. Grafiranje, najkrajša razdalja in gostota podatkovnih točk je nekaj elementov, ki vplivajo na oblikovanje grozdov. Združevanje v gruče je postopek ugotavljanja, kako sorodni so predmeti na podlagi metrike, imenovane mera podobnosti. Meritve podobnosti je lažje najti v manjših nizih funkcij. Težje je ustvariti mere podobnosti, ko se število funkcij poveča. Odvisno od vrste algoritma združevanja v gruče, ki se uporablja pri rudarjenju podatkov, se za združevanje podatkov iz naborov podatkov uporablja več tehnik. V tem delu so opisane tehnike združevanja v gruče. Različne vrste algoritmov združevanja v gruče so:
- Centroidno združevanje v gruče (metode particioniranja)
- Združevanje v gruče na podlagi gostote (metode na podlagi modela)
- Združevanje na podlagi povezljivosti (hierarhično združevanje)
- Gručenje na podlagi distribucije
Na kratko bomo pregledali vsako od teh vrst.
1. Metode particioniranja so najlažji algoritmi za združevanje v gruče. Podatkovne točke združujejo glede na njihovo bližino. Na splošno je mera podobnosti, izbrana za te algoritme, Evklidska razdalja, Manhattanska razdalja ali razdalja Minkowskega. Nabori podatkov so ločeni v vnaprej določeno število gruč, na vsako gručo pa se sklicuje vektor vrednosti. V primerjavi z vektorsko vrednostjo spremenljivka vhodnih podatkov ne pokaže nobene razlike in se pridruži gruči.
Primarna pomanjkljivost teh algoritmov je zahteva, da določimo število gruč, k, intuitivno ali znanstveno (z uporabo metode Elbow), preden kateri koli sistem za strojno učenje v gruče začne dodeljevati podatkovne točke. Kljub temu je še vedno najbolj priljubljena vrsta združevanja v gruče. K-pomeni in K-medoidi združevanje v gruče je nekaj primerov te vrste združevanja v gruče.
2. Združevanje v gruče na podlagi gostote (metode na podlagi modela)
Gruččenje na podlagi gostote, metoda, ki temelji na modelu, najde skupine na podlagi gostote podatkovnih točk. V nasprotju z združevanjem v gruče na podlagi centroida, ki zahteva, da je število gruč vnaprej določeno in je občutljivo na inicializacijo, združevanje v gruče na podlagi gostote samodejno določi število gruč in je manj dovzetno za začetne položaje. Odlični so pri rokovanju z gručami različnih velikosti in oblik, zaradi česar so idealni za nabore podatkov z nepravilno oblikovanimi ali prekrivajočimi se gručami. Te metode upravljajo z gostimi in redkimi podatkovnimi regijami z osredotočanjem na lokalno gostoto in lahko razlikujejo grozde z različnimi morfologijami.
Nasprotno pa ima združevanje na osnovi centroida, tako kot k-means, težave pri iskanju skupin poljubnih oblik. Zaradi prednastavljenega števila zahtev za gruče in izjemne občutljivosti na začetno pozicioniranje centroidov se lahko rezultati razlikujejo. Poleg tega težnja pristopov, ki temeljijo na centroidu, da proizvedejo sferične ali konveksne grozde, omejuje njihovo zmožnost obvladovanja zapletenih ali nepravilno oblikovanih grozdov. Skratka, združevanje v gruče na podlagi gostote premaguje pomanjkljivosti tehnik, ki temeljijo na centroidu, tako da avtonomno izbira velikosti gruč, je odporno na inicializacijo in uspešno zajema grozde različnih velikosti in oblik. Najbolj priljubljen algoritem združevanja v gruče, ki temelji na gostoti, je DBSCAN .
3. Združevanje na podlagi povezljivosti (hierarhično združevanje)
Metoda za sestavljanje povezanih podatkovnih točk v hierarhične gruče se imenuje hierarhično združevanje v gruče. Vsaka podatkovna točka se na začetku upošteva kot ločena gruča, ki se nato združi z najbolj podobnimi gručami v eno veliko gručo, ki vsebuje vse podatkovne točke.
Pomislite, kako lahko uredite zbirko predmetov glede na to, kako podobni so si. Vsak objekt se pri uporabi hierarhičnega združevanja v gruče, ki ustvari dendrogram, drevesu podobno strukturo, začne kot lastna gruča na dnu drevesa. Najbližji pari grozdov se nato združijo v večje grozde, potem ko algoritem preuči, kako podobni so predmeti drug drugemu. Ko je vsak objekt v eni gruči na vrhu drevesa, je postopek združevanja končan. Raziskovanje različnih stopenj razdrobljenosti je ena izmed zabavnih stvari pri hierarhičnem združevanju v gruče. Če želite pridobiti določeno število grozdov, lahko izberete rezanje dendrogram na določeni višini. Bolj kot sta si podobna dva predmeta znotraj gruče, bližje sta si. To je primerljivo z razvrščanjem predmetov glede na njihova družinska drevesa, kjer so najbližji sorodniki združeni, širše veje pa pomenijo bolj splošne povezave. Obstajata dva pristopa za hierarhično združevanje v gruče:
git pull sintaksa
- Razdeljujoče grozdenje : Sledi pristopu od zgoraj navzdol, tukaj menimo, da so vse podatkovne točke del ene velike skupine, nato pa se ta skupina razdeli na manjše skupine.
- Aglomerativno združevanje : Sledi pristopu od spodaj navzgor, pri čemer vse podatkovne točke obravnavamo kot del posameznih grozdov, nato pa te grozde združimo v en velik grozd z vsemi podatkovnimi točkami.
4. Gručenje na podlagi distribucije
Z združevanjem v gruče na podlagi porazdelitve se podatkovne točke generirajo in organizirajo glede na njihovo nagnjenost, da spadajo v isto verjetnostno porazdelitev (kot je Gaussova, binomska ali druga) znotraj podatkov. Podatkovni elementi so združeni z uporabo verjetnostne distribucije, ki temelji na statističnih distribucijah. Vključeni so podatkovni objekti, za katere obstaja večja verjetnost, da bodo v gruči. Manjša je verjetnost, da bo podatkovna točka vključena v gručo, čim dlje je od osrednje točke gruče, ki obstaja v vsaki gruči.
Pomembna pomanjkljivost pristopov, ki temeljijo na gostoti in mejah, je potreba po a priori določitvi gruč za nekatere algoritme in predvsem definicija oblike gruč za večino algoritmov. Izbrano mora biti vsaj eno uglaševanje ali hiperparameter, in čeprav bi moralo biti to preprosto, bi lahko imela napačna izbira nepričakovane posledice. Združevanje v gruče na podlagi porazdelitve ima nedvomno prednost pred pristopi združevanja v gruče na podlagi bližine in centroida v smislu prilagodljivosti, natančnosti in strukture gruče. Ključno vprašanje je, da bi se izognili prekomerno opremljanje , številne metode združevanja v gruče delujejo samo s simuliranimi ali izdelanimi podatki ali kadar večina podatkovnih točk zagotovo pripada prednastavljeni porazdelitvi. Najbolj priljubljen algoritem združevanja v gruče, ki temelji na distribuciji, je Gaussov model mešanice .
Aplikacije grozdenja na različnih področjih:
- Trženje: Uporablja se lahko za karakterizacijo in odkrivanje segmentov strank za namene trženja.
- Biologija: Lahko se uporablja za razvrščanje med različne vrste rastlin in živali.
- Knjižnice: Uporablja se pri združevanju različnih knjig na podlagi tem in informacij.
- Zavarovanje: Uporablja se za potrditev strank, njihovih politik in prepoznavanje goljufij.
- Načrtovanje mesta: Uporablja se za sestavljanje skupin hiš in preučevanje njihovih vrednosti na podlagi njihovih geografskih lokacij in drugih prisotnih dejavnikov.
- Študije potresov: S spoznavanjem potresno prizadetih območij lahko določimo nevarna območja.
- Obdelava slik : Združevanje v gruče lahko uporabite za združevanje podobnih slik, razvrščanje slik na podlagi vsebine in prepoznavanje vzorcev v slikovnih podatkih.
- Genetika: Združevanje v skupine se uporablja za združevanje genov, ki imajo podobne vzorce izražanja, in prepoznavanje genskih mrež, ki delujejo skupaj v bioloških procesih.
- Finance: Grozdenje se uporablja za identifikacijo tržnih segmentov na podlagi vedenja kupcev, prepoznavanje vzorcev v podatkih o delniških trgih in analizo tveganja v naložbenih portfeljih.
- Storitev za stranke: Grozdenje se uporablja za združevanje poizvedb in pritožb strank v kategorije, prepoznavanje skupnih težav in razvoj ciljno usmerjenih rešitev.
- Proizvodnja : Grozdenje se uporablja za združevanje podobnih izdelkov skupaj, optimizacijo proizvodnih procesov in prepoznavanje napak v proizvodnih procesih.
- Medicinska diagnoza: Združevanje v skupine se uporablja za združevanje bolnikov s podobnimi simptomi ali boleznimi, kar pomaga pri postavljanju natančnih diagnoz in prepoznavanju učinkovitega zdravljenja.
- Odkrivanje goljufij: Združevanje v skupine se uporablja za prepoznavanje sumljivih vzorcev ali anomalij v finančnih transakcijah, kar lahko pomaga pri odkrivanju goljufij ali drugih finančnih kaznivih dejanj.
- Analiza prometa: Združevanje v gruče se uporablja za združevanje podobnih vzorcev prometnih podatkov, kot so ure konic, poti in hitrosti, kar lahko pomaga pri izboljšanju načrtovanja prevoza in infrastrukture.
- Analiza socialnih omrežij: Grozdenje se uporablja za identifikacijo skupnosti ali skupin znotraj socialnih omrežij, kar lahko pomaga pri razumevanju družbenega vedenja, vpliva in trendov.
- Spletna varnost: Združevanje v gruče se uporablja za združevanje podobnih vzorcev omrežnega prometa ali vedenja sistema, kar lahko pomaga pri odkrivanju in preprečevanju kibernetskih napadov.
- Analiza podnebja: Združevanje v skupine se uporablja za združevanje podobnih vzorcev podnebnih podatkov, kot so temperatura, padavine in veter, kar lahko pomaga pri razumevanju podnebnih sprememb in njihovega vpliva na okolje.
- Športna analiza: Združevanje v skupine se uporablja za združevanje podobnih vzorcev podatkov o uspešnosti igralcev ali ekip, kar lahko pomaga pri analizi prednosti in slabosti igralca ali ekipe ter sprejemanju strateških odločitev.
- Analiza kriminala: Združevanje v skupine se uporablja za združevanje podobnih vzorcev podatkov o kriminalu, kot so lokacija, čas in vrsta, kar lahko pomaga pri prepoznavanju žarišč kriminala, napovedovanju prihodnjih trendov kriminala in izboljšanju strategij za preprečevanje kriminala.
Zaključek
V tem članku smo razpravljali o grozdenju, njegovih vrstah in aplikacijah v resničnem svetu. Pri nenadzorovanem učenju je treba zajeti veliko več in analiza grozdov je le prvi korak. Ta članek vam lahko pomaga začeti z algoritmi združevanja v gruče in vam pomaga pridobiti nov projekt, ki ga lahko dodate v svoj portfelj.
Pogosto zastavljena vprašanja (FAQ) o grozdenju
V. Kateri je najboljši način združevanja v gruče?
10 najboljših algoritmov za združevanje v gruče je:
- K-pomeni grozdenje
- Hierarhično združevanje v gruče
- DBSCAN (prostorsko združevanje aplikacij s šumom na podlagi gostote)
- Gaussovi mešani modeli (GMM)
- Aglomerativno združevanje
- Spektralno združevanje
- Srednje premikanje v gruče
- Razmnoževanje afinitete
- OPTIKA (naročanje točk za prepoznavanje strukture združevanja)
- Birch (Uravnoteženo iterativno zmanjševanje in združevanje v gruče z uporabo hierarhij)
V. Kakšna je razlika med združevanjem v gruče in razvrščanjem?
Glavna razlika med združevanjem v gruče in klasifikacijo je v tem, da je klasifikacija nadzorovan učni algoritem, združevanje v gruče pa nenadzorovan učni algoritem. To pomeni, da uporabimo združevanje v skupine za tiste nize podatkov, ki nimajo ciljne spremenljivke.
V. Kakšne so prednosti analize združevanja v gruče?
Podatke je mogoče organizirati v smiselne skupine z uporabo močnega analitičnega orodja analize grozdov. Uporabite ga lahko za natančno določanje segmentov, iskanje skritih vzorcev in izboljšanje odločitev.
V. Kateri je najhitrejši način združevanja v gruče?
Združevanje v gruče K-means pogosto velja za najhitrejšo metodo združevanja v gruče zaradi svoje preprostosti in računalniške učinkovitosti. Iterativno dodeljuje podatkovne točke najbližjemu centroidu gruče, zaradi česar je primeren za velike nabore podatkov z nizko dimenzionalnostjo in zmernim številom gruč.
V. Kakšne so omejitve združevanja v gruče?
Omejitve združevanja v gruče vključujejo občutljivost na začetne pogoje, odvisnost od izbire parametrov, težave pri določanju optimalnega števila gruč in izzive pri ravnanju z visokodimenzionalnimi ali šumnimi podatki.
številčenje abecede
V. Od česa je odvisna kakovost rezultata združevanja v gruče?
Kakovost rezultatov gručenja je odvisna od dejavnikov, kot so izbira algoritma, metrika razdalje, število gruč, metoda inicializacije, tehnike predprocesiranja podatkov, metrike vrednotenja gruč in poznavanje domene. Ti elementi skupaj vplivajo na učinkovitost in natančnost rezultata združevanja v gruče.
