Dvojiški številski sistem je številski sistem, ki se uporablja za predstavitev različnih števil z uporabo samo dveh simbolov 0 in 1. Beseda dvojiško je izpeljana iz besede bi, ki pomeni dva. Zato se ta številski sistem imenuje binarni številski sistem. Tako je binarni številski sistem sistem, ki ima samo dva simbola.
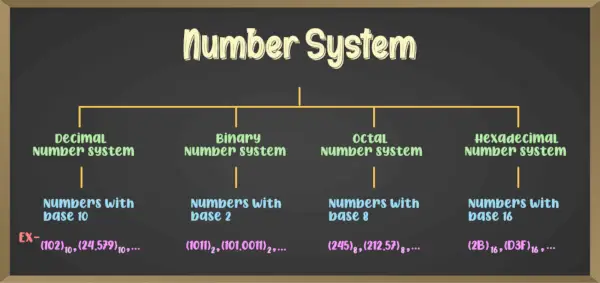
Na splošno obstaja več vrst številskih sistemov in med njimi so štirje glavni,
- Dvojiški številski sistem (številski sistem z osnovo 2)
- Osmiški številski sistem (številski sistem z osnovo 8)
- Decimalni številski sistem (številski sistem z osnovo 10)
- Šestnajstiški številski sistem (številski sistem z osnovo 16)
Tukaj se bomo samo naučili o binarnem številskem sistemu. Ta številski sistem je zelo uporaben za razlago nalog računalniku. V binarnem številskem sistemu imamo dve stanji 0 in 1 in ti dve stanji sta predstavljeni z dvema stanjima tranzistorja. Če tok teče skozi tranzistor, potem računalnik prebere 1 in če toka ni v tranzistorju, potem prebere 0. Tako izmenični tok računalnik prebere binarni številski sistem. Vsako števko v binarnem številskem sistemu imenujemo bit.
V tem članku bomo podrobno spoznali binarni številski sistem, pretvorbo binarnega številskega sistema, binarno tabelo, delovanje binarnih števil, primere in drugo.
Kazalo
- Dvojiški številski sistem
- Tabela binarnih števil
- Binarno v decimalno pretvorbo
- Decimalno v binarno pretvorbo
- Aritmetične operacije nad binarnimi števili
- Komplement 1 in 2 binarnega števila
- Uporaba binarnega številskega sistema
- Primer binarnega številskega sistema
Dvojiški številski sistem
Binarni številski sistem je številski sistem, v katerem uporabljamo dve števki 0 in 1 za izvajanje vseh potrebnih operacij. V binarnem številskem sistemu imamo osnovo 2. Osnovo binarnega številskega sistema imenujemo tudi radiks številski sistem .
V dvojiškem številskem sistemu predstavljamo število kot,
- (11001)2
V zgornjem primeru je podano binarno število, katerega osnova je 2. V binarnem številskem sistemu se vsaka cifra imenuje bit. V zgornjem primeru je 5 števk.
Tabela binarnih števil
| Decimalno število | Binarno število | Decimalno število | Binarno število |
|---|---|---|---|
| 1 | 001 | enajst | 1011 |
| 2 | 010 | 12 | 1100 |
| 3 | 011 | 13 | 1101 |
| 4 | 100 | 14 | 1110 |
| 5 | 101 | petnajst | 1111 |
| 6 | 110 | 16 | 10000 |
| 7 | 111 | 17 | 10001 |
| 8 | 1000 | 18 | 10010 |
| 9 | 1001 | 19 | 10011 |
| 10 v nizu v Javi | 1010 | dvajset | 10100 |
Binarno v decimalno pretvorbo
Dvojiško število pretvorimo v decimalno število tako, da vsako števko binarnega števila pomnožimo s potenco 1 ali 0 na ustrezno potenco 2. Recimo, da ima binarno število n števk, B = an-1…a3a2a1a0. Zdaj je ustrezno decimalno število podano kot
D = (a n-1 ×2 n-1 ) +…+(a 3 ×2 3 ) + (a 2 ×2 2 ) + (a 1 ×2 1 ) + (a 0 ×2 0 )
Oglejmo si primer, da bomo bolje razumeli koncept.
Primer: Pretvori (10011) 2 na decimalno število.
rešitev:
Dano binarno število je (10011)2.
(10011)2= (1 × 24) + (0 × 23) + (0 × 22) + (1 × 21) + (1 × 20)
= 16 + 0 + 0 + 2 + 1 = (19)10
Torej binarno število (10011)2je izražen kot (19)10.
Decimalno v binarno pretvorbo
Decimalno število pretvorimo v binarno število tako, da dano decimalno število neprekinjeno delimo z 2, dokler ne dobimo količnika 1, števila pa pišemo od navzdol navzgor.
Oglejmo si primer, da bomo bolje razumeli koncept.
Primer: Pretvori (28) 10 v binarno število.
rešitev:
Zato (28)10je izražen kot (11100)2.
Aritmetične operacije nad binarnimi števili
Z binarnimi števili lahko enostavno izvajamo različne operacije. Različne aritmetične operacije na binarnem številu vključujejo,
- Binarno seštevanje
- Binarno odštevanje
- Binarno množenje
- Binarna delitev
Zdaj pa se o tem podrobneje naučimo.
Binarno seštevanje
Tudi rezultat seštevanja dveh binarnih števil je binarno število. Da dobimo rezultat seštevanja dveh binarnih števil, moramo števko dvojiških števil sešteti za števko. Spodnja tabela prikazuje pravilo binarnega seštevanja.
| Binarno število (1) | Binarno število (2) | Dodatek | Nositi |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Binarno odštevanje
Tudi rezultat odštevanja dveh binarnih števil je binarno število. Da dobimo rezultat odštevanja dveh binarnih števil, moramo števko dvojiških števil odšteti za števko. Spodnja tabela prikazuje pravilo binarnega odštevanja.
| Binarno število (1) | Binarno število (2) | Odštevanje | Izposodite si |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
Binarno množenje
Postopek množenja binarnih števil je podoben množenju decimalnih števil. Pravila za množenje katerih koli dveh binarnih števil so podana v tabeli,
| Binarno število (1) | Binarno število (2) | Množenje |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Binarna delitev
The metoda delitve za binarna števila je podobna metodi deljenja decimalnih števil. Oglejmo si primer, da bomo bolje razumeli koncept.
Primer: Razdeli (101101) 2 avtor (110) 2
rešitev:
Komplement 1 in 2 binarnega števila
- 1 komplement binarnega števila dobimo z obračanjem števk binarnega števila.
Primer: poiščite komplement 1 od (10011) 2 .
rešitev:
Dano binarno število je (10011)2
Zdaj, da bi našli komplement njegove 1, moramo obrniti števke danega števila.
Tako je komplement 1 od (10011)2je (01100)2
- 2-jev komplement binarnega števila dobimo tako, da obrnemo števke binarnega števila in nato dodamo 1 najmanj pomembnemu bitu.
Primer: Poiščite komplement dvojke od (1011) 2 .
rešitev:
Dano binarno število je (1011)2
Če želite najti komplement 2, najprej poiščite njegov komplement 1, tj. (0100)2
Zdaj, če dodamo 1 najmanj pomembnemu bitu, dobimo (0101)2
Zato je komplement 2 od (1011)2je (0101)2
Uporaba binarnega številskega sistema
Dvojiški številski sistemi se uporabljajo za različne namene in najpomembnejša uporaba binarnega številskega sistema je,
- Binarni številski sistem se uporablja v vsej digitalni elektroniki za izvajanje različnih operacij.
- Programski jeziki uporabljajo binarni številski sistem za kodiranje in dekodiranje podatkov.
- Binarni številski sistem se uporablja v podatkovnih znanostih za različne namene itd.
Preberi več,
- Binarna formula
- Razlika med decimalnim in binarnim številskim sistemom
Primer binarnega številskega sistema
1. primer: pretvorba decimalnih številk (98) 10 v dvojiško.
rešitev:
Tako binarno število za (98)10je enako (1100010)2
2. primer: pretvorba binarnega števila (1010101) 2 na decimalno število.
rešitev:
Dano binarno število, (1010101)2
= (1 × 20) + (0 × 21) + (1 × 22) + (0 × 23) + (1 × 24) + (0 × 25) + (1 × 26)
= 1 + 0 + 4 + 0 + 16 + 0 + 64
= (85)10
Tako binarno število (1010101)2je enako (85)10v decimalnem sistemu.
Primer 3: Razdeli (11110) 2 avtor (101) 2
rešitev:
Primer 4: Dodaj (11011) 2 in (10100) 2
rešitev:
Torej, (11011)2+ (10100)2= (101111)2
Primer 5: Odštej (11010) 2 in (10110) 2
rešitev:
Torej (11010)2– (10110)2= (00100)2
Primer 6: Pomnoži (1110) 2 in (1001) 2 .
rešitev:
Tako (1110)2× (1001)2= (1111110)2
Pogosta vprašanja o binarnem številskem sistemu
Kaj je binarni številski sistem?
Binarni številski sistem je eden od štirih številskih sistemov, ki se uporablja za predstavitev števil z uporabo samo dveh števk, 0 in 1. V binarnem številskem sistemu se števke imenujejo 'biti'. Binarni številski sistem uporabljajo računalniki za izvajanje različnih izračunov.
Kaj je a B to?
Bit v binarnem številskem sistemu je opredeljen kot posamezna cifra, ki ima vrednost '0' ali '1'.
Kaj je Nibble?
Skupina štirih številk se imenuje Niblle.
Kaj je binarna vrednost 10?
Binarna vrednost 10 je (1010)2
Katere so vrste številskih sistemov?
Obstajajo različne vrste številskih sistemov in nekateri med njimi so,
- Dvojiški številski sistem
- Osmiški številski sistem
- Decimalni številski sistem
- Šestnajstiški številski sistem
Kako izračunati binarna števila?
Dvojiška števila izračunamo iz dicmalnih števil tako, da decimalno število delimo z 2 in preostanek zapišemo. Nato uredimo vse ostanke od najnovejšega do najstarejšega, da dobimo binarno število.
Kako sešteti binarna števila?
Dvojiška števila se dodajajo z uporabo spodnjih formul,
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0 (prenesi 1)






