Binarno drevo je uravnoteženo, če je višina drevesa O(Log n), kjer je n število vozlišč. Na primer, drevo AVL vzdržuje višino O(Log n) tako, da zagotovi, da je razlika med višinama levega in desnega poddrevesa največ 1. Rdeče-črna drevesa vzdržujejo višino O(Log n) tako, da zagotovijo, da je število črnih vozlišč na vsaki poti od korena do lista je enako in da ni sosednjih rdečih vozlišč. Drevesa uravnoteženega binarnega iskanja so dobra glede zmogljivosti, saj zagotavljajo O(log n) časa za iskanje, vstavljanje in brisanje.
Uravnoteženo binarno drevo je binarno drevo, ki upošteva 3 pogoje:
- Višina levega in desnega drevesa za nobeno vozlišče se ne razlikuje za več kot 1.
- Levo poddrevo tega vozlišča je prav tako uravnoteženo.
- Desno poddrevo tega vozlišča je prav tako uravnoteženo.
Posamezno vozlišče je vedno uravnoteženo. Imenujejo ga tudi višinsko uravnoteženo binarno drevo.
Primer :
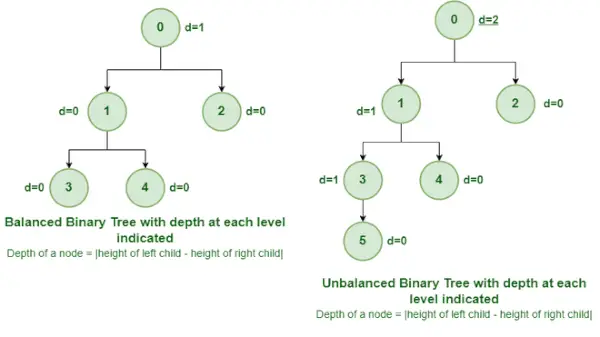
Uravnoteženo in neuravnoteženo binarno drevo
Je vrsta binarnega drevesa, v katerem je razlika med višino levega in desnega poddrevesa za vsako vozlišče 0 ali 1. Na zgornji sliki je korensko vozlišče z vrednostjo 0 neuravnoteženo z globino 2 enoti. .
Uporaba uravnoteženega binarnega drevesa:
- AVL drevesa
- Rdeče črno drevo
- Uravnoteženo binarno iskalno drevo
Prednosti uravnoteženega binarnega drevesa:
- Nedestruktivne posodobitve podpira uravnoteženo binarno drevo z enako asimptotično učinkovitostjo.
- Poizvedbe obsega in ponavljanje v pravem zaporedju so izvedljive z uravnoteženim binarnim drevesom.
