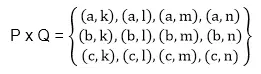Množice pod operacijami unije, presečišča in komplementa izpolnjujejo različne zakone (identitete), ki so navedeni v tabeli 1.
Tabela: Zakon algebre množic
| Idempotentni zakoni | (a) A ∪ A = A | (b) A ∩ A = A |
| Asociativni zakoni | (a) (A ∪ B) ∪ C = A ∪ (B ∪ C) | (b) (A ∩ B) ∩ C = A ∩ (B ∩ C) |
| Komutativni zakoni | (a) A ∪ B = B ∪ A | (b) A ∩ B = B ∩ A |
| Distributivni zakoni | (a) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) | (b) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) |
| De Morganovi zakoni | (a) (A ∪B)c=Ac∩ Bc | (b) (A ∩ B)c=Ac∪ Bc |
| Zakoni o identiteti | (a) A ∪ ∅ = A (b) A ∪ U = U | (c) A ∩ U =A (d) A ∩ ∅ = ∅ |
| Dopolnilni zakoni | (a) A ∪ Ac= U (b) A ∩ Ac= ∅ | (c) Uc= ∅ (d) ∅c= U |
| Involucijski zakon | (a) (Ac)c= A |
Tabela 1 prikazuje zakon algebre množic.
Primer 1: Dokažite idempotentne zakone:
(a) A ∪ A = A
rešitev:
Since, B ⊂ A ∪ B, therefore A ⊂ A ∪ A Let x ∈ A ∪ A ⇒ x ∈ A or x ∈ A ⇒ x ∈ A ∴ A ∪ A ⊂ A As A ∪ A ⊂ A and A ⊂ A ∪ A ⇒ A =A ∪ A. Hence Proved.
(b) A ∩ A = A
rešitev:
Since, A ∩ B ⊂ B, therefore A ∩ A ⊂ A Let x ∈ A ⇒ x ∈ A and x ∈ A ⇒ x ∈ A ∩ A ∴ A ⊂ A ∩ A As A ∩ A ⊂ A and A ⊂ A ∩ A ⇒ A = A ∩ A. Hence Proved.
Primer 2: Dokažite asociativne zakone:
(a) (A ∪ B) ∪ C = A ∪ (B ∪ C)
rešitev:
Let some x ∈ (A'∪ B) ∪ C ⇒ (x ∈ A or x ∈ B) or x ∈ C ⇒ x ∈ A or x ∈ B or x ∈ C ⇒ x ∈ A or (x ∈ B or x ∈ C) ⇒ x ∈ A or x ∈ B ∪ C ⇒ x ∈ A ∪ (B ∪ C). Similarly, if some x ∈ A ∪ (B ∪ C), then x ∈ (A ∪ B) ∪ C. Thus, any x ∈ A ∪ (B ∪ C) ⇔ x ∈ (A ∪ B) ∪ C. Hence Proved.
(b) (A ∩ B) ∩ C = A ∩ (B ∩ C)
rešitev:
Let some x ∈ A ∩ (B ∩ C) ⇒ x ∈ A and x ∈ B ∩ C ⇒ x ∈ A and (x ∈ B and x ∈ C) ⇒ x ∈ A and x ∈ B and x ∈ C ⇒ (x ∈ A and x ∈ B) and x ∈ C) ⇒ x ∈ A ∩ B and x ∈ C ⇒ x ∈ (A ∩ B) ∩ C. Similarly, if some x ∈ A ∩ (B ∩ C), then x ∈ (A ∩ B) ∩ C Thus, any x ∈ (A ∩ B) ∩ C ⇔ x ∈ A ∩ (B ∩ C). Hence Proved.
Primer3: Dokažite komutativne zakone
(a) A ∪ B = B ∪ A
rešitev:
To Prove A ∪ B = B ∪ A A ∪ B = {x: x ∈ A or x ∈ B} = {x: x ∈ B or x ∈ A} (∵ Order is not preserved in case of sets) A ∪ B = B ∪ A. Hence Proved. (b) A ∩ B = B ∩ A
rešitev:
To Prove A ∩ B = B ∩ A A ∩ B = {x: x ∈ A and x ∈ B} = {x: x ∈ B and x ∈ A} (∵ Order is not preserved in case of sets) A ∩ B = B ∩ A. Hence Proved. Primer 4: Dokaži distribucijske zakone
(a) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
rešitev:
To Prove Let x ∈ A ∪ (B ∩ C) ⇒ x ∈ A or x ∈ B ∩ C ⇒ (x ∈ A or x ∈ A) or (x ∈ B and x ∈ C) ⇒ (x ∈ A or x ∈ B) and (x ∈ A or x ∈ C) ⇒ x ∈ A ∪ B and x ∈ A ∪ C ⇒ x ∈ (A ∪ B) ∩ (A ∪ C) Therefore, A ∪ (B ∩ C) ⊂ (A ∪ B) ∩ (A ∪ C)............(i) Again, Let y ∈ (A ∪ B) ∩ (A ∪ C) ⇒ y ∈ A ∪ B and y ∈ A ∪ C ⇒ (y ∈ A or y ∈ B) and (y ∈ A or y ∈ C) ⇒ (y ∈ A and y ∈ A) or (y ∈ B and y ∈ C) ⇒ y ∈ A or y ∈ B ∩ C ⇒ y ∈ A ∪ (B ∩ C) Therefore, (A ∪ B) ∩ (A ∪ C) ⊂ A ∪ (B ∩ C)............(ii) Combining (i) and (ii), we get A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C). Hence Proved
(b) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
rešitev:
To Prove Let x ∈ A ∩ (B ∪ C) ⇒ x ∈ A and x ∈ B ∪ C ⇒ (x ∈ A and x ∈ A) and (x ∈ B or x ∈ C) ⇒ (x ∈ A and x ∈ B) or (x ∈ A and x ∈ C) ⇒ x ∈ A ∩ B or x ∈ A ∩ C ⇒ x ∈ (A ∩ B) ∪ (A ∪ C) Therefore, A ∩ (B ∪ C) ⊂ (A ∩ B) ∪ (A ∪ C)............ (i) Again, Let y ∈ (A ∩ B) ∪ (A ∪ C) ⇒ y ∈ A ∩ B or y ∈ A ∩ C ⇒ (y ∈ A and y ∈ B) or (y ∈ A and y ∈ C) ⇒ (y ∈ A or y ∈ A) and (y ∈ B or y ∈ C) ⇒ y ∈ A and y ∈ B ∪ C ⇒ y ∈ A ∩ (B ∪ C) Therefore, (A ∩ B) ∪ (A ∪ C) ⊂ A ∩ (B ∪ C)............ (ii) Combining (i) and (ii), we get A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∪ C). Hence Proved
Primer 5: Dokaži De Morganove zakone
(a) (A ∪B)<sup>c</sup>=A<sup>c</sup>∩ B<sup>c</sup>
rešitev:
To Prove (A ∪B)<sup>c</sup>=A<sup>c</sup>∩ B<sup>c</sup> Let x ∈ (A ∪B)<sup>c</sup> ⇒ x ∉ A ∪ B (∵ a ∈ A ⇔ a ∉ A<sup>c</sup>) ⇒ x ∉ A and x ∉ B ⇒ x ∉ A<sup>c</sup> and x ∉ B<sup>c</sup> ⇒ x ∉ A<sup>c</sup>∩ B<sup>c</sup> Therefore, (A ∪B)<sup>c</sup> ⊂ A<sup>c</sup>∩ B<sup>c</sup>............. (i) Again, let x ∈ A<sup>c</sup>∩ B<sup>c</sup> ⇒ x ∈ A<sup>c</sup> and x ∈ B<sup>c</sup> ⇒ x ∉ A and x ∉ B ⇒ x ∉ A ∪ B ⇒ x ∈ (A ∪B)<sup>c</sup> Therefore, A<sup>c</sup>∩ B<sup>c</sup> ⊂ (A ∪B)<sup>c</sup>............. (ii) Combining (i) and (ii), we get A<sup>c</sup>∩ B<sup>c</sup> =(A ∪B)<sup>c</sup>. Hence Proved.
(b) (A ∩B)<sup>c</sup> = A<sup>c</sup>∪ B<sup>c</sup>
rešitev:
Let x ∈ (A ∩B)<sup>c</sup> ⇒ x ∉ A ∩ B (∵ a ∈ A ⇔ a ∉ A<sup>c</sup>) ⇒ x ∉ A or x ∉ B ⇒ x ∈ A<sup>c</sup> and x ∈ B<sup>c</sup> ⇒ x ∈ A<sup>c</sup>∪ B<sup>c</sup> ∴ (A ∩B)<sup>c</sup>⊂ (A ∪B)<sup>c</sup>.................. (i) Again, Let x ∈ A<sup>c</sup>∪ B<sup>c</sup> ⇒ x ∈ A<sup>c</sup> or x ∈ B<sup>c</sup> ⇒ x ∉ A or x ∉ B ⇒ x ∉ A ∩ B ⇒ x ∈ (A ∩B)<sup>c</sup> ∴ A<sup>c</sup>∪ B<sup>c</sup>⊂ (A ∩B)<sup>c</sup>.................... (ii) Combining (i) and (ii), we get(A ∩B)<sup>c</sup>=A<sup>c</sup>∪ B<sup>c</sup>. Hence Proved.
Primer 6: Dokažite zakone identitete.
(a) A ∪ ∅ = A
rešitev:
To Prove A ∪ ∅ = A Let x ∈ A ∪ ∅ ⇒ x ∈ A or x ∈ ∅ ⇒ x ∈ A (∵x ∈ ∅, as ∅ is the null set ) Therefore, x ∈ A ∪ ∅ ⇒ x ∈ A Hence, A ∪ ∅ ⊂ A. We know that A ⊂ A ∪ B for any set B. But for B = ∅, we have A ⊂ A ∪ ∅ From above, A ⊂ A ∪ ∅ , A ∪ ∅ ⊂ A ⇒ A = A ∪ ∅. Hence Proved.
(b) A ∩ ∅ = ∅
rešitev:
To Prove A ∩ ∅ = ∅ If x ∈ A, then x ∉ ∅ (∵∅ is a null set) Therefore, x ∈ A, x ∉ ∅ ⇒ A ∩ ∅ = ∅. Hence Proved.
(c) A ∪ U = U
rešitev:
To Prove A ∪ U = U Every set is a subset of a universal set. ∴ A ∪ U ⊆ U Also, U ⊆ A ∪ U Therefore, A ∪ U = U. Hence Proved.
(d) A ∩ U = A
rešitev:
To Prove A ∩ U = A We know A ∩ U ⊂ A................. (i) So we have to show that A ⊂ A ∩ U Let x ∈ A ⇒ x ∈ A and x ∈ U (∵ A ⊂ U so x ∈ A ⇒ x ∈ U ) ∴ x ∈ A ⇒ x ∈ A ∩ U ∴ A ⊂ A ∩ U................. (ii) From (i) and (ii), we get A ∩ U = A. Hence Proved.
Primer7: Dokažite zakone komplementa
(a) A ∪ A<sup>c</sup>= U
rešitev:
To Prove A ∪ A<sup>c</sup>= U Every set is a subset of U ∴ A ∪ A<sup>c</sup> ⊂ U.................. (i) We have to show that U ⊆ A ∪ A<sup>c</sup> Let x ∈ U ⇒ x ∈ A or x ∉ A ⇒ x ∈ A or x ∈ A<sup>c</sup> ⇒ x ∈ A ∪ A<sup>c</sup> ∴ U ⊆ A ∪ A<sup>c</sup>................... (ii) From (i) and (ii), we get A ∪ A<sup>c</sup>= U. Hence Proved.
(b) A ∩ A<sup>c</sup>=∅
rešitev:
As ∅ is the subset of every set ∴ ∅ ⊆ A ∩ A<sup>c</sup>..................... (i) We have to show that A ∩ A<sup>c</sup> ⊆ ∅ Let x ∈ A ∩ A<sup>c</sup> ⇒ x ∈ A and x ∈ A<sup>c</sup> ⇒ x ∈ A and x ∉ A ⇒ x ∈ ∅ ∴ A ∩ A<sup>c</sup> ⊂∅..................... (ii) From (i) and (ii), we get A∩ A<sup>c</sup>=∅. Hence Proved.
(c) U<sup>c</sup>= ∅
rešitev:
Let x ∈ U<sup>c</sup> ⇔ x ∉ U ⇔ x ∈ ∅ ∴ U<sup>c</sup>= ∅. Hence Proved. (As U is the Universal Set).
(d) ∅<sup>c</sup> = U
rešitev:
Let x ∈ ∅<sup>c</sup> ⇔ x ∉ ∅ ⇔ x ∈ U (As ∅ is an empty set) ∴ ∅<sup>c</sup> = U. Hence Proved.
Primer8: Dokažite involucijski zakon
(a) (A<sup>c</sup> )<sup>c</sup> A.
rešitev:
Let x ∈ (A<sup>c</sup> )<sup>c</sup> ⇔ x ∉ A<sup>c</sup>⇔ x ∈ a ∴ (A<sup>c</sup> )<sup>c</sup> =A. Hence Proved.
Dvojnost:
Dualni E∗ od E je enačba, dobljena z zamenjavo vsake pojavitve ∪, ∩, U in ∅ v E z ∩, ∪, ∅ oziroma U. Na primer, dvojnik
(U ∩ A) ∪ (B ∩ A) = A is (∅ ∪ A) ∩ (B ∪ A) = A
Kot načelo dualnosti je zapisano, da če je katera koli enačba E identiteta, potem je njena dvojnost E∗ prav tako identiteta.
Načelo razširitve:
V skladu z načelom razširitve sta dve množici A in B enaki, če in samo če imata enake člene. Enake množice označimo z A=B.
If A= {1, 3, 5} and B= {3, 1, 5}, then A=B i.e., A and B are equal sets. If A= {1, 4, 7} and B= {5, 4, 8}, then A≠ B i.e.., A and B are unequal sets. Kartezični produkt dveh množic:
Kartezični produkt dveh množic P in Q v tem vrstnem redu je množica vseh urejenih parov, katerih prvi člen pripada množici P, drugi člen pa množici Q in je označen s P x Q, tj.
vrsta kopice
P x Q = {(x, y): x ∈ P, y ∈ Q}. primer: Naj bo P = {a, b, c} in Q = {k, l, m, n}. Določite kartezični produkt P in Q.
rešitev: Kartezični produkt P in Q je