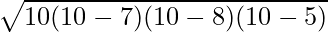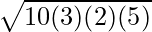Ostrokotni trikotnik je trikotnik, v katerem so vsi koti trikotnikov ostri koti. Trikotnik ima lahko samo en kot kot pravi ali topi kot zaradi lastnosti vsote kotov trikotnika. In zato se trikotnik, ki ima vse tri kote kot ostre kote, tj. kote z vrednostjo, manjšo od 90 stopinj, imenuje ostrokotni trikotnik.

Glede na vrste notranjih kotov trikotnika lahko trikotnik razvrstimo v tri kategorije, trikotnike z ostrim kotom, trikotnike s topim kotom in trikotnike s pravim kotom. Zdaj pa v tem članku podrobno izvemo več o ostrokotnih trikotnikih, njihovih vrstah, lastnostih in drugih.

Kaj je ostrokotni trikotnik?

An ostrokotni trikotnik je definiran kot trikotnik, katerega vsi trije notranji koti so ostri, to pomeni, da je njihova vrednost med 0° in 90°. Glede na vrsto trikotnika so lahko dolžine stranic ostrokotnega trikotnika enake ali neenake. Ostrokotni trikotnik prav tako sledi lastnosti vsote kotov trikotnika.

Spodnja slika je ostrokotni trikotnik, katerega notranji koti so 45°, 35° in 80°. Ker so trije notranji koti manjši od 90°, je dani trikotnik ostrokoten.

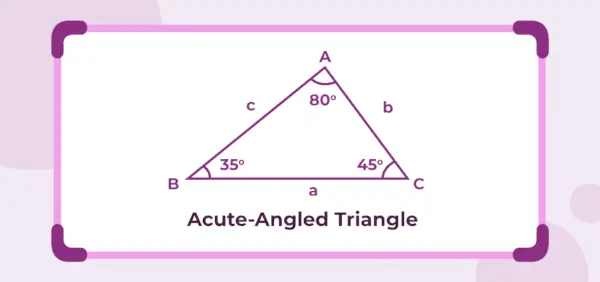
Definicija ostrokotnega trikotnika

Ostrokotne trikotnike definiramo, kot pove ime, kot trikotnike, pri katerih so vsi trije koti trikotnika ostri koti. Stranice v ostrokotnih trikotnikih so lahko enake ali neenake in na podlagi tega se nadalje delijo na tri dele, ki so obravnavani v spodnjem članku,

Vrste ostrokotnih trikotnikov

Ostrokotne trikotnike delimo na tri vrste glede na dolžine stranic trikotnikov:

• Enakostranični ostrokotni trikotnik
• Enakokraki ostrokotni trikotnik
• Scalenski ostrokotni trikotnik

Zdaj pa se o njih podrobneje seznanimo.

Enakostranični ostrokotni trikotnik

Enakostranični ostrokotni trikotnik, imenovan tudi enakostranični trikotnik, je trikotnik, v katerem so vsi koti ostri koti in vsi koti enaki, prav tako sta enaki stranici enakostraničnega ostrokotnega trikotnika. Vsak kot enakostraničnega ostrokotnega trikotnika meri vedno 60°.

povezan seznam v Javi

Enakokraki ostrokotni trikotnik

Enakokraki ostrokotni trikotnik je trikotnik, v katerem so vsi koti ostri koti in sta katera koli dva kota trikotnika in stranica, ki ustreza tema kotoma, enaka. To pomeni, da imamo v enakokrakem ostrokotnem trikotniku dve strani in njuna ustrezna kota enaka.

Scalenski ostrokotni trikotnik

Ostrokotni trikotnik je trikotnik, v katerem so vsi koti ostri koti in nobena kota in nobena stranica nista enaka. To pomeni, da v skalnem ostrokotnem trikotniku nimamo nobenih stranic in nobenih kotov enakih.

Lastnosti ostrokotnega trikotnika

Sledi nekaj pomembnih lastnosti ostrokotnega trikotnika,

• Notranji koti ostrokotnega trikotnika so ostri koti, kar pomeni, da so koti večji od 0°, vendar manjši od 90°.
• Notranji koti ostrokotnih trikotnikov sledijo lastnosti vsote kotov, tj. vsota kotov ostrokotnega trikotnika je 180°.
• Enakostranični trikotnik je vedno ostrokoten, saj vsak notranji kot enakostraničnega trikotnika meri 60°.
• Trikotnik ne more biti hkrati pravokotni in ostrokotni trikotnik.
• Trikotnik ne more biti hkrati ostrokotni in topokotni trikotnik.
• V trikotniku z ostrim kotom je stran, ki je nasprotna najmanjšemu kotu, najmanjša in tudi obratno velja.
• Podobno je stran nasproti največjega kota največja in tudi obratno velja.

Formule ostrokotnega trikotnika

Ploščina in obseg sta dve osnovni formuli trikotnika z ostrim kotom, ki ju obravnavamo spodaj.

Obseg ostrokotnega trikotnika

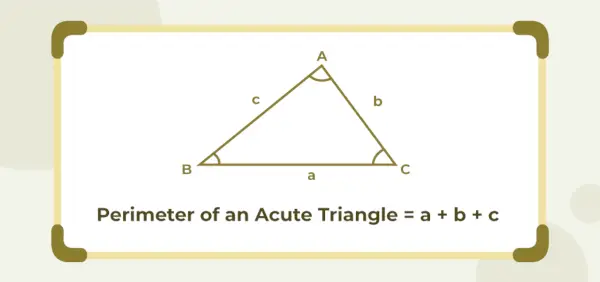
Obseg ostrokotnega trikotnika je enak vsoti njegovih treh dolžin stranic. Če so a, b in c dolžine stranic ostrokotnega trikotnika, potem je njegov obseg podan kot (a + b + c) enote.

Obseg ostrokotnega trikotnika = (a + b + c) enot

Kje a , b , in c so dolžine stranic trikotnika.

Preberi več, Obseg trikotnika

Območje ostrokotnega trikotnika

Območje trikotnika je opredeljeno kot skupni prostor, ki ga omejujejo tri stranice katerega koli trikotnika v dvodimenzionalni ravnini.

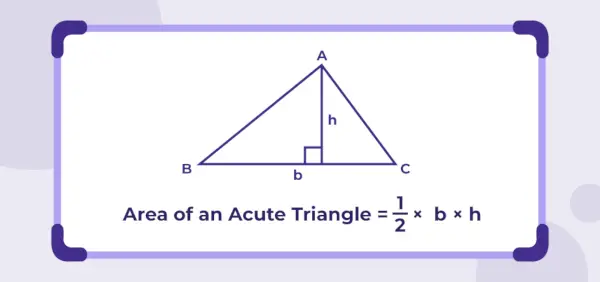
Ploščina ostrokotnega trikotnika = ½ × b × h

Kje,

b je osnovna dolžina in h je višina trikotnika.

Preberi več, Ploščina trikotnika

Območje ostrega trikotnika po Heronovi formuli

Če so podane tri dolžine stranic ostrokotnega trikotnika, lahko njegovo ploščino izračunamo s Heronovo formulo.

Ploščina ostrokotnega trikotnika =

Kje,

s je polobod in s = (a + b + c)/2 , ti , b , in c so dolžine stranic trikotnika.

Preberi več, Heronova formula

Pomembna terminologija trikotnika

Različne terminologije, povezane z ostrokotnim trikotnikom, so:

Okoli centra

Središče kroga, ki poteka mimo treh oglišč trikotnika, se imenuje središče kroga trikotnika. Izračuna se tako, da se vzame presečišče simetrale pravokotnice. Pri trikotniku z ostrim kotom leži središče opisanega kroga vedno znotraj trikotnika.

Središče

Središče kroga, ki se dotika treh stranic trikotnika, imenujemo središče vpisanega trikotnika. Izračuna se tako, da se vzame presečišče simetrale kota. Pri ostrokotnem trikotniku je središče vpisanega vedno znotraj trikotnika.

Centroid

Presečišče median trikotnika imenujemo težišče trikotnika. Pri ostrokotnem trikotniku težišče trikotnika vedno leži znotraj trikotnika.

char v niz v Javi

Ortocenter

Presek višine trikotnika se imenuje ortocenter trikotnika. Pri ostrokotnem trikotniku leži ortocenter trikotnika vedno znotraj trikotnika.

Rešeni primeri o ostrokotnem trikotniku

Primer 1: Kateri od naslednjih kotov lahko tvori ostrokotni trikotnik?

a) 65°, 75°, 50° b) 95°, 40°, 45° c) 70°, 40°, 70° d) 90°, 45°, 45°

rešitev:

Vemo, da so vsi koti v ostrokotnem trikotniku ostri koti, kar pomeni, da je njihova mera manjša od 90 stopinj.

Upoštevajo tudi lastnost vsote kotov trikotnika, tj. vsi njihovi koti seštejejo do 180 stopinj.

a) 65°, 75°, 50°

Tukaj so vsi koti ostri koti, vendar ne sledi lastnosti vsote kotov, zato trikotnik ni mogoč.

65°+ 75°+ 50° = 190° (trikotnik ni mogoč)

b) 95°, 40°, 45°

Tukaj je trikotnik možen, saj sledi lastnosti vsote kotov trikotnika, tj.

95°+ 40°+ 45° = 180

Med opazovanjem kotov trikotnika pa smo našli top kot 95°. Zato trikotnik ni trikotnik z ostrim kotom.

c) 70°,40°,70°

Tukaj je trikotnik možen, saj sledi lastnosti vsote kotov trikotnika, tj.

70°+ 40°+ 70° = 180

In med opazovanjem kotov trikotnika smo ugotovili, da so vsi koti ostri koti. Zato je trikotnik trikotnik z ostrim kotom.

d) 90°, 45°, 45°

Tukaj je trikotnik možen, saj sledi lastnosti vsote kotov trikotnika, tj.

90°+ 45°+ 45° = 180

Med opazovanjem kotov trikotnika pa smo našli pravi kot 90°. Zato trikotnik ni trikotnik z ostrim kotom.

Primer 2: Poiščite obseg ostrokotnega trikotnika XYZ, katerega stranice so XY = 8 enot, YZ = 5 enot in XZ = 9 enot.

css poravnava slik

rešitev:

podano,

Stranice ostrokotnega trikotnika,

• XY(x) = 8 enot
• YZ(y) = 5 enot
• XZ(z) = 9 enot

Vemo, da

Obseg ostrokotnega trikotnika (P) = x + y + z

⇒ P = (8 + 5 + 9) enot

⇒ P = 22 enot

kaj je obj v Javi

Zato je obseg ostrokotnega trikotnika 22 enot.

Primer 3: Poiščite ploščino ostrokotnega trikotnika, katerega višina je 12 enot in osnova 15 enot.

rešitev:

podano,

• Višina trikotnika (h) = 12 enot
• Dolžina osnove trikotnika (b) = 15 enot

Vemo, da

Ploščina trikotnika (A) = ½ × b × h

⇒ A = ½ × 12 × 15

⇒ A = ½ × 180

⇒ A = 90 kvadratnih enot.

Torej je površina danega ostrokotnega trikotnika 90 kvadratnih enot.

Primer 4: Poiščite ploščino ostrokotnega trikotnika, katerega stranice so AB = 5 cm, BC = 7 cm in AC = 8 cm.

rešitev:

podano,

Stranice ostrokotnega trikotnika,

• AB = c = 5 enot
• BC = a = 7 enot
• AC = b = 8 enot

Vemo, da

Površina trikotnika =

⇒ A =

⇒ A =

⇒ A = √(300) kvadratnih cm

⇒ A = 10√3 kvadratnih cm

Torej je ploščina danega ostrokotnega trikotnika 10√3 kvadratnih cm.

Pogosta vprašanja o trikotniku z ostrim kotom

V1: Kaj so ostri koti?

odgovor:

Koti, ki segajo od 0° do 90°, se imenujejo ostri koti. To pomeni, da je najmanjša vrednost ostrega kota večja od 0°, največja vrednost ostrega kota pa večja od 90°.

V2: Kaj je trikotnik z ostrim kotom?

odgovor:

Ostrokotni trikotnik je trikotnik, katerega vsi trije notranji koti so ostri koti, kar pomeni, da je vrednost kota med 0° in 90°.

V3: Ali je enakostranični trikotnik vedno ostrokoten?

odgovor:

Da, enakostranični trikotnik je vedno trikotnik z ostrim kotom. Ostrokotni trikotniki so tisti koti, pri katerih imajo vsi koti ostre kote, v enakostraničnem trikotniku pa so vsi koti 60°, torej ostri koti. Zato je enakostranični trikotnik vedno ostrokoten trikotnik.

V4: Katere so različne vrste trikotnikov z ostrim kotom?

odgovor:

prenesite youtube video vlc

Ostrokotne trikotnike delimo na tri vrste:

• Scalenski ostrokotni trikotnik
• Enakokraki ostrokotni trikotnik
• Enakostranični ostrokotni trikotnik

V5: Kako vedeti, ali je trikotnik ostrokoten?

odgovor:

Trikotnik, katerega notranji koti so manjši od 90°, kar pomeni, da so vsi notranji koti ostri koti, imenujemo ostrokotni trikotnik. Ali je trikotnik ostrokoten, lahko preverimo tako, da preprosto opazujemo kote trikotnika.